Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T04:31:39.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates of Henstock-Kurzweil Poisson Integrals

Published online by Cambridge University Press:  20 November 2018

Erik Talvila
Erik Talvila*
Affiliation:
Department of Mathematics and Statistics, University College of the Fraser Valley, Abbotsford, BC, V2S 7M8 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 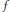$f$ is a real-valued function on 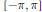$\left[ -\pi ,\,\pi \right]$ that is Henstock-Kurzweil integrable, let 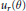${{u}_{r}}(\theta )$ be its Poisson integral. It is shown that 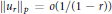${{\left\| {{u}_{r}} \right\|}_{p}}\,=\,o\left( 1/\left( 1-r \right) \right)$ as 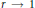$r\,\to \,1$ and this estimate is sharp for 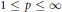$1\,\le \,p\,\le \,\infty $. If $\mu $ is a finite Borel measure and 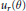${{u}_{r}}(\theta )$ is its Poisson integral then for each 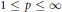$1\,\le \,p\,\le \,\infty $ the estimate 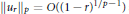${{\left\| {{u}_{r}} \right\|}_{p}}\,=\,O\left( {{\left( 1-r \right)}^{1/p-1}} \right)$ as 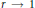$r\,\to \,1$ is sharp. The Alexiewicz norm estimates 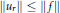$\left\| {{u}_{r}} \right\|\,\le \,\left\| f \right\|$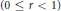$\left( 0\,\le \,r\,<\,1 \right)$ and 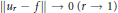$\left\| {{u}_{r}}-f \right\|\,\to 0\left( r\to 1 \right)$ hold. These estimates lead to two uniqueness theorems for the Dirichlet problem in the unit disc with Henstock-Kurzweil integrable boundary data. There are similar growth estimates when 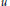$u$ is in the harmonic Hardy space associated with the Alexiewicz norm and when 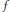$f$ is of bounded variation.

Keywords

26A3931A20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 1 , 01 March 2005 , pp. 133 - 146
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Axler, S., Bourdon, P. and Ramey, W., Harmonic function theory. New York, Springer-Verlag, 2001.Google Scholar
[2] Benedicks, M. and Pfeffer, W. F., The Dirichlet problem with Denjoy-Perron integrable boundary condition. Canad. Math. Bull. 28(1985), 113–119.Google Scholar
[3] Čelidze, V. G. and Džvaršeĭšvili, A. G., The theory of the Denjoy integral and some applications. (trans. Bullen, P. S.), Singapore, World Scientific, 1989.Google Scholar
[4] Folland, G. B., Real analysis. New York, Wiley, 1999.Google Scholar
[5] Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products, (trans. Scripta Technica, ed. Jeffrey, A.), San Diego, Academic Press, 2000.Google Scholar
[6] Shapiro, V. L., The uniqueness of functions harmonic in the interior of the unit disc. Proc. London Math. Soc. 13(1963), 639–652.Google Scholar
[7] Swartz, C., An introduction to functional analysis. New York, Marcel Dekker, 1992.Google Scholar
[8] Swartz, C., Introduction to gauge integrals. Singapore, World Scientific, 2001.Google Scholar
[9] Talvila, E., Henstock-Kurzweil Fourier transforms. Illinois J. Math. 46(2002), 1207–1226.Google Scholar
[10] Talvila, E., Continuity in the Alexiewicz norm, (to appear).Google Scholar
[11] Wolf, F., The Poisson integral. A study in the uniqueness of harmonic functions. Acta. Math. 74(1941), 65–100.Google Scholar