Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T07:29:04.884Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective finiteness of solutions to certain differential and difference equations

Part of: Difference and functional equations Arithmetic algebraic geometry Qualitative theory Difference equations

Published online by Cambridge University Press:  16 February 2021

Patrick Ingram
Patrick Ingram*
Affiliation:
York University, Toronto, Canada
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

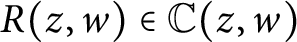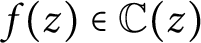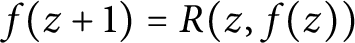For $R(z, w)\in \mathbb {C}(z, w)$ of degree at least 2 in w, we show that the number of rational functions $f(z)\in \mathbb {C}(z)$ solving the difference equation $f(z+1)=R(z, f(z))$ is finite and bounded just in terms of the degrees of R in the two variables. This complements a result of Yanagihara, who showed that any finite-order meromorphic solution to this sort of difference equation must be a rational function. We prove a similar result for the differential equation 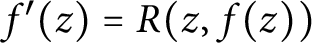$f'(z)=R(z, f(z))$ , building on a result of Eremenko.

Keywords

Difference equationsdifferential equationsrational functionsarithmetic geometry

MSC classification

Primary: 39A22: Growth, boundedness, comparison of solutions
Secondary: 34C11: Growth, boundedness 11G50: Heights
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 1 , March 2022 , pp. 52 - 67
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergweiler, W., On the composition of transcendental entire and meromorphic functions. Proc. Amer. Math. Soc. 123(1995), no. 7, 2151–2153.CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in diophantine geometry. New Mathematical Monographs, 4, Cambridge University Press, Cambridge, 2006.Google Scholar
Eremenko, A., Rational solutions of first-order differential equations. Ann. Acad. Sci. Fenn. Math. 23(1998), no. 1, 181–190.Google Scholar
Feng, R. and Gao, X. S., A polynomial time algorithm for finding rational general solutions of first order autonomous ODEs. J. Symb. Comput. 41(2006), no. 7, 739–762.10.1016/j.jsc.2006.02.002CrossRefGoogle Scholar
Gundersen, G. G., Meromorphic solutions of a differential equation with polynomial coefficients. Comput. Methods Funct. Theory 8(2008), nos. 1–2, 1–14.10.1007/BF03321665CrossRefGoogle Scholar
Gundersen, G. G. and Laine, I., On the meromorphic solutions of some algebraic differential equations. J. Math. Anal. Appl. 111(1985), no. 1, 281–300.10.1016/0022-247X(85)90216-1CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York and Heidelberg, 1977.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H., Diophantine geometry: an introduction. Graduate Texts in Mathematics, 201, Springer-Verlag, New York, 2000.CrossRefGoogle Scholar
Ingram, P., Solutions to difference equations have few defects. Preprint, 2020. arxiv:2011.02975Google Scholar
Mahler, K., On some inequalities for polynomials in several variables. J. Lond. Math. Soc. 37(1962), 341–344.10.1112/jlms/s1-37.1.341CrossRefGoogle Scholar
Malmquist, A. J., Sur les fonctions a un nombre fini de branches définies par les équations différentielles du premier ordre. Acta Math. 36(1913), no. 1, 297–343.10.1007/BF02422385CrossRefGoogle Scholar
Mohon’ko, A. Z., The Nevanlinna characteristics of certain meromorphic functions. Teor. Funkciĭ Funkcional. Anal. i Priložen. 14(1971), 83–87.Google Scholar
Moriwaki, A., Arithmetic height functions over finitely generated fields. Invent. Math. 140(2000), no. 1, 101–142.CrossRefGoogle Scholar
Northcott, D. G., Periodic points on an algebraic variety. Ann. Math. 51(1950), no. 2, 167–177.CrossRefGoogle Scholar
Valiron, G., Sur la dérivée des fonctions algébroïdes. Bull. Soc. Math. France 59(1931), 17–39.CrossRefGoogle Scholar
Yanagihara, N., Meromorphic solutions of some difference equations. Funkcial. Ekvac. 23(1980), no. 3, 309–326.Google Scholar