Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T05:21:42.403Z Has data issue: false hasContentIssue false
  • English
  • Français

A Double Triangle Operator Algebra From SL2(ℝ+)

Published online by Cambridge University Press:  20 November 2018

R. H. Levene
R. H. Levene*
Affiliation:
Pure Mathematics Department, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the 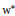${{w}^{*}}$-closed operator algebra 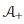${{\mathcal{A}}_{+}}$ generated by the image of the semigroup 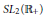$S{{L}_{2}}\left( {{\mathbb{R}}_{+}} \right)$ under a unitary representation 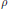$\rho$ of 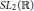$S{{L}_{2}}\left( \mathbb{R} \right)$ on the Hilbert space 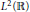${{L}^{2}}\left( \mathbb{R} \right)$. We show that 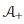${{\mathcal{A}}_{+}}$ is a reflexive operator algebra and 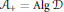${{\mathcal{A}}_{+}}=\text{Alg }\mathcal{D}$ where 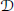$\mathcal{D}$ is a double triangle subspace lattice. Surprisingly, 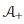${{\mathcal{A}}_{+}}$ is also generated as a 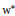${{w}^{*}}$-closed algebra by the image under 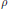$\rho$ of a strict subsemigroup of 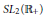$S{{L}_{2}}\left( {{\mathbb{R}}_{+}} \right)$.

Keywords

46K5047L55
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 117 - 126
Copyright
Copyright © Canadian Mathematical Society 2006

Footnotes

The author is supported by an EPSRC grant.

References

[1] Halmos, P. R., Two subspaces. Trans. Amer. Math. Soc. 144(1969), 381–389.Google Scholar
[2] Halmos, P. R., Reflexive lattices of subspaces. J. London Math. Soc. (2) 4(1971), 257–263.Google Scholar
[3] Katavolos, A. and Power, S. C., The Fourier binest algebra. Math. Proc. Cambridge Philos. Soc. 122(1997), 525–539.Google Scholar
[4] Katavolos, A. and Power, S. C., Translation and dilation invariant subspaces of L 2(ℝ) . J. Reine Angew. Math. 552(2002), 101–129.Google Scholar
[5] Lambrou, M. S. and Longstaff, W. E., Finite rank operators leaving double triangles invariant. J. London Math. Soc. (2) 45(1992), 153–168.Google Scholar
[6] Levene, R. H. and Power, S. C., Reflexivity of the translation-dilation algebras on L 2(ℝ) . Internat. J. Math. 14(2003), 1081–1090.Google Scholar
[7] Longstaff, W. E., Nonreflexive double triangles. J. Austral.Math. Soc. Ser. A 35(1983), 349–356.Google Scholar
[8] Sally, P. J. Jr., Harmonic analysis and group representations. In: Studies in Harmonic Analysis, MAA Stud. Math. 13, Math. Assoc. Amer., Washington, D.C., 1976, pp. 224–256.Google Scholar