Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Olsen, James H.
1980.
The Individual Ergodic Theorem for Contractions with Fixed Points.
Canadian Mathematical Bulletin,
Vol. 23,
Issue. 1,
p.
115.
Sato, Ryotaro
1981.
An Extrapolation Theorem for Contractions with Fixed Points.
Canadian Mathematical Bulletin,
Vol. 24,
Issue. 2,
p.
199.
Olsen, James H.
1982.
The Individual Weighted Ergodic Theorem for Bounded Besicovitch Sequences.
Canadian Mathematical Bulletin,
Vol. 25,
Issue. 4,
p.
468.


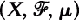 be a finite measure space, and let
be a finite measure space, and let 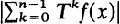 then
then 