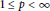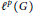Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sawano, Yoshihiro
Tabatabaie, Seyyed Mohammad
and
Shahhoseini, Fatemeh
2021.
Disjoint dynamics of weighted translations on solid spaces.
Topology and its Applications,
Vol. 298,
Issue. ,
p.
107709.
Chen, Chung-Chuan
Tabatabaie, Seyyed Mohammad
and
Mohammadi, Ali
2021.
Disjoint topological transitivity for weighted translations generated by group actions.
Mathematica Slovaca,
Vol. 71,
Issue. 5,
p.
1229.
Chen, Chung-Chuan
2023.
Disjoint topological transitivity for cosine operator functions on weighted Orlicz spaces.
Topology and its Applications,
Vol. 335,
Issue. ,
p.
108563.
Ivković, Stefan
and
Tabatabaie, Seyyed Mohammad
2023.
Disjoint Linear Dynamical Properties of Elementary Operators.
Bulletin of the Iranian Mathematical Society,
Vol. 49,
Issue. 5,