Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T17:05:46.156Z Has data issue: false hasContentIssue false
  • English
  • Français

Diameter, Decomposability, and Minkowski Sums of Polytopes

Part of: Graph theory Polytopes and polyhedra

Published online by Cambridge University Press:  17 December 2018

Antoine Deza  and
Lionel Pournin
Antoine Deza
Affiliation:
Advanced Optimization Laboratory, McMaster University, Hamilton, Ontario, Canada Email: [email protected]
Lionel Pournin
Affiliation:
LIPN, Université Paris 13, Villetaneuse, France Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate how the Minkowski sum of two polytopes affects their graph and, in particular, their diameter. We show that the diameter of the Minkowski sum is bounded below by the diameter of each summand and above by, roughly, the product between the diameter of one summand and the number of vertices of the other. We also prove that both bounds are sharp. In addition, we obtain a result on polytope decomposability. More precisely, given two polytopes 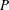$P$ and 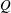$Q$, we show that 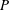$P$ can be written as a Minkowski sum with a summand homothetic to 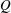$Q$ if and only if 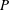$P$ has the same number of vertices as its Minkowski sum with 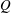$Q$.

Keywords

Minkowski sumpolytopediameterdecomposability

MSC classification

Primary: 05C12: Distance in graphs
Secondary: 52B11: $n$-dimensional polytopes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 741 - 755
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Antoine Deza is partially supported by the Natural Sciences and Engineering Research Council of Canada Discovery Grant program (RGPIN-2015-06163) and Lionel Pournin by the ANR project SoS (Structures on Surfaces), grant number ANR-17-CE40-0033.

References

Adiprasito, K. A. and Sanyal, R., Relative Stanley–Reisner theory and upper bound theorems for Minkowski sums . Publ. Math. Inst. Hautes Études Sci. 124(2016), 99–163. https://doi.org/10.1007/s10240-016-0083-7 Google Scholar
Deza, A., Deza, A., Guan, Z., and Pournin, L., Distance between vertices of lattice polytopes. Optimization letters, to appear.Google Scholar
Deza, A., Manoussakis, G., and Onn, S., Primitive zonotopes . Discrete Comput. Geom. 60(2018), 27–39. https://doi.org/10.1007/s00454-017-9873-z Google Scholar
Fukuda, K., Lecture notes: Polyhedral computation . ETH Zurich, Switzerland, http://www-oldurls.inf.ethz.ch/personal/fukudak/lect/pclect/notes2015/.Google Scholar
Fukuda, K. and Weibel, C., f-Vectors of Minkowski additions of convex polytopes . Discrete Comput. Geom. 37(2007), 503–516. https://doi.org/10.1007/s00454-007-1310-2 Google Scholar
Grünbaum, B., Convex polytopes . Graduate Texts in Mathematics, 221, Springer, 2003. https://doi.org/10.1007/978-1-4613-0019-9 Google Scholar
Kallay, M., Decomposability of polytopes . Israel J. Math. 41(1982), 235–243. https://doi.org/10.1007/BF02771723 Google Scholar
Meyer, W., Indecomposable polytopes . Trans. Amer. Math. Soc. 190(1974), 77–86. https://doi.org/10.2307/1996951 Google Scholar
Przesławski, K. and Yost, D., Decomposability of polytopes . Discrete Comput. Geom. 39(2008), 460–468. https://doi.org/10.1007/s00454-008-9051-4 Google Scholar
Santos, F., A counterexample to the Hirsch conjecture . Ann. of Math. 176(2012), 383–412. https://doi.org/10.4007/annals.2012.176.1.7 Google Scholar
Shephard, G. C., Decomposable convex polyhedra . Mathematika 10(1963), 89–95. https://doi.org/10.1112/S0025579300003995 Google Scholar
Ziegler, G. M., Lectures on polytopes . Graduate Texts in Mathematics, 152, Springer, 1995. https://doi.org/10.1007/978-1-4613-8431-1 Google Scholar