Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-20T07:13:55.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Determining Units in Some Integral Group Rings

Published online by Cambridge University Press:  20 November 2018

E. G. Goodaire ,
E. Jespers  and
M. M. Parmenter
E. G. Goodaire
Affiliation:
Memorial University of Newfoundland, St. John's, Canada, A1C 5S7
E. Jespers
Affiliation:
Memorial University of Newfoundland, St. John's, Canada, A1C 5S7
M. M. Parmenter
Affiliation:
Memorial University of Newfoundland, St. John's, Canada, A1C 5S7
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this brief note, we will show how in principle to find all units in the integral group ring ZG, whenever G is a finite group such that 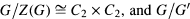and Z(G) each have exponent 2, 3, 4 or 6. Special cases include the dihedral group of order 8, whose units were previously computed by Polcino Milies [5], and the group 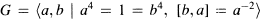discussed by Ritter and Sehgal [6]. Other examples of noncommutative integral group rings whose units have been computed include 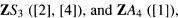, but in general very little progress has been made in this direction. For basic information on units in group rings, the reader is referred to Sehgal [7].

Keywords

16A26
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 33 , Issue 2 , 01 June 1990 , pp. 242 - 246
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Allen, P. J. and Hobby, C., A characterization of units in Z[A4], J. Algebra 66, (1980) 534–543.Google Scholar
2. Allen, P. J. and Hobby, C., A note on the unit group of ZS3 , Proc. A.M.S. 99 (1) (1987), 9–14.Google Scholar
3. Goodaire, E. G. and Parmenter, M. M., Units in alternative loop rings, Israel J. Math. 53 (2) (1986), 209–216.Google Scholar
4. Hughes, I. and Pearson, K. R., The group of units of the integral group ring ZS3, Canad. Math. Bull. 15 (1972), 529–534.Google Scholar
5. Polcino Milies, C. S., The group of units of the integral group ring ZD4, Boletim Soc. Bras. Mat. 4 (2) (1973), 85–92.Google Scholar
6. Ritter, J. and Sehgal, S. K., Construction of units in integral group rings of finite nilpotent groups, Trans. Amer. Math. Soc. to appear 1990.Google Scholar
7. Sehgal, S. K., Topics in Group Rings, Marcel Dekker, New York, 1978.Google Scholar