Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T18:16:57.804Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution Orthogonality and the Jacobi Polynominals

Published online by Cambridge University Press:  20 November 2018

Wm. R. Allaway
Wm. R. Allaway*
Affiliation:
Department of Mathematical Sciences Lakehead University Thunder Bay, Ontario, Canada P7B 5El
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

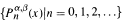Let α and β be any two real numbers and let be the Jacobi polynomial sequences. For any non-zero real number a, 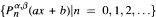is an orthogonal polynomial sequence with respect to convolution if and only if either (i) b = 1, α = 0 and β + 1 is not equal to a negative integer or (ii) b = — 1, β = 0 and α + 1 is not equal to a negative integer.

Keywords

Orthogonal polynomialJacobi PolynominalsOrthogonal Polynominals with respect to convolutionConvolutionThree Term Recursion Relation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 32 , Issue 3 , 01 September 1989 , pp. 298 - 308
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Amerbaev, V. and Zh. Naurzbaev, Polynomials orthogonal with respect to convolution, Izv. Akad. Nauk. Kazan. SSR Ser. Fiz - Mat. Nauk. 3 (1965), 70–78.Google Scholar
2. Brezinski, C., Fade Type Approximation and General Orthogonal Polynomials, (Birkhauser Verlag, Boston) 1980.Google Scholar
3. Chihara, T. S., An Introduction to Orthogonal Polynomials, (Gordon and Beach, New York) 1978.Google Scholar
4. Rainville, E. D., Special Functions, (Macmillan, New York), 1960.Google Scholar