Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T13:00:42.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of Convolution and SIN Groups

Published online by Cambridge University Press:  20 November 2018

Jan Pachl  and
Juris Steprans
Jan Pachl
Affiliation:
Fields Institute, 222 College Street, Toronto, ON M5T 3J1 e-mail: [email protected]
Juris Steprans
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON M3J 1P3 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let the measure algebra of a topological group 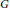$G$ be equipped with the topology of uniform convergence on bounded right uniformly equicontinuous sets of functions. Convolution is separately continuous on the measure algebra, and it is jointly continuous if and only if 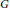$G$ has the 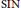$\text{SIN}$ property. On the larger space 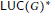$\text{LUC}{{(G)}^{*}}$, which includes the measure algebra, convolution is also jointly continuous if and only if the group has the 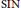$\text{SIN}$ property, but not separately continuous for many non-SIN groups.

Keywords

43A1022A10topological groupSIN propertymeasure algebraconvolution
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 845 - 854
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Berglund, J. F., Junghenn, H. D., and P. Milnes, Analysis on semigroups. Canadian Mathematical Society Series of Monographs and Advanced Texts, John Wiley & Sons Inc., New York, 1989. Google Scholar
[2] Bogachev, V. I., Measure theory. Vol. I, II. Springer-Verlag, Berlin, 2007. http://dx.doi.org/10.1007/978-3-540-34514-5 Google Scholar
[3] Bouziad, A. and J.-P. Troallic, Problems about the uniform structures of topological groups. In: Open Problems in Topology II, Elsevier, Oxford, 2007, pp. 359–366. Google Scholar
[4] Ferri, S. and M. Neufang, On the topological centre of the algebra LUC(G) * for general topological groups. J. Funct. Anal. 244(2007), no. 1,154-171. http://dx.doi.org/10.1016/j.jfa.2006.11.011 Google Scholar
[5] Itzkowitz, G., S. Rothman, H. Strassberg, and Wu, T. S., Characterization of equivalent uniformities in topological groups. Topology Appl. 47(1992), no. 1, 9–34. http://dx.doi.org/10.101 6/01 66-8641 (92)90112- D Google Scholar
[6] Lau, A. T.-M., Continuity of Arens multiplication on the dual space of bounded uniformly continuous functions on locally compact groups and topological semigroups. Math. Proc. Cambridge Philos. Soc. 99(1986), no. 2, 273–283. http://dx.doi.org/10.101 7/S03050041000641 97 Google Scholar
[7] Lau, A. T.-M. and J. Pym, The topological centre of a compactification of a locally compact group. Math. Z. 219(1995), no. 4, 567–579. http://dx.doi.org/10.1007/BF02572381 Google Scholar
[8] Milnes, P., Uniformity and uniformly continuous functions for locally compact groups. Proc. Amer. Math. Soc. 109(1990), no. 2, 567–570. http://dx.doi.org/10.1090/S0002-9939-1 990-1023345-7 Google Scholar
[9] Neufang, M., J. Pachl, and P. Salmi, Uniform equicontinuity, multiplier topology and continuity of convolution. Arch. Math. (Basel) 104(2015), no. 4, 367–376. http://dx.doi.org/10.1007/s00013-015-0726-9 Google Scholar
[10] Pachl, J., Uniform spaces and measures. Fields Institute Monographs, 30, Springer, New York, 2013 (Corrections and supplements at http://www.fields.utoronto.ca/publications/supplements). http://dx.doi.org/10.1007/978-1-4614-5058-0 Google Scholar
[11] Pestov, V., Dynamics of infinite-dimensional groups. University Lecture Series, 40, American Mathematical Society, Providence, RI, 2006. http://dx.doi.org/! 0.1090/ulect/040 Google Scholar
[12] Protasov, I., Functionally balanced groups. (Russian) Mat. Zametki 49(1991), no. 6, 87–91; translation in: Math. Notes 49(1991), 614-616. http://dx.doi.org/10.1007/BF011 56586 Google Scholar
[13] Roelcke, W. and S. Dierolf, Uniform structures on topological groups and their quotients. McGraw-Hill, New York, 1981. Google Scholar
[14] Salmi, P., Joint continuity of multiplication on the dual of the left uniformly continuous functions. Semigroup Forum 80(2010), no. 1,155-163. http://dx.doi.org/10.1007/s00233-009-9189-2 Google Scholar
[15] Villani, C., Optimal transport. Grundlehren der Mathematischen Wissenschaften, 338, Springer-Verlag, Berlin, 2009. http://dx.doi.org/!0.1007/978-3-540-71050-9 Google Scholar