Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T18:18:17.340Z Has data issue: false hasContentIssue false
  • English
  • Français

The Conjugate Function on the Finite Dimensional Torus

Published online by Cambridge University Press:  20 November 2018

Nakhle Asmar
Nakhle Asmar*
Affiliation:
Department of Mathematics and Computer Science, California State University, Long Beach, Long Beach, California 90840
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the group Ta, its group of characters Za, and an arbitrary order P on Za. For x ∊ Za, let sgnpx be 1, - 1 , or 0 according as x € P\{0}, x € (-P)\{0}, or X = 0. For f in Lp(Ta), 1 < p < ∞, it is known that there is a function 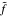in Lp(Ta) such that 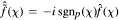for all X in Za. Summability methods for 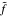are also available. In this paper, we obtain summability methods for 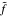that apply for 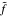in L1(Ta), and we show how various properties of 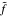can be derived from our construction.

Keywords

43A55
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 32 , Issue 2 , 01 June 1989 , pp. 140 - 148
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Asmar, N. and Edwin Hewitt, Marcel Rieszs theorem on conjugate Fourier series and its descendants. Proceedings of the Analysis conference and workshop held in Singapore, 1986. Edited by T. L. Choy. North-Holland 1988.Google Scholar
2. Berkson, Earl and T.A. Gillespie, The generalized M. Riesz theorem and transference. Pacific J. Math. 120 (2) (1985), 279–288.Google Scholar
3. Calderon, Alberto P., Ergodic theory and translation-invariant operators. Proc. Nat. Aca. Sci. U.S.A., 59 (2) (1968), 855–857.Google Scholar
4. Helson, Henry, Conjugate series and a theorem of Paley. Pacific J. Math. 8 (1958), 437–446.Google Scholar
5. Hewitt, Edwin and Gunter Ritter, Conjugate Fourier series on certain solenoids. Trans. Amer. Math. Soc. 276 (2) (1983), 817–840.Google Scholar
6. Hewitt, Edwin and Kenneth Ross, Abstract harmonic analysis I. Grundlehren der mathematischen Wissenschaften, 115, Second Edition. Berlin, Heidelberg, New York: Springer-Verlag 1979.Google Scholar