Congruence Relationships for Integral Recurrences

Extract

A sequence {u_n}, n=0, 1, 2, 3,… is said to be an integral recurrence of order r if the terms satisfy the equation

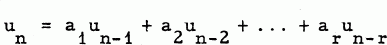
for n=r+1, r+2,…, and a₁, a₂,…, a_r are integers, a_r≠0. In this case we will say that {u_n} satisfies the relation [a₁, a₂,…, a_r]. The sequence {u_n} is uniquely determined when u₁, u₂,…, u_r are given specified values. If u₁, u₂,…, u_r are integers all the terms of {u_n} are integers. The generating function f(t)=u₁t + u₂t²+… takes on the form 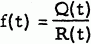where Q(t) depends on the values of u₁, u₂,…, u_r and R(t)=t^r-a₁t^r-1-a₂t^r-2-…-a_r. We will refer to R(t) as the characteristic polynomial of the recurrence.