Article contents
Cancellation of two classes of dirichlet coefficients over Beatty sequences
Published online by Cambridge University Press: 20 April 2021
Abstract
Let 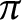 $\pi $
be an automorphic irreducible cuspidal representation of
$\pi $
be an automorphic irreducible cuspidal representation of 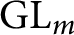 $\mathrm{GL}_{m}$
over
$\mathrm{GL}_{m}$
over 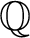 $\mathbb {Q}$
. Denoted by
$\mathbb {Q}$
. Denoted by 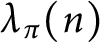 $\lambda _{\pi }(n)$
the nth coefficient in the Dirichlet series expansion of
$\lambda _{\pi }(n)$
the nth coefficient in the Dirichlet series expansion of 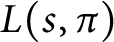 $L(s,\pi )$
associated with
$L(s,\pi )$
associated with 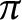 $\pi $
. Let
$\pi $
. Let 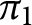 $\pi _{1}$
be an automorphic irreducible cuspidal representation of
$\pi _{1}$
be an automorphic irreducible cuspidal representation of 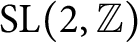 $\mathrm{SL}(2,\mathbb {Z})$
. Denoted by
$\mathrm{SL}(2,\mathbb {Z})$
. Denoted by 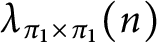 $\lambda _{\pi _{1}\times \pi _{1}}(n)$
the nth coefficient in the Dirichlet series expansion of
$\lambda _{\pi _{1}\times \pi _{1}}(n)$
the nth coefficient in the Dirichlet series expansion of 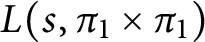 $L(s,\pi _{1}\times \pi _{1})$
associated with
$L(s,\pi _{1}\times \pi _{1})$
associated with  $\pi _{1}\times \pi _{1}$
. In this paper, we study the cancellations of
$\pi _{1}\times \pi _{1}$
. In this paper, we study the cancellations of 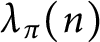 $\lambda _{\pi }(n)$
and
$\lambda _{\pi }(n)$
and 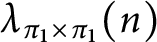 $\lambda _{\pi _{1}\times \pi _{1}}(n)$
over Beatty sequences.
$\lambda _{\pi _{1}\times \pi _{1}}(n)$
over Beatty sequences.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
- 1
- Cited by



