Article contents
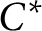 $C^*$-algebra structure on certain Banach algebra products
$C^*$-algebra structure on certain Banach algebra products
Published online by Cambridge University Press: 07 September 2020
Abstract
Let
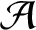 $\mathcal A$
and
$\mathcal A$
and
 $\mathcal B$
be commutative and semisimple Banach algebras and let
$\mathcal B$
be commutative and semisimple Banach algebras and let
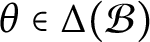 $\theta \in \Delta (\mathcal B)$
. In this paper, we prove that
$\theta \in \Delta (\mathcal B)$
. In this paper, we prove that
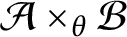 $\mathcal A\times _{\theta }\mathcal B$
is a type I-BSE algebra if and only if
$\mathcal A\times _{\theta }\mathcal B$
is a type I-BSE algebra if and only if
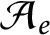 ${\mathcal A}_e$
and
${\mathcal A}_e$
and
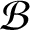 $\mathcal B$
are so. As a main application of this result, we prove that
$\mathcal B$
are so. As a main application of this result, we prove that
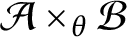 $\mathcal A\times _{\theta }\mathcal B$
is isomorphic with a
$\mathcal A\times _{\theta }\mathcal B$
is isomorphic with a
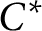 $C^*$
-algebra if and only if
$C^*$
-algebra if and only if
 ${\mathcal A}_e$
and
${\mathcal A}_e$
and
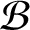 $\mathcal B$
are isomorphic with
$\mathcal B$
are isomorphic with
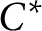 $C^* $
-algebras. Moreover, we derive related results for the case where
$C^* $
-algebras. Moreover, we derive related results for the case where
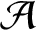 $\mathcal A$
is unital.
$\mathcal A$
is unital.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 1
- Cited by




