Boundedness From Below of Multiplication Operators Between α-Bloch Spaces

Abstract

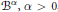In this paper, the boundedness from below of multiplication operators between $\alpha$-Bloch spaces ${{B}^{\alpha }},\,\alpha \,>\,0$, on the unit disk 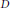$D$ is studied completely. For a bounded multiplication operator 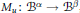${{M}_{u}}\,:\,{{B}^{\alpha }}\,\to \,{{B}^{\beta }}$, defined by 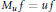${{M}_{u}}f\,=\,uf$ for 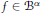$f\,\in \,{{B}^{\alpha }}$, we prove the following result:

(i) If 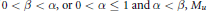$0<\beta <\alpha ,\,\text{or}\,\text{0}<\alpha \le \text{1}\,\text{and}\,\alpha <\beta \text{,}\,{{M}_{u}}$ is not bounded below;

(ii) if 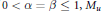$0\,<\,\alpha \,=\,\beta \,\le \,1,\,{{M}_{u}}$ is bounded below if and only if lim 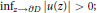${{\inf }_{z\to \partial D}}\,\left| u\left( z \right) \right|\,>\,0;$

(iii) if 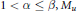$1\,<\,\alpha \,\le \,\beta ,\,{{M}_{u}}$ is bounded below if and only if there exist a 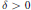$\delta \,>\,0$ and a positive 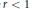$r\,<\,1$ such that for every point 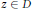$z\,\in \,D$ there is a point 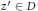${{z}^{'}}\,\in \,D$ with the property 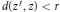$d\left( {{z}^{'}},\,z \right)\,<\,r$ and 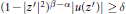${{\left( 1\,-\,{{\left| {{z}^{'}} \right|}^{2}} \right)}^{\beta -\alpha }}\left| u\left( {{z}^{'}} \right) \right|\,\ge \,\delta$, where 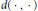$d\left( \cdot ,\,\cdot \right)$ denotes the pseudo-distance on $D$.