Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T03:49:10.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary Behavior of Solutions of the Helmholtz Equation

Published online by Cambridge University Press:  20 November 2018

Kentaro Hirata
Kentaro Hirata*
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the boundary behavior of solutions of the Helmholtz equation in 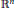${{\mathbb{R}}^{n}}$. In particular, we give a Littlewood-type theorem to show that the approach region introduced by Korányi and Taylor (1983) is best possible.

Keywords

31B2535J05boundary behaviorHelmholtz equation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 4 , 01 December 2009 , pp. 555 - 563
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Aikawa, H., Harmonic functions having no tangential limits. Proc. Amer. Math. Soc. 108(1990), no. 2, 457–464.Google Scholar
[2] Aikawa, H., Harmonic functions and Green potentials having no tangential limits. J. London Math. Soc. (2) 43(1991), no. 1, 125–136.Google Scholar
[3] Berman, R. and Singman, D., Boundary behavior of positive solutions of the Helmholtz equation and associated potentials. Michigan Math. J. 38(1991), no. 3, 381–393.Google Scholar
[4] Brawn, F. T., The Martin boundary of Rn ×]0, 1[. J. London Math. Soc. (2) 5(1972), 59–66.Google Scholar
[5] Fatou, P., Séries trigonométriques et séries de Taylor. Acta Math. 30(1906), no. 1, 335–400.Google Scholar
[6] Gowrisankaran, K. and Singman, D., Thin sets and boundary behavior of solutions of the Helmholtz equation. Potential Anal. 9(1998), no. 4, 383–398.Google Scholar
[7] Hirata, K., Sharpness of the Korányi approach region. Proc. Amer.Math. Soc. 133(2005), no. 8, 2309–2317.Google Scholar
[8] Korányi, A., Harmonic functions on Hermitian hyperbolic space. Trans. Amer. Math. Soc. 135(1969), 507–516.Google Scholar
[9] Korányi, A. and Taylor, J. C., Fine convergence and parabolic convergence for the Helmholtz equation and the heat equation. Illinois J. Math. 27(1983), no. 1, 77–93.Google Scholar
[10] Littlewood, J. E., On a theorem of Fatou. J. London Math. Soc. 2(1927), 172–176.Google Scholar
[11] Nagel, A. and Stein, E. M., On certain maximal functions and approach regions. Adv. in Math. 54(1984), no. 1, 83–106.Google Scholar
[12] Sueiro, J., On maximal functions and Poisson–Szegö integrals. Trans. Amer. Math. Soc. 298(1986), no. 2, 653–669.Google Scholar