Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-08T16:02:52.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Best Possible Nets in a Normed Linear Space1

Published online by Cambridge University Press:  20 November 2018

L. L. Keener
L. L. Keener*
Affiliation:
Summer Research Institute Canadian Mathematical Congress, Dalhousie University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we examine the question of the existence of a best possible N-net for a bounded set in a normed linear space. A sufficient condition for existence is given which leads to easy proofs of some of the standard results. The pertinent reference here is the paper by Garkavi [1].

Let E be a normed linear space and let M be a bounded set in E. Any system of N points in E will be called an N-net. For a given M and the net SN = {y1, y2,…, yN} define

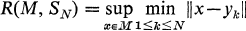
and

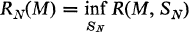
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 45 - 48
Copyright
Copyright © Canadian Mathematical Society 1975

Footnotes

(1)

Supported by National Research Council Grant A8755 and the Canadian Mathematical Congress Summer Research Institute.

References

1. Garkavi, A. L., The best possible net and the best possible cross-section of a set in a normed space. Izv. Akad. Nauk SSSR Ser. Mat. 26 (1962), 87–106; Amer. Math. Soc. Transi., Ser. 2, 39(1964), 111-132.Google Scholar
2. Kelley, J. L., General Topology, D. Van Nostrand Company, Inc., Princeton, New Jersey (1955).Google Scholar