Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T05:37:25.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Assouad–Nagata Dimension of Wreath Products of Groups

Published online by Cambridge University Press:  20 November 2018

N. Brodskiy ,
J. Dydak  and
U. Lang
N. Brodskiy
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, TN 37996, USA e-mail: [email protected]@math.utk.edu
J. Dydak
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, TN 37996, USA e-mail: [email protected]@math.utk.edu
U. Lang
Affiliation:
Eidgen Technische Hochschule Zentrum, CH-8092 Zürich, Switzerland [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the wreath product 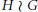$H\,\wr \,G$, where 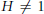$H\,\ne \,1$ is finite and $G$ is finitely generated. We show that the Assouad–Nagata dimension 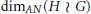${{\dim}_{AN}}\left( H\,\wr \,G \right)$ of 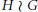$H\,\wr \,G$ depends on the growth of $G$ as follows: if the growth of $G$ is not bounded by a linear function, then 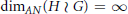${{\dim}_{AN}}\left( H\,\wr \,G \right)\,=\,\infty$; otherwise ${{\dim}_{AN}}\left( H\,\wr \,G \right)\,=\,{{\dim}_{AN}}\left( G \right)\,\le \,1$.

Keywords

54F4555M1054C65Assouad–Nagata dimensionasymptotic dimensionwreath productgrowth of groups
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 245 - 253
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The second-named author was partially supported by the Center for Advanced Studies in Mathematics at Ben Gurion University of the Negev (Beer-Sheva, Israel).

References

[1] Bass, H., The degree of polynomial growth of finitely generated nilpotent groups. Proc. London Math. Soc. (3) 25 (1972), 603–614. http://dx.doi.org/10.1112/plms/s3-25.4.603 CrossRefGoogle Scholar
[2] Brodskiy, N., Dydak, J., Higes, J., and Mitra, A., Assouad-Nagata dimension via Lipschitz extensions. Israel J. Math. 171(2009), 405–423. http://dx.doi.org/10.1007/s11856-009-0056-3 CrossRefGoogle Scholar
[3] Brodskiy, N., Dydak, J., Levin, M., and Mitra, A., A Hurewicz theorem for the Assouad-Nagata dimension. J. Lond. Math. Soc. (2) 77(2008), no. 3, 741–756. http://dx.doi.org/10.1112/jlms/jdn005 CrossRefGoogle Scholar
[4] Cleary, S. and Taback, J., Dead end words in lamplighter groups and other wreath products. Q. J. Math. 56(2005), no. 2, 165–178. http://dx.doi.org/10.1093/qmath/hah030 CrossRefGoogle Scholar
[5] Dranishnikov, A. N., Groups with a polynomial dimension growth. Geom. Dedicata 119(2006), 1–15. http://dx.doi.org/10.1007/s10711-005-9026-z CrossRefGoogle Scholar
[6] Dydak, J. and Higes, J., Asymptotic cones and Assouad-Nagata dimension. Proc. Amer. Math. Soc. 136(2008), no. 6, 2225–2233. http://dx.doi.org/10.1090/S0002-9939-08-09149-1 Google Scholar
[7] Engelking, R., Dimension theory. North-Holland Mathematical Library, 19, North-Holland Publishing Co., Amsterdam-Oxford-New York; PWN–Polish Scientific Publishers, Warsaw, 1978.Google Scholar
[8] Erschler, A., On isoperimetric profiles of finitely generated groups. Geom. Dedicata 100(2003), 157–171. http://dx.doi.org/10.1023/A:1025849602376 CrossRefGoogle Scholar
[9] Gal, S. R., Asymptotic dimension and uniform embeddings. Groups Geom. Dyn. 2(2008), no. 1, 63–84.CrossRefGoogle Scholar
[10] Gromov, M., Groups of polynomial growth and expanding maps. Inst. Hautes Études Sci. Publ. Math. No. 53(1981), 53–73.CrossRefGoogle Scholar
[11] Gromov, M., Asymptotic invariants for infinite groups.In: Geometric group theory, vol. 2, London Math. Soc. Lecture Note Ser., 182, Cambridge University Press, Cambridge, 1993, pp. 1–295.Google Scholar
[12] de la Harpe, P., Topics in geometric group theory. Chicago Lectures in Mathematics, University of Chicago Press, Chicago, IL, 2000.Google Scholar
[13] Lang, U. and Schlichenmaier, T., Nagata dimension, quasisymmetric embeddings, and Lipschitz extensions. Int. Math. Res. Not. 2005, no. 58, 3625–3655.Google Scholar
[14] Kapovich, M., Lectures on geometric group theory. preprint (as of September 28, 2005). https://www.math.ucdavis.edu/_kapovich/EPR/kapovichdrutu.pdf. Google Scholar
[15] Nowak, P.W., On exactness and isoperimetric profiles of discrete groups.J. Funct. Anal. 243 (2007), no. 1, 323–344. http://dx.doi.org/10.1016/j.jfa.2006.10.011 Google Scholar
[16] Smith, J., On asymptotic dimension of countable abelian groups. Topology Appl. 153 (2006), no. 12, 2047–2054. http://dx.doi.org/10.1016/j.topol.2005.07.011 CrossRefGoogle Scholar