Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T17:15:20.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Additive Riemann–Hilbert Problem in Line Bundles Over ℂℙ1

Published online by Cambridge University Press:  20 November 2018

Roman J. Dwilewicz
Roman J. Dwilewicz*
Affiliation:
Department of Mathematics and Statistics, University of Missouri, Rolla, MO 65409, U.S.A.and Institute of Mathematics, Polish Academy of Sciences, Śniadeckich 8, P.O. Box 21, 00-956 Warsaw, Poland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we consider 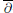$\bar{\partial }$-problem in line bundles over complex projective space 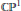$\mathbb{C}{{\mathbb{P}}^{1}}$ and prove that the equation can be solved for (0, 1) forms with compact support. As a consequence, any Cauchy-Riemann function on a compact real hypersurface in such line bundles is a jump of two holomorphic functions defined on the sides of the hypersurface. In particular, the results can be applied to 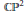$\mathbb{C}{{\mathbb{P}}^{2}}$ since by removing a point from it we get a line bundle over 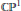$\mathbb{C}{{\mathbb{P}}^{1}}$.

Keywords

32F2014F0532C16∂̄-problemcohomology groupsline bundles
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 72 - 81
Copyright
Copyright © Canadian Mathematical Society 2006

References

[AH] Andreotti, A. and Hill, C. D., E. E. Levi convexity and the Hans Lewy problem. Part I: Reduction to vanishing theorems. Ann. Scuola Norm. Sup. Pisa (3) 26(1972), 325–363.Google Scholar
[DM] Dwilewicz, R. and Merker, J., On the Hartogs–Bochner phenomenon for CR functions in P 2ℂ . Proc.Amer. Math. Soc. 130(2002), 1975–1980.Google Scholar
[GH] Griffiths, P. and Harris, J., Principles of Algebraic Geometry. John Wiley, New York, 1978.Google Scholar
[Gu] Gunning, R. C., Lectures on Riemann surfaces. Princeton University Press, Princeton, NJ, 1966.Google Scholar
[L] Laurent-Thiébaut, C., Phénomène de Hartogs-Bochner dans les variétés CR. In: Topics in Complex Analysis, Banach Center Publications 31, Warszawa, 1995, pp. 233–247.Google Scholar
[N] Narasimhan, R., Complex Analysis in One Variable. Birkhäuser Boston, Boston, MA, 1985.Google Scholar
[S1] Sarkis, F., CR meromorphic extension and the nonembeddability of the Andreotti-Rossi CR structure in the projective space. Internat. J. Math. 10(1999), 897–915.Google Scholar
[S2] Sarkis, F., Hartogs-Bochner type theorem in projective space. Ark. Mat. 41(2003), 151–163.Google Scholar