Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T18:19:30.851Z Has data issue: false hasContentIssue false
  • English
  • Français

Triviality Properties of Principal Bundles on Singular Curves. II

Part of: Curves Families, fibrations

Published online by Cambridge University Press:  24 January 2020

P. Belkale  and
N. Fakhruddin
P. Belkale
Affiliation:
Department of Mathematics, University of North Carolina, Chapel Hill, NC 27599, USA Email: [email protected]
N. Fakhruddin
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400005, India Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 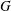$G$ a split semi-simple group scheme and 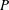$P$ a principal 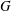$G$-bundle on a relative curve $X\rightarrow S$, we study a natural obstruction for the triviality of 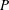$P$ on the complement of a relatively ample Cartier divisor $D\subset X$. We show, by constructing explicit examples, that the obstruction is nontrivial if 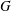$G$ is not simply connected, but it can be made to vanish by a faithfully flat base change, if 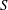$S$ is the spectrum of a dvr (and some other hypotheses). 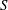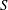The vanishing of this obstruction is shown to be a sufficient condition for étale local triviality if $S$ is a smooth curve, and the singular locus of $X-D$ is finite over $S$.

Keywords

principal bundlesingular curveobstructions to triviality

MSC classification

Primary: 14D20: Algebraic moduli problems, moduli of vector bundles
Secondary: 14H60: Vector bundles on curves and their moduli 14H20: Singularities, local rings
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 423 - 433
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barth, W. P., Hulek, K., Peters, C. A. M., and Van de Ven, A., Compact complex surfaces, Second ed., Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A, Springer-Verlag, Berlin, 2004.CrossRefGoogle Scholar
Beauville, A. and Laszlo, Y., Un lemme de descente. C. R. Acad. Sci. Paris Sér. I Math. 320(1995), no. 3, 335–340.Google Scholar
Belkale, P. and Fakhruddin, N., Triviality properties of principal bundles on singular curves. Algebr. Geom. 6(2019), 234–259. https://doi.org/10.14231/AG-2019-012CrossRefGoogle Scholar
Deligne, P., Milne, J. S., Ogus, A., and Shih, K.-y., Hodge cycles, motives, and Shimura varieties. Lecture Notes in Mathematics, 900, Springer, Berlin–New York, 1982.CrossRefGoogle Scholar
Drinfeld, V. G. and Simpson, C., B-structures on G-bundles and local triviality. Math. Res. Lett. 2(1995), no. 6, 823–829. https://doi.org/10.4310/MRL.1995.v2.n6.a13CrossRefGoogle Scholar
Faltings, G., A proof for the Verlinde formula. J. Algebraic Geom. 3(1994), 347–374.Google Scholar
Grothendieck, A., Le groupe de Brauer. II. Théorie cohomologique. In: Dix Exposés sur la Cohomologie des Schémas. Adv. Stud. Pure Math., 3, North-Holland, Amsterdam; Masson, Paris, 1968, pp. 67–87.Google Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer, New York–Heidelberg, 1977.CrossRefGoogle Scholar
Lipman, J., Desingularization of two-dimensional schemes. Ann. Math. (2) 107(1978), 151–207.CrossRefGoogle Scholar
Solis, P., A wonderful embedding of the loop group. Adv. Math. 313(2017), 689–717. https://doi.org/10.1016/j.aim.2016.10.016CrossRefGoogle Scholar
Solis, P., Nodal uniformization of G-bundles. 2016. arxiv:1608.05681Google Scholar