Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T18:30:56.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-convex Optimization via Strongly Convex Majorization-minimization

Part of: Integral equations, integral transforms

Published online by Cambridge University Press:  10 December 2019

Azita Mayeli
Azita Mayeli*
Affiliation:
Department of Mathematics, The City University of New York, USA Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we introduce a class of nonsmooth nonconvex optimization problems, and we propose to use a local iterative minimization-majorization (MM) algorithm to find an optimal solution for the optimization problem. The cost functions in our optimization problems are an extension of convex functions with MC separable penalty, which were previously introduced by Ivan Selesnick. These functions are not convex; therefore, convex optimization methods cannot be applied here to prove the existence of optimal minimum point for these functions. For our purpose, we use convex analysis tools to first construct a class of convex majorizers, which approximate the value of non-convex cost function locally, then use the MM algorithm to prove the existence of local minimum. The convergence of the algorithm is guaranteed when the iterative points 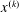$x^{(k)}$ are obtained in a ball centred at 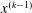$x^{(k-1)}$ with small radius. We prove that the algorithm converges to a stationary point (local minimum) of cost function when the surregators are strongly convex.

Keywords

Cost functionlocal majorizer and minimizersurregatorMoreau envelopeinfimal convolutionconvex functionstationary point

MSC classification

Primary: 65R32: Inverse problems
Secondary: 90C26: Nonconvex programming, global optimization
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 726 - 737
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R. G. Baraniuk, E. Candes, M. Elad, and Y. Ma, eds., Special issue on applications of sparse representation and compressive sensing. Proc. IEEE 98(June 2010), 6.CrossRefGoogle Scholar
Bauschke, H. H. and Combettes, P. L., Convex analysis and monotone operator theory in Hilbert spaces. In: CMS books in mathematics/Ouvrages de Mathématiques de la SMC. Springer, New York, 2011. https://doi.org/10.1007/978-1-4419-9467-7Google Scholar
O’Brien, S., Sinclair, A. N., and Kramer, S. M., Recovery of a sparse spike time series by L 1 norm deconvolution. IEEE Trans. Signal Process. 42(December 1994), 12, 3353–3365.CrossRefGoogle Scholar
Bruckstein, A., Donoho, D., and Elad, M., From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Rev. 51(2009), 34–81. https://doi.org/10.1137/060657704CrossRefGoogle Scholar
Candes, E. J., Wakin, M. B., and Boyd, S., Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 14(2008), 877–905. https://doi.org/10.1007/s00041-008-9045-xCrossRefGoogle Scholar
Chartrand, R., Sidky, E.Y., and Pan, X., Nonconvex compressive sensing for X-ray CT: an algorithm comparison. In: 2013 Asilomar conference on signals, systems and computers. IEEE, 2013, pp. 665–669.CrossRefGoogle Scholar
Chen, S. S., Donoho, D. L., and Saunders, M. A., Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 20(1999), 33–61. https://doi.org/10.1137/S1064827596304010CrossRefGoogle Scholar
Claerbout, J. F. and Muir, F., Robust modeling of erratic data. Geophysics 38(1973), 826–844.CrossRefGoogle Scholar
Daubechies, I., DeVore, R., Fornasier, M., and Gunturk, C., Iteratively reweighted least squares minimization for sparse recovery. Comm. Pure Appl. Math. 63(2010), 1–38. https://doi.org/10.1002/cpa.20303CrossRefGoogle Scholar
Figueiredo, M., Bioucas-Dias, J., and Nowak, R., Majorization-minimization algorithms for wavelet-based image restoration. IEEE Trans. Image Process. 16(2007), 2980–2991. https://doi.org/10.1109/TIP.2007.909318CrossRefGoogle ScholarPubMed
Gasso, G., Rakotomamonjy, A., and Canu., S., Recovering sparse signals with a certain family of nonconvex penalties and DC programming. IEEE Trans. Signal Process. 57(2009), 4686–4698. https://doi.org/10.1109/TSP.2009.2026004CrossRefGoogle Scholar
Gholami, A. and Hosseini, S. M., A general framework for sparsity-based denoising and inversion. IEEE Trans. Signal Process. 59(2011), 11, 5202–5211. https://doi.org/10.1109/TSP.2011.2164074CrossRefGoogle Scholar
Hastie, T., Tibshirani, R., and Friedman, J. H., The elements of statistical learning. In: Data mining, inference, and prediction, 2nd ed., Springer Series in Statistics, Springer, New York, 2009. https://doi.org/10.1007/978-0-387-84858-7Google Scholar
Lange, K., Chi, E. C., and Zhou, H., A brief survey of modern optimization for statisticians. Int. Stat. Rev. 82(2014), 46–70. https://doi.org/10.1111/insr.12022CrossRefGoogle ScholarPubMed
Lang, K., Optimization, 2nd ed., Springer Texts in Statistics, 95, Springer, New York, 2013. https://doi.org/10.1007/978-1-4614-5838-8CrossRefGoogle Scholar
Lanza, A., Morigi, S., Selesnick, I., and Sgallari, F., Nonconvex nonsmooth optimization via convex-nonconvex majorization-minimization. Numer. Math. 136(2017), 343–381. https://doi.org/10.1007/s00211-016-0842-xCrossRefGoogle Scholar
Malioutov, D. and Aravkin, A., Iterative log thresholding. In: 2014 IEEE International conference on acoustics, speech and signal processing (ICASSP). IEEE, 2014, pp. 7198–7202.CrossRefGoogle Scholar
Mairal, J., Optimization with first-order surrogate functions. In: ICML 2013-International conference on machine learning, June 2013, JMLR proceedings, Atlanta, USA. ICML, 2013, pp. 783–791.Google Scholar
Selesnick, I., Sparse regularization via convex analysis. IEEE Trans. Signal Process. 65(2017), 4481–4494. https://doi.org/10.1109/TSP.2017.2711501CrossRefGoogle Scholar
Selesnick, I., Total variation denoising via the Moreau envelope. IEEE Signal Processing Letters 24(2017), 216–220.CrossRefGoogle Scholar
Starck, J. L., Starck, J.-L., Murtagh, F., and Fadili, J., Sparse image and signal processing: Wavelets and related geometric multiscale analysis. Cambridge University Press, New York, 2015. https://doi.org/10.1017/CBO9781316104514CrossRefGoogle Scholar
Taylor, H. L., Banks, S. C., and McCoy, J. F., Deconvolution with the l1 norm. Geophysics 44(1979), 1, 39–52.10.1190/1.1440921CrossRefGoogle Scholar
Tibshirani, R., Regression shrinkage and selection via the lasso. Technical report, University of Toronto, 1994.Google Scholar
Xu, Z., Chang, X., Xu, F., and Zhang., H., L 1/2 regularization: A thresholding representation theory and a fast solver. IEEE T. Neur. Net. Learn. 23(2012), 1013–1027.Google Scholar
Yin, P., Lou, Y., He, Q., and Xin, J., Minimization of ℓ 1-2 for compressed sensing. SIAM J. Sci. Comput. 37(2015), A536–A563. https://doi.org/10.1137/140952363CrossRefGoogle Scholar
Zeng, J., Lin, S., Wang, Y., and Xu, Z., L 1/2 regularization: Convergence of iterative half thresholding algorithm. IEEE Trans. Signal Process. 62(2014), 2317–2329. https://doi.org/10.1109/TSP.2014.2309076CrossRefGoogle Scholar