Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhang, Xuemei
and
Yang, Yuyao
2023.
Necessary and sufficient conditions for the existence of entire subsolutions to p-k-Hessian equations.
Nonlinear Analysis,
Vol. 233,
Issue. ,
p.
113299.
Kan, Shikun
and
Zhang, Xuemei
2023.
Entire positive p-k-convex radial solutions to p-k-Hessian equations and systems.
Letters in Mathematical Physics,
Vol. 113,
Issue. 1,
Feng, Meiqiang
2023.
Eigenvalue problems for singular p-Monge-Ampère equations.
Journal of Mathematical Analysis and Applications,
Vol. 528,
Issue. 2,
p.
127538.
Feng, Meiqiang
and
Zhang, Xuemei
2023.
The existence of infinitely many boundary blow-up solutions to the p-k-Hessian equation.
Advanced Nonlinear Studies,
Vol. 23,
Issue. 1,
Feng, Meiqiang
and
Lu, Yichen
2024.
Existence and asymptotic behavior of nontrivial p-k-convex radial solutions for p-k-Hessian equations.
Letters in Mathematical Physics,
Vol. 114,
Issue. 4,
Wan, Haitao
and
Shi, Yongxiu
2024.
Sharp conditions for the existence of infinitely many positive solutions to $ q $-$ k $-Hessian equation and systems.
Electronic Research Archive,
Vol. 32,
Issue. 8,
p.
5090.
Ding, Zhaoyang
and
Mi, Ling
2024.
Radial Solutions for p-k-Hessian Equations and Systems with Gradient Term.
Journal of Nonlinear Mathematical Physics,
Vol. 31,
Issue. 1,
Feng, Meiqiang
2024.
Positive Radial Solutions to the Double Singular $$k_i$$-Hessian System: Existence, Multiplicity and Dependence on a Parameter.
Communications in Mathematics and Statistics,
Bao, Jiguang
Liu, Zixiao
and
Wang, Cong
2024.
Existence of Entire Solutions to the Lagrangian Mean Curvature Equations in Supercritical Phase.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 5,
Gao, Zhenghuan
2024.
Uniqueness theorem for negative solutions of fully nonlinear elliptic equations in a ball.
Nonlinear Analysis,
Vol. 242,
Issue. ,
p.
113495.
Mi, Ling
and
Ji, YangYang
2024.
On the existence of radially symmetric solutions to p-k-Hessian equations and systems.
Analysis and Mathematical Physics,
Vol. 14,
Issue. 4,
Bai, Zhanbing
and
Yang, Zedong
2025.
On
p
-
k
-convex solutions for the
p
-
k
-Hessian system with the gradient term
.
Quaestiones Mathematicae,
Vol. 48,
Issue. 1,
p.
91.
Feng, Meiqiang
2025.
Existence of countably many p-k-convex solutions for p-k-Hessian equations and systems.
Annals of Functional Analysis,
Vol. 16,
Issue. 2,
Jiang, Feida
Ji, Jingwen
and
Li, Mengni
2025.
Necessary and sufficient conditions on entire solvability for real $$(n-1)$$ Monge–Ampère equation.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 204,
Issue. 2,
p.
447.
Wan, Haitao
2025.
Sharp asymptotic expansions of entire large solutions to a class of k-Hessian equations with weights.
Advances in Nonlinear Analysis,
Vol. 14,
Issue. 1,
Zhang, Xuemei
and
Li, Guoyuan
2025.
Nontrivial p-$$k_i$$-convex radial solutions for p-$$k_i$$-Hessian systems: existence and asymptotic behavior.
Journal of Fixed Point Theory and Applications,
Vol. 27,
Issue. 1,
Wang, Guotao
and
Guo, Mengjie
2025.
The multiplicity of radial p-k-convex solutions for the p-k-Hessian equation.
Journal of Applied Mathematics and Computing,
Vol. 71,
Issue. 1,
p.
927.
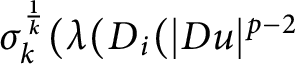 $\sigma _{k}^{\frac 1k} ( \lambda ( D_{i} (|Du|^{p-2}$
$\sigma _{k}^{\frac 1k} ( \lambda ( D_{i} (|Du|^{p-2}$
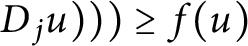 $ D_{j}u ) ) ) \geq f(u)$
on the entire space
$ D_{j}u ) ) ) \geq f(u)$
on the entire space
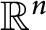 $\mathbb {R}^{n}$
and provide a necessary and sufficient condition, which can be regarded as a generalized Keller–Osserman condition. Furthermore, we obtain the optimal regularity of solution.
$\mathbb {R}^{n}$
and provide a necessary and sufficient condition, which can be regarded as a generalized Keller–Osserman condition. Furthermore, we obtain the optimal regularity of solution.