Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T17:38:01.413Z Has data issue: false hasContentIssue false
  • English
  • Français

Limiting Properties of the Distribution of Primes in an Arbitrarily Large Number of Residue Classes

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Set functions and measures on spaces with additional structure Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  30 January 2020

Lucile Devin
Lucile Devin*
Affiliation:
Centre de recherches mathématiques, Université de Montréal, Pavillon André-Aisenstadt, 2920 Chemin de la tour, Montréal, Québec, H3T 1J4Canada Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize current known distribution results on Shanks–Rényi prime number races to the case where arbitrarily many residue classes are involved. Our method handles both the classical case that goes back to Chebyshev and function field analogues developed in the recent years. More precisely, let 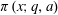$\unicode[STIX]{x1D70B}(x;q,a)$ be the number of primes up to $x$ that are congruent to $a$ modulo 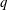$q$. For a fixed integer 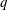$q$ and distinct invertible congruence classes $a_{0},a_{1},\ldots ,a_{D}$, assuming the generalized Riemann Hypothesis and a weak version of the linear independence hypothesis, we show that the set of real $x$ for which the inequalities 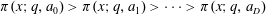$\unicode[STIX]{x1D70B}(x;q,a_{0})>\unicode[STIX]{x1D70B}(x;q,a_{1})>\cdots >\unicode[STIX]{x1D70B}(x;q,a_{D})$ are simultaneously satisfied admits a logarithmic density.

Keywords

Chebyshev’s biasalmost-periodic functionregularity of measure

MSC classification

Primary: 11K70: Harmonic analysis and almost periodicity
Secondary: 28C15: Set functions and measures on topological spaces (regularity of measures, etc.) 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 837 - 849
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by a Postdoctoral Fellowship at the University of Ottawa.

References

Akbary, A., Ng, N., and Shahabi, M., Limiting distributions of the classical error terms of prime number theory. Q. J. Math. 65(2014), no. 3, 743–780. https://doi.org/10.1093/qmath/hat059CrossRefGoogle Scholar
Cha, B., Chebyshev’s bias in function fields. Compos. Math. 144(2008), no. 6, 1351–1374. https://doi.org/10.1112/S0010437X08003631CrossRefGoogle Scholar
Cha, B., Fiorilli, D., and Jouve, F., Prime number races for elliptic curves over function fields. Ann. Sci. Éc. Norm. Supér. (4) 49(2016), no. 5, 1239–1277. https://doi.org/10.24033/asens.2308CrossRefGoogle Scholar
Cha, B., Fiorilli, D., and Jouve, F., Independence of the zeros of elliptic curve L-functions over function fields. Int. Math. Res. Not. IMRN 2017(2017), no. 9, 2614–2661. https://doi.org/10.1093/imrn/rnw087Google Scholar
Cha, B. and Im, B.-H., Chebyshev’s bias in Galois extensions of global function fields. J. Number Theory 131(2011), no. 10, 1875–1886. https://doi.org/10.1016/j.jnt.2011.03.011CrossRefGoogle Scholar
Cha, B. and Kim, S., Biases in the prime number race of function fields. J. Number Theory 130(2010), no. 4, 1048–1055. https://doi.org/10.1016/j.jnt.2009.09.015CrossRefGoogle Scholar
Chebyshev, P. L., Oeuvres. Tome I, ch. Lettre de M. le professeur Tchebychev à M. Fuss, sur le nouveau théorème relatif aux nombres premiers contenus dans les formes 4n + 1 et 4n + 3, Commissionaires de l’Academie imperiale des sciences, St. Petersbourg, 1899, pp. 697–698.Google Scholar
Devin, L., Chebyshev’s bias for analytic L-functions. Mathematical Proceedings of the Cambridge Philosophical Society, 2019, pp. 1–38.Google Scholar
Devin, L. and Meng, X., Chebyshev’s bias for products of irreducible polynomials. Preprint, 2018. arxiv:1809.09662.Google Scholar
Ford, K. and Konyagin, S., Chebyshev’s conjecture and the prime number race. In: IV international conference “modern problems of number theory and its applications”: current problems, Part II (Russian) (Tula, 2001). Mosk. Gos. Univ. im. Lomonosova, Mekh.-Mat. Fak., Moscow, 2002, pp. 67–91.Google Scholar
Granville, A. and Martin, G., Prime number races. Amer. Math. Monthly 113(2006), no. 1, 1–33. https://doi.org/10.2307/27641834CrossRefGoogle Scholar
Humphries, P., The Mertens and Pólya conjectures in function fields. Master’s thesis, 2012. http://hdl.handle.net/1885/148266.Google Scholar
Kowalski, E., The large sieve, monodromy, and zeta functions of algebraic curves. II. Independence of the zeros. Int. Math. Res. Not. IMRN 2008(2008), Art. ID rnn 091.Google Scholar
Kaczorowski, J. and Ramaré, O., Almost periodicity of some error terms in prime number theory. Acta Arith. 106(2003), no. 3, 277–297. https://doi.org/10.4064/aa106-3-6CrossRefGoogle Scholar
Keating, J. P. and Rudnick, Z., The variance of the number of prime polynomials in short intervals and in residue classes. Int. Math. Res. Not. IMRN 2014(2014), no. 1, 259–288. https://doi.org/10.1093/imrn/rns220CrossRefGoogle Scholar
Lang, S., Algebra, Third ed., Graduate Texts in Mathematics, Vol. 211, Springer-Verlag, New York, 2002. https://doi.org/10.1007/978-1-4613-0041-0CrossRefGoogle Scholar
Li, W., Vanishing of hyperelliptic L-functions at the central point. J. Number Theory 191(2018), 85–103. https://doi.org/10.1016/j.jnt.2018.03.018CrossRefGoogle Scholar
Lichtman, J. D., Martin, G., and Pomerance, C., Primes in prime number races. Proc. Amer. Math. Soc. 147(2019), no. 9, 3743–3757. https://doi.org/10.1090/proc/14569CrossRefGoogle Scholar
Martin, G. and Ng, N., Inclusive prime number races. Trans. Amer. Math. Soc. 373(2020), no. 5, 3561–3607. https://doi.org/10.1090/tran/7996CrossRefGoogle Scholar
Perret-Gentil, C., Roots of L-functions of characters over function fields and of Kloosterman sums: generic linear independence and consequences. Algebra and Number Theory, to appear.Google Scholar
Rosen, M., Number theory in function fields. Graduate Texts in Mathematics, Vol. 210, Springer-Verlag, New York, 2002. https://doi.org/10.1007/978-1-4757-6046-0CrossRefGoogle Scholar
Rubinstein, M. and Sarnak, P., Chebyshev’s bias. Experiment. Math. 3(1994), no. 3, 173–197.10.1080/10586458.1994.10504289CrossRefGoogle Scholar
Rudnick, Z. and Waxman, E., Angles of Gaussian primes. Israel J. Math. 232(2019), 159–199. https://doi.org/10.1007/s11856-019-1867-5CrossRefGoogle Scholar
Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, Vol. 43, Princeton University Press, Princeton, NJ, 1993.Google Scholar
Weil, A., Sur les courbes algébriques et les variétés qui s’en déduisent. Actualités Sci. Ind. 1041. Publ. Inst. Math. Univ. Strasbourg 7(1945), Hermann et Cie., Paris, 1948.Google Scholar