No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
For 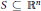 $S\,\subseteq \,{{\mathbb{R}}^{n}}$ a set
$S\,\subseteq \,{{\mathbb{R}}^{n}}$ a set 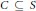 $C\,\subseteq \,S$ is an
$C\,\subseteq \,S$ is an  $m$-clique if the convex hull of no
$m$-clique if the convex hull of no  $m$-element subset of
$m$-element subset of  $C$ is contained in
$C$ is contained in  $S$. We show that there is essentially just one way to construct a closed set
$S$. We show that there is essentially just one way to construct a closed set 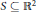 $S\,\subseteq \,{{\mathbb{R}}^{2}}$ without an uncountable 3-clique that is not the union of countably many convex sets. In particular, all such sets have the same convexity number; that is, they require the same number of convex subsets to cover them. The main result follows from an analysis of the convex structure of closed sets in
$S\,\subseteq \,{{\mathbb{R}}^{2}}$ without an uncountable 3-clique that is not the union of countably many convex sets. In particular, all such sets have the same convexity number; that is, they require the same number of convex subsets to cover them. The main result follows from an analysis of the convex structure of closed sets in  ${{\mathbb{R}}^{2}}$ without uncountable 3-cliques in terms of clopen,
${{\mathbb{R}}^{2}}$ without uncountable 3-cliques in terms of clopen, 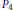 ${{P}_{4}}$-free graphs on Polish spaces.
${{P}_{4}}$-free graphs on Polish spaces.