This paper features strong and weak compactness in spaces of vector measures with relatively compact ranges in Banach spaces. Its tools are the measure-operator identification of [16] and [24] and the description of strong and weak compactness in spaces of compact operators in [10], [11], and [29].

Given a Banach space X and an algebra of sets, it is shown in [16] that under the usual identification via integration of X-valued bounded additive measures on with X-valued sup norm continuous linear operators on the space of -simple scalar functions, the strongly bounded, countably additive measures correspond exactly to those operators which are continuous for the coarser (locally convex) universal measure topology τ on . It is through the latter identification that the results on strong and weak compactness in [10], [11], and [29] can be applied to X-valued continuous linear operators on the generalized DF space to yield results on strong and weak compactness in spaces of vector measures.

Let X be a topological space and let A ⊂ X. The character of A in X is the minimal cardinal of a base for the neighborhoods of A in X. Previous studies have shown that the character of certain subsets of X (or of X2) is related to compactness conditions on X. For example, in [12], Ginsburg proved that if the diagonal

of a space X has countable character in X2, then X is metrizable and the set of nonisolated points of X is compact. In [2], Aull showed that if every closed subset of X has countable character, then the set of nonisolated points of X is countably compact. In [18], we noted that if every closed subset of X has countable character, then MA + ┐ CH (Martin's axiom with the negation of the continuum hypothesis) implies that X is paracompact.

In [18], the author initiated an investigation of compact, Banach-module-valued derivations of C*-algebras. In collaboration with C. A. Akemann [3] and S.-K. Tsui [16], he determined the structure of all compact and weakly compact, A-valued derivations of a C*-algebra A, and of all compact, B(H)-valued derivations of a C*-subalgebra of B(H), the algebra of bounded linear operators on a Hilbert space H. In this paper, we begin the study of weakly compact, B(H)-valued derivations of C*-subalgebras of B(H).

Let R be a C*-subalgebra of B(H), δ:R → B(H) a weakly compact derivation, i.e., a weakly compact linear map which has

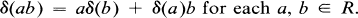
Since δ has a unique weakly compact extension to a derivation of the closure of R in the weak operator topology (WOT) on B(H) (consult the proof of Theorem 3.1 of [16]), we may assume with no loss of generality that R is a von Neumann subalgebra of B(H). In this paper, we determine in Lemma 4.1 and Theorems 4.3 and 4.10 the structure of δ when R is type I, using I. E. Segal's multiplicity theory [14] for type I von Neumann algebras and results of E. Christensen [6], [7] on B(H)-valued derivations of von Neumann algebras.

We consider polynomials of the form

with non-zero coefficients ai in a finite field F. For any finite extension field K ⊇ F, let fk:Kn → K be the mapping defined by f. We say f is universal over K if fK is surjective, and f is isotropic over K if fK has a non-trivial “kernel“; the latter means fK(X) = 0 for some 0 ≠ x ∊ Kn.

We show (Theorem 1) that f is universal over K provided |K| (the cardinality of K) is larger than a certain explicit bound given in terms of the exponents d1,…, dn. The analogous fact for isotropy is Theorem 2.

It should be noted that in studying diagonal equations

we fix both the number of variables n and the exponents di, and ask how large the field must be to guarantee a solution.

We say that two elements e and f of a lattice are moderately separated provided e ∧ f = 0 and both (e′, f′) and (f′, e′) are modular pairs for all e′ ≦ e and f′ ≦ f. Here (e′, f′) a modular pair means that, for all g ≧ e′,

In the lattice of projections of a factor we show that e and f, with e ∧ f = 0, are modularly separated if and only if ‖(e – k)f‖ < 1 for some finite projection k ≦ e. From there we can show that a kind of “independence property” holds for modular separation in this case: if e and f are modularly separated and if e ∨ f and g are modularly separated, then e and f ∧ g are modularly separated.

By classical results of Ambrust and Schmidt, every monoid is isomorphic to the endomorphism monoid of an algebra. Thus if we want to investigate in which varieties (or generally, in a concrete category) each monoid is isomorphic to the endomorphism monoid of an algebra in this variety (or an object of this category) then the important role is played by the concept of a binding category (see the definition below). Moreover, as shows the Hedrlín-Kučera Theorem [13] if the set-theoretical assumption (M) holds (i.e., there is an infinite cardinal α such that each ultrafilter closed under α intersections is trivial) every concrete category can be fully embedded into any binding category. Other properties of binding categories are in [7, 11, 13]. A list of the most important binding categories and the properties of binding categories can be found in an excellent monograph [13].

By a projectivityof vector spaces Xand Yover fields F and G is meant an isomorphism Ψ:(X) → (Y) of their lattices of subspaces. A basic theorem of projective geomtry [2, p. 44] asserts that, for spaces of dimension at least 3, any such projectivity is of the form Ψ(M) = SM for a bijection S:X → Y which is semi-linear in the sense that S is an additive mapping for which there exists an isomorphism σ:F→ G such that

S(λx) = σ(λ)Sx for all λ ∈ Fand all x∈ X.

In [12] Mackey obtained a continuous version of this result: for real normed linear spaces Xand Y, the lattices and of closed subspaces are isomorphic if and only if X and Yare isomorphic (i.e., via a bicontinuous linear bijection).

Let X be a Riemann surface, and H∞(X) the ring of bounded holomorphic functions in X. We offer here a question on divisibility in H∞(X), and then give in Section 2 a condition in which the answer is yes (Corollary 2 to Lemma 1). In Section 3 we use part 2 to prove a theorem on the separation of points by H∞(X). In Section 4 we study X/H∞(X).

If f is meromorphic in X and z ∈ X, then by o(f, z) we mean the order of f at z. (We agree that o(f, z) = ∞ if f ≡ 0.) Let h be memomorphic in X; then h might be said to be of bounded type if h = f/g where f,g ∈ H∞(X), g ≠ 0.

Cauchy spaces were introduced by Kowalsky in 1954 [9]. In that paper a first completion method for these spaces was given. In 1968 Keller [5] has shown that the Cauchy space axioms characterize the collections of Cauchy filters of uniform convergence spaces in the sense of [1]. Moreover in the completion theory of uniform convergence spaces the associated Cauchy structures play an essential role [12]. This fact explains why in the past ten years in the theory of Cauchy spaces, much attention has been given to the study of completions.

The measure (x1x2x3)2adm(x) on the unit sphere in R3 is invariant under sign-changes and permutations of the coordinates; here dm denotes the rotation-invariant surface measure. The more general measure

corresponds to the measure

on the triangle

(where ). Appell ([1] Chap. VI) constructed a basis of polynomials of degree n in v1, v2 orthogonal to all polynomials of lower degree, and a biorthogonal set for the case γ = 0. Later Fackerell and Littler [6] found a biorthogonal set for Appell's polynomials for γ ≠ 0. Meanwhile Pronol [10] had constructed an orthogonal basis in terms of Jacobi polynomials.

E. Salow [8] introduced the concept of pre-Hjelmslev groups, a generalization of F. Bachmann's Hjelmslev groups [1] which leads to a more natural theory of homomorphisms and permits a simpler construction of algebraic models. Basically, both types of groups are the groups of motions of a metric plane, the so-called group plane. In such a plane there is a unique perpendicular through any point to any line and the product of three collinear points (three copunctal lines) is a point (a line). Our first section contains the precise definitions and some basic facts.

The homomorphic image of a pre-Hjelmslev group can be more complicated than the pre-image. For instance, there may always be a unique line through two distinct points of the pre-image but not of the image. We study regular homomorphisms of pre-Hjelmslev groups, i.e., homomorphisms with the following property: If two lines intersect at exactly one point, their images will also have precisely one point in common.

Let x = (x1, … xn) denote a point of Euclidean n space En and set Di = ∂/∂xi for i = 1, … n. Let Ω denote an exterior domain in En with smooth boundary and consider in Ω the formal elliptic problem:

1

We first consider the problem of finding nonnegative generalized solutions of (1) when τ ≧ 0, τ ≢ 0, and r(x) ≡ 0. Under more stringent conditions on the coefficients and for suitable r(x), we then show the existence of a locally bounded solution. Next, we show that, under stronger assumptions, our main criterion is also necessary. The final arguments are devoted to the consideration of illustrative examples.

In many basic linear algebra texts it is shown that various classes of square matrices (normal, positive, invertible) possess square roots. In this note we characterize those n × n matrices with complex entries which possess at least one square root without any restriction on the class of root or matrix involved. We then use this characterization to obtain asymptotic estimates for the relative profusion of such matrices.

In Section 1 we characterize those n × n matrices with entries in C (or any algebraically complete field) which have square roots over C. This characterization is in terms of similarity classes. In Section 2 we give asymptotic estimates for the number of Jordan forms of nilpotent n × n matrices which are squares. Section 3 is given over to numerical results concerning the actual and asymptotic frequency of such forms.

Let M and N be connected Hermitian manifolds of dimensions m and n with Hermitian metrics hM and hN, respectively. Then the space ℓ(M, N) of continuous mappings between M and N endowed with the compact-open topology is second countable so that a metric can be furnished in ℓ(M, N) which induces the compact-open topology. A sequence {fn} in ℓ(M, N) converges to a n f in ℓ(M, N) in this topology if and only if fn converges to f uniformly on compact subsets of M. It is then an easy consequence of the Cauchy integral formula to show that the space ℋ(M, N) of holomorphic mappings f:M → N is a closed subspace of ℓ(M, N).

In this paper, generalizing the classical notions of normal functions, Bloch functions, regular sequences and P-point sequences of one complex variable to the mappings in ℋ(M, N), see also [25], we obtain various relations which exist between these notions.

Soit M un facteur de type IIIλ 0 ≦ λ< 1, agissant sur un espace hilbertien à base dénombrable. Le propos de ce travail est l'étude des états normaux d'un tel facteur à équivalence unitaire près. L'espace quotient n'est pas séparé; l'espace séparé associé est obtenu comme quotient de l'espace des états normaux par la relation d'équivalence R dont les classes sont les fermetures des orbites précédentes.

Pour étudier cet espace, on définit un calcul fonctionnel sur M+* (espace des formes linéaires positives normales sur M) à valeurs dans M. Ce calcul fonctionnel est déterminé par la donnée d'une C* algèbre d'applications de M+ * dans M “continues” en un certain sens, notée C*(M).

The following well known inequality was first proved by Bernstein [2].

THEOREM A. If pn(x) is a polynomial of degree n, such that |pn(x)| ≦ 1 for –1 ≦ x = +1, then

1

The dominant n(1 – x2)–;1/2 is best possible only at the zeros of the Tchebychev polynomial

but the bound is precise at every interior point as far as the exponent of n is concerned.

Theorem A was extended to the case of higher derivatives by Duffin and Schaeffer in [4]. In that paper they make extensive use of the oscillation property of the polynomial Tn(x) and of the related function

J. M. Borwein has given in [1] a practical necessary and sufficient condition for a convex operator to be continuous at some point. Indeed J. M. Borwein has proved in his paper that a convex operator with values in an order topological vector space F (with normal positive cone F+) is continuous at some point if and only if it is bounded from above by a mapping which is continuous at this point. This result extends a previous one by M. Valadier in [16] asserting that a convex operator is continuous at a point whenever it is bounded from above by an element in F on a neighbourhood of the concerned point. Note that Valadier's result is necessary if and only if the topological interior of F+ is nonempty. Obviously both results above are generalizations of the classical one about real-valued convex functions formulated in this context exactly as Valadier's result (see for example [5]).

In this paper we are concerned with the space BMOA of analytic functions of bounded mean oscillation for Riemann surfaces, and it is shown that for any analytic function on a Riemann surface the area of its range set bounds the square of its BMO norm, from which it is seen as an immediate corollary that the space BMOA includes the space AD of analytic functions with finite Dirichlet integrals.

Let R be an open Riemann surface which possesses a Green's function, i.e., R ∉ OG, and f b e an analytic function defined on R. The Dirichletintegral DR(f) = D(f) of f on R is defined by

1.1

and we denote by AD(R) the space of all functions f analytic on R for which D(f) < +∞.

In the literature about the definition of data types there exist many approaches using some concept of fixed point. Wand [13] and Lehmann, Smyth [9] e.g. constructed data types as least fixed points of functors F:K → K. Arbib and Manes [3] showed that some data types turn out to be the greatest fixed points of such endofunctors. In this paper we regard least and greatest fixed points that have a given property.

In a recent paper [12], C. Mueller proved a general version of the functional LIL which unifies Strassen's LIL and the Lévy modulus of continuity for Brownian motion W(t). His theorem also contains other known forms of the LIL.

For each t ≧ 0, let be a family of points in the first quadrant of the plane. Let r ≦ 0; to each point (s0, l0), we associate a rectangle

Define Ar(t) to be the area of the union of these rectangles up to time t under the measure . Then, Theorem 1 [12, p. 166] states that for an increasing function h such that

the set of limit points of

in C[0, 1] is the closed unit ball of the reproducing kernel Hilbert space (rkhs) associated with Wiener measure.