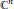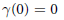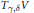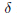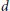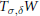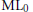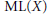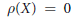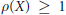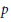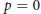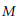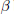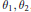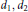Research Article
Convex Bodies of Minimal Volume, Surface Area and Mean Width with Respect to Thin Shells
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-32
-
- Article
-
- You have access
- Export citation
Higher Order Tangents to Analytic Varieties along Curves. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-63
-
- Article
-
- You have access
- Export citation
Classification of Linear Weighted Graphs up to Blowing-Up and Blowing-Down
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-87
-
- Article
-
- You have access
- Export citation
Nilpotent Conjugacy Classes in
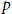 $p$-adic Lie Algebras: The Odd Orthogonal Case
$p$-adic Lie Algebras: The Odd Orthogonal Case
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 88-108
-
- Article
-
- You have access
- Export citation
Affine Lines on Affine Surfaces and the Makar–Limanov Invariant
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-139
-
- Article
-
- You have access
- Export citation
On the Geometry of
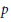 $p$-Typical Covers in Characteristic
$p$-Typical Covers in Characteristic 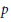 $p$
$p$
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-163
-
- Article
-
- You have access
- Export citation
Boundary Structure of Hyperbolic 3-Manifolds Admitting Annular and Toroidal Fillings at Large Distance
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 164-188
-
- Article
-
- You have access
- Export citation
Furstenberg Transformations and Approximate Conjugacy
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 189-207
-
- Article
-
- You have access
- Export citation
Constructing Galois Representations with Very Large Image
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 208-221
-
- Article
-
- You have access
- Export citation
Amibes de sommes d’exponentielles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-240
-
- Article
-
- You have access
- Export citation