Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T23:04:57.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Convex Bodies of Minimal Volume, Surface Area and Mean Width with Respect to Thin Shells

Published online by Cambridge University Press:  20 November 2018

Károly Böröczky ,
Károly J. Böröczky ,
Carsten Schütt  and
Gergely Wintsche
Károly Böröczky
Affiliation:
Department of Geometry, Roland Eötvös University, Budapest, Pázmány Péter sétány 1/C, H-1117, Hungary e-mail: [email protected]
Károly J. Böröczky
Affiliation:
Alfréd Rényi Institute of Mathematics, PO Box 127, H-1364, Budapest Hungary e-mail: [email protected]
Carsten Schütt
Affiliation:
Mathematisches Seminar, Christian Albrechts Universität, 24098 Kiel, Germany e-mail: [email protected]
Gergely Wintsche
Affiliation:
Teacher Training Department, Roland Eötvös University, Pázmány Péter sétány 1/C, H-1117, Budapest, Hungary e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given 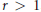$r\,>\,1$, we consider convex bodies in 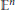${{\mathbb{E}}^{n}}$ which contain a fixed unit ball, and whose extreme points are of distance at least 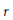$r$ from the centre of the unit ball, and we investigate how well these convex bodies approximate the unit ball in terms of volume, surface area and mean width. As 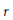$r$ tends to one, we prove asymptotic formulae for the error of the approximation, and provide good estimates on the involved constants depending on the dimension.

Keywords

Primary52A27secondary52A40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 3 - 32
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Artin, E., The Gamma Function. Holt, Rinehart and Winston, New York, 1964.Google Scholar
[2] Mathéné Bognár, K. and Böröczky, K., Regular polyhedra and Hajós polyhedra. Studia Sci. Math. Hungar. 35(1999), no. 3-4, 415–426.Google Scholar
[3] Böröczky, K. and Böröczky, K., Jr. Polytopes of minimal volume with respect to a shell - another characterization of the octahedron and the icosahedron. Disc. Comput. Geom., to appear. http://www.renyi.hu/˜carlos/radiusmain.pdf Google Scholar
[4] Böröczky, K., Böröczky, K., Jr., and Wintsche, G., Typical faces of extremal polytopes with respect to a thin three-dimensional shell. Periodica Math Hung. 53(2006), no. 1-2, 83–102.Google Scholar
[5] Böröczky, K., Jr. and Reitzner, M., Approximation of smooth convex bodies by random circumscribed polytopes. Ann. Appl. Prob. 14(2004), 239–273.Google Scholar
[6] Böröczky, K. J., Tick, P., and Wintsche, G., Typical faces of best approximating three-polytopes, preprint. http://www.renyi.hu/˜carlos/approxface.pdf Google Scholar
[7] Böröczky, K., Jr. and Wintsche, G.: Covering the sphere by equal spherical balls. In: Discrete and Computational Geometry. Algorithms Combin. 25, Springer, Berlin, 2003, 237–253.Google Scholar
[8] Falconer, K. J., The Geometry of Fractal Sets. Cambridge Tracts in Mathematics 85, Cambridge University Press, Cambridge, 1985.Google Scholar
[9] Tóth, L. Fejes, Regular Figures. Pergamon Press, New York, 1964.Google Scholar
[10] Giannopoulos, A. A. and Milman, V. D., Asymptotic convex geometry: short overview. In: Different Faces of Geometry. Int. Math. Ser. (N.Y.) 3, Kluwer/Plenum, New York, 2004, pp. 87–162.Google Scholar
[11] Gruber, P. M., Aspects of approximation of convex bodies. In: Handbook of Convex Geometry. North-Holland, Amsterdam, 1993, pp. 319–345.Google Scholar
[12] Gruber, P. M., Comparisons of best and random approximation of convex bodies by polytopes. Rend. Circ. Mat. Palermo, 50(1997), 189–216.Google Scholar
[13] Gruber, P. M., Optimale Quantisierung. Math. Semesterber. 49(2002), no. 2, 227–251.Google Scholar
[14] Gruber, P. M., Optimum quantization and its applications. Adv. Math. 186(2004), no. 2, 456–497.Google Scholar
[15] Molnár, J., Alcune generalizzazioni del teorema di Segre-Mahler. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. 30(1961), 700–705.Google Scholar
[16] Rogers, C. A., Hausdorff Measure. Cambridge University Press, London, 1970.Google Scholar
[17] Sangwine-Yager, J. R., A generalization of outer parallel sets of a convex set. Proc. Amer.Math. Soc. 123(1995), no. 5, 1559–1564.Google Scholar
[18] Schneider, R., Zur optimalen Approximation konvexer Hyperflächen durch Polyeder. Math. Ann. 256(1981), no. 3, 289–301.Google Scholar
[19] Schneider, R.. Convex Bodies: the Brunn-Minkowski theory. Encyclopedia of Mathematics and its Applications 44, Cambridge Univ. Press, 1993.Google Scholar