Research Article
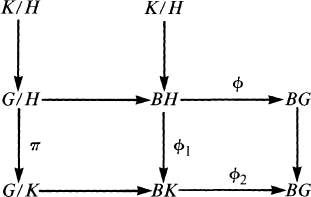
Maximal Homotopy Lie Subgroups of Maximal Rank
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 769-787
-
- Article
-
- You have access
- Export citation
On Divisors of Sums of Integers IV
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 788-816
-
- Article
-
- You have access
- Export citation
Notions De Base Pour L'Arthmetique De Fq((1/t))
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 817-832
-
- Article
-
- You have access
- Export citation
Strong Morita Equivalence for Heisenberg C*-Algebras and the Positive Cones of Their K0-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 833-864
-
- Article
-
- You have access
- Export citation
Semicontinuity and Multipliers of C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 865-988
-
- Article
-
- You have access
- Export citation
On the Hankel and Some Related Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 989-1009
-
- Article
-
- You have access
- Export citation
Representation Formulas for Integrable and Entire Functions of Exponential Type I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1010-1024
-
- Article
-
- You have access
- Export citation

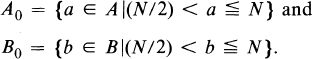
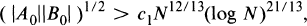
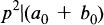
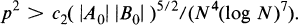
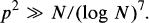
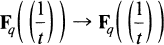
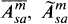 , and
, and 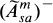 (notation explained in Section 2), and we will call these the classes of
(notation explained in Section 2), and we will call these the classes of 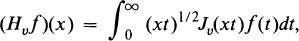
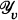 and
and 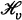 transformations defined for such
transformations defined for such 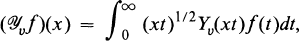
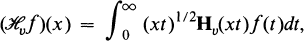
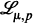 defined in [
defined in [
 is the so called conjugate function of
is the so called conjugate function of 