Article contents
Maximal Homotopy Lie Subgroups of Maximal Rank
Published online by Cambridge University Press: 20 November 2018
Extract
Let G be a compact connected Lie group with H a connected subgroup of maximal rank. Suppose there exists a compact connected Lie subgroup K with H ⊂ K ⊂ G. Then there exists a smooth fiber bundle G/H → G/K with K/H as the fiber. (See for example [13].) This can be incorporated into a diagram involving the classifying spaces as follows:
(1)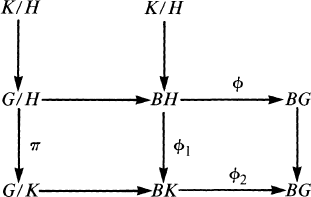
Here π, ϕ, ϕ1 and ϕ2 denote fibrations. We also know that the homogeneous spaces and the Lie groups, which are homotopy equivalent to the loop spaces of their respective classifying spaces, are homotopy equivalent to connected finite complexes.
Now suppose H is a maximal subgroup. Can there still exist spaces, which we will call BK, K/H, and G/K, and fibrations so that diagram (1) is still valid? This paper will show that in many cases either G/K or K/H will be homo topically trivial.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
- 1
- Cited by


