Research Article
On the Galois Theory of Commutative Rings II: Automorphisms induced in Residue Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1025-1037
-
- Article
-
- You have access
- Export citation
A Lower Bound for the Volume of Hyperbolic 3-Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1056
-
- Article
-
- You have access
- Export citation
Univalent and Starlike Generalized Hypergeometric Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1057-1077
-
- Article
-
- You have access
- Export citation
Dual Space Derivations and H2(L, F) of Modular Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1078-1106
-
- Article
-
- You have access
- Export citation
On the Sieve of Eratosthenes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1107-1122
-
- Article
-
- You have access
- Export citation
Uniformly Closed Algebras Generated by Boolean Algebras of Projections in Locally Convex Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1123-1146
-
- Article
-
- You have access
- Export citation
Théorèmes de Convergence Locale Pour Les Résolvantes et Les Processus Abéliens à Plusieurs Paramètres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1147-1161
-
- Article
-
- You have access
- Export citation
Semilinear Elliptic Problems with Pairs of Decaying Positive Solutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1162-1173
-
- Article
-
- You have access
- Export citation
The Multiple Q-Construction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1174-1209
-
- Article
-
- You have access
- Export citation
THE C1-Invariance of the Godbillon-Vey Map in Analytical K-Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1210-1222
-
- Article
-
- You have access
- Export citation
Idempotent Multipliers of H1(T)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1223-1234
-
- Article
-
- You have access
- Export citation
Commutator Theory on Hilbert Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1235-1280
-
- Article
-
- You have access
- Export citation

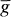 in the residue ring
in the residue ring 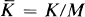 , and if
, and if 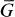 is the group consisting of all
is the group consisting of all 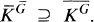
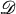 if it never takes on the same value twice, that is, if
if it never takes on the same value twice, that is, if 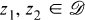 implies that
implies that 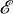 is said to be starlike with respect to
is said to be starlike with respect to 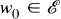 the line segment joining
the line segment joining 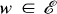 lies entirely in
lies entirely in  , the number of natural numbers not exceeding
, the number of natural numbers not exceeding 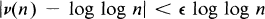
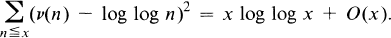


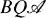 of the
of the 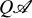 of an exact category
of an exact category 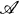 , which would be understandable to the man on the street, and which also would be well-behaved with respect to products induced by biexact pairings. Gillet [
, which would be understandable to the man on the street, and which also would be well-behaved with respect to products induced by biexact pairings. Gillet [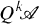 . Shimakawa [
. Shimakawa [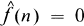 for all integers
for all integers 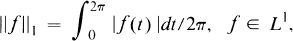
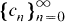 in
in