Denote by C0 the collection of complex-valued functions which are continuous and compactly supported on (0, ∞). The transformations of the title are defined on C0 by

1.1

and

1.2

respectively, where Yv(x) is the Bessel function of the second kind, and Hv(x) is the Struve function; see [1; 7.5.4(55)]. The two transformations are studied briefly in [6; §8.4]; tables of transform pairs are given in [2; Chapters IX and XI], where it is also stated that, for – , each of the transformations is the inverse of the other.

Throughout this paper we shall use I to denote a given interval, not necessarily bounded, of real numbers and Cn to denote the real valued n times continuously differentiable functions on I and C0 will be abbreviated to C. By a differential operator of order n we shall mean a linear function L:Cn → C of the form

1.1

where pn(x) ≠ 0 for x ∊ I and pi ∊ Cj 0 ≦ j ≦ n. The function pn is called the leading coefficient of L.

It is well known (see, for example, [2, pp. 73-74]) thai a differential operator L of order n uniquely determines both a differential operator L* of order n (the adjoint of L) and a bilinear form [·,·]L (the Lagrange bracket) so that if D denotes differentiation, we have for u, v ∊ Cn,

1.2

The purpose of this paper is to show how Fred hoi m criteria for Toeplitz operators, whose symbols lie in an algebra,A, may often be generalized to cover a larger symbol algebra generated by A and SO, the slowly oscillating functions. Mere A and SO are algebras of continuous functions on the real line, so that we are concerned principally with the effect of a single discontinuity in the symbol function.

We shall treat the cases when A is the almost periodic functions, the semi-almost periodic functions and the multiplicatively periodic functions. Sufficient criteria for Fredholmness are obtained in Section 5. The more difficult task of establishing necessary and sufficient criteria is only achieved here for the slowly oscillating almost periodic functions and this is done in Section 6.

A space is H(i) [R(i)] if every open [regular] filter base has a cluster point and H(ii) [R(ii)] if every open [regular] filter base with a unique cluster point converges. This terminology is due to C. T. Scarborough and A. H. Stone [11]; H(i) spaces have been studied as quasi-H-closed spaces in [10] and as generalized absolutely closed spaces in [6]. Hausdorff H(i) [H(ii)] spaces are called H-closed [minimal Hausdorff] and regular T1 R(i) [R(ii)] spaces are called R-closed [minimal regular]. For a space X, 2X is the set of all non-empty closed subsets of X with the finite topology [8]. The present study was motivated by the longstanding problem of whether or not a T3 space with every closed subset R-closed is compact, and also by the well-known result ([8] and [14]) that X is compact if and only if 2X is compact.

In [4] and [5], R. C. James introduced a non-reflexive Banach space J which is isometric to its second dual. Developing new techniques in the theory of Schauder bases, James identified J**, showed that the canonical image of J in J** is of codimension one, and proved that J** is isometric to J.

In Section 2 of this paper we show that J, equipped with an equivalent norm, is a semi-simple (commutative) Banach algebra under point wise multiplication, and we determine its closed ideals. We use the Arens multiplication and the Gelfand transform to identify J**, which is in fact just the algebra obtained from J by adjoining an identity.

How many of the continuous maps of a simple closed curve to itself are slope-preserving? For the unit circle S1 with centre (0, 0), a continuous map σ of S1 to S1 is slope-preserving if and only if σ is the identity map [σ(x, y) = (x, y)] or σ is the antipodal map [σ(x, y) = (–x, –y)]. Besides the identity map, more general simple closed curves can also possess an “antipodal” map (cf. Figure 1).

A translation plane of dimension d over its kernel K = GF(q) can be represented by a vector space of dimension 2d over K. The lines through the zero vector form a “spread”; i.e., a class of mutually independent vector spaces of dimension d which cover the vector space.

The case where d = 2 has aroused the most interest. The more exotic translation planes tend to be of dimension two; a spread in this case can be interpreted as a class of mutually skew lines in projective three-space.

The stabilizer of the zero vector in the group of collineations is a group of semi-linear transformations and is called the translation complement. The subgroup consisting of linear transformations is the linear translation complement.

An n2 × k orthogonal array is a pair (P, B) where P = {1, 2, …, n} and B is a collection of k-tuples of elements from P (called rows) such that if i < j ∈ {1, 2, …, k} and x and y are any two elements of P (not necessarily distinct) there is exactly one row in B whose ith coordinate is x and whose jth coordinate is y. We will refer to the ith coordinate of a row r as the ith column of r. The number n is called the order (or size) of the array and k is called the strength.

In his thesis and [24], J. B. Nation showed the existence of certain lattice identities, strictly weaker than the modular law, such that if all the congruence lattices of a variety of algebras satisfy one of these identities, then all the congruence lattices were even modular. Moreover Freese and Jónsson showed in [10] that from this “congruence modularity” of a variety of algebras one can even deduce the (stronger) Arguesian identity.

These and similar results [3; 5; 9; 12; 18; 21] induced Jónsson in [17; 18] to introduce the following notions. For a variety of algebras , is the (congruence) variety of lattices generated by the class () of all congruence lattices θ(A), . Secondly if is a lattice identity, and Σ is a set of such, holds if for any variety implies .

In recent years there has been considerable interest in the conjecture that |G| divides |Aut G| for all finite non-cyclic p-groups G of order greater than p2. In particular, the conjecture has been established for a considerable number of (not necessarily distinct) classes of finite p-groups ([6], [7], [8], [9], [15], [16]); additionally, results have been obtained, often using homological methods, which permit reductions in any attempt to establish the overall conjecture ([5], [10], [13], [15]). In the former case, the p-groups G have generally been regular p-groups (see, for example, [6]) and the prime p = 2 has either been excluded (see, for example, [8]) or treated as a special case (as in [9]).It is the purpose of this paper to establish the conjecture for the class of all p-groups G where |G: Z(G)| ≦ p4 with no restrictions on the prime p.

The proof of a main result in [1] concerning (0,1)-endomorphisms of finite lattices is based on properties of lattices A(G) derived from the system of independent sets of an undirected loop-free graph G. For a number of questions naturally arising from [1] and [2], however, constructions employing only graph-induced complementation and properties of the lattices A (G) associated with these are no longer adequate. The present paper introduces cover set lattices (a generalization of the lattices A(G)) to deal with some of these questions. A special case of the main result presented here states that for every (0, 1)-lattice L and any monoid homomorphism φ:M → End0,1(L) there exists a lattice K containing L as a (0, 1)-sublattice in such a way that the monoid End0,1(K) of all (0, 1)-endomorphisms of K is isomorphic to M, and the restriction to L of every (0, 1)-endomorphism m of K is the (0, 1)-endomorphism φ(m) of L.

Almost free groups were introduced in [9] as groups all of whose “small” subgroups are free. Here “small” means generated by fewer elements than the cardinality of the group. This concept is a generalization of locally free. Suppose κ is a cardinal > ω. A group is κ-free if every subgroup generated by fewer than κ elements is free. A group of cardinality κ which is κ-free is almost free. There are two related concepts which are closer approximations to freeness.

Let K be a number field, K(1) its Hilbert class field, that is, the maximal abelian unramified extension of K, let K(2) be the Hilbert class field of K(1), and let G = Gal(K(2)/K) (alternatively, for p a prime the first and second p class fields enjoy properties analogous to those of the respective class fields discussed in this introduction; the particulars may be found surrounding Lemma 2). Since G/G’ is the largest abelian quotient of G, G/G′ = Gal (K(1))/K) and so G’ is the abelian group Gal(K(2)K(1)); moreover, class field theory provides (Artin) maps φK, φK(1) which are isomorphisms of the class groups Ck, Ck(1) onto G/G′, G′ respectively. In the remarkable paper [1] E. Artin computed the composition VG′

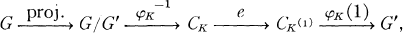
where e is the homomorphism induced on the class groups by extending ideals of K to ideals of K(1), and he gave a formula for computing VG′, the now familiar transfer (Verlagerung) homomorphism, in terms of the group G alone (see Lemma 1).

Let R = ⊕i ≧0Ri be a graded integral domain, and let p ∈ Proj (R) be a homogeneous, relevant prime ideal. Let R(P) = {r/t| r ∈ Ri, t ∈ Ri\p} be the geometric local ring at p and let Rp = {r/t| r ∈ R, t ∈ R\p} be the arithmetic local ring at p. Under the mild restriction that there exists an element r1 ∈ R1\p, W. E. Kuan [2], Theorem 2, showed that r1 is transcendental over R(P) and

where S is the multiplicative system R\p. It is also demonstrated in [2] that R(P) is normal (regular) if and only if Rp is normal (regular). By looking more closely at the relationship between R(P) and R(P), we extend this result to Cohen-Macaulay (abbreviated C M.) and Gorenstein rings.

Ramanujan's well known trigonometrical sum C(m, n) denned by

where x runs through a reduced residue system (mod n), had been shown to occur in analytic problems concerning modular functions of one variable, by Poincaré [4]. Ramanujan, independently later, used these trigonometrical sums in his remarkable work on representation of integers as sums of squares [6]. There are various generalizations of C(m, n) in the literature (some also to algebraic number fields); see, for example, [9] which gives references to some of these. Perhaps the earliest generalization to algebraic number fields is due to H. Rademacher [5]. We here consider a novel generalization involving matrices.

There are relatively few classes of local rings (R, m) for which the question of the rationality of the Poincaré series

where k = R/m, has been settled. (For an example of a local ring with non-rational Poincaré series see the recent paper by D. Anick, “Construction of loop spaces and local rings whose Poincaré—Betti series are nonrational”, C. R. Acad. Sc. Paris 290 (1980), 729-732.) In this note, we compute the Poincaré series of a certain family of local Cohen-Macaulay rings and obtain, as a corollary, the rationality of the Poincaré series of d-dimensional local Gorenstein rings (R, m) of embedding dimension at least e + d – 3, where e is the multiplicity of R. It follows that local Gorenstein rings of multiplicity at most five have rational Poincaré series.

Let RG denote the group ring of a group G over a commutative ring R with unity. We recall that a group is said to be an FC-group if all its conjugacy classes are finite.

In [6], S. K. Sehgal and H. Zassenhaus gave necessary and sufficient conditions for U(RG) to be an FC-group when R is either Z, the ring of rational integers, or a field of characteristic 0.

One of the authors considered this problem for group rings over infinite fields of characteristic p ≠ 2 in [5] and G. Cliffs and S. K. Sehgal [1] completed the study for arbitrary fields. Also, group rings of finite groups over commutative rings containing Z(p), a localization of Z over a prime ideal (p) were studied in [4].

K-coherence (K an integer ≧ –1), has been defined by W. R. R. Transue [3] in such a way that 0-coherence is connectedness and 1-coherence is unicoherence plus local connectedness. It is well-known (see, for instance, [5, p. 82]), that for metric spaces, unicoherence is cyclicly extensible and reducible; furthermore, this result has been generalized by Minear to locally connected spaces, [2, Theorems 4.1 and 4.3]. In this paper we show that for a (k – 1)-coherent and locally (k – 1)-coherent Hausdorff space M,k-coherence is cyclicly extensible and reducible.