Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T06:52:19.787Z Has data issue: false hasContentIssue false
  • English
  • Français

The Two-Sided Factorization of Ordinary Differential Operators

Published online by Cambridge University Press:  20 November 2018

Patrick J. Browne  and
Rodney Nillsen
Patrick J. Browne
Affiliation:
The University of Calgary, Calgary, Alberta
Rodney Nillsen
Affiliation:
The University of Wollongong, Wollongong, New South Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper we shall use I to denote a given interval, not necessarily bounded, of real numbers and Cn to denote the real valued n times continuously differentiable functions on I and C0 will be abbreviated to C. By a differential operator of order n we shall mean a linear function L:Cn → C of the form

1.1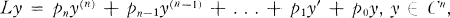

where pn(x) ≠ 0 for x ∊ I and pi ∊ Cj 0 ≦ j ≦ n. The function pn is called the leading coefficient of L.

It is well known (see, for example, [2, pp. 73-74]) thai a differential operator L of order n uniquely determines both a differential operator L* of order n (the adjoint of L) and a bilinear form [·,·]L (the Lagrange bracket) so that if D denotes differentiation, we have for u, v ∊ Cn,

1.2

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 5 , 01 October 1980 , pp. 1045 - 1057
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Coddington, E. A. and Levinson, N., Theory of ordinary differential equations (McGraw-Hill, New York, 1955).Google Scholar
2. Coppel, W. A., Disconjugacy (Lecture Notes in Mathematics, Vol. 220, Springer-Verlag, New York, 1971).CrossRefGoogle Scholar
3. Frobenius, G., Ueber die Déterminante mehrerer Functionen einer Variableln, J. für Math. 77 (1874), 245–257.Google Scholar
4. Heinz, E., Halbbeschrdnktheit gewohnlicher Differentialoperatoren hoherer Ordnung, Math. Ann. 135 (1958), 1–49.Google Scholar
5. Hill, J. M. and Nillsen, R. V., Mutually conjugate solutions of formally self-adjoint differential equations, Proc. Roy. Soc. Edinburgh Ser. A 53 (1979), 93–101.Google Scholar
6. Ince, E. L., Ordinary differential equations (Dover, New York, 1956).Google Scholar
7. Miller, K. S., Linear differential equations in the real domain (Norton, New York, 1963).Google Scholar
8. Pólya, G., On the mean value theorem corresponding to a given linear homogeneous differential equation, Trans. Amer. Math. Soc. 24 (1922), 312–324.Google Scholar
9. Ristroph, R., Pólya's property W and factorization—a short proof, Proc. Amer. Math. Soc. 31 (1972), 631–632.Google Scholar
10. Zettl, A., Factorization of differential operators, Proc. Amer. Math. Soc. 27 (1971), 425–426.Google Scholar
11. Zettl, A., General theory of the factorization of ordinary linear differential operators, Trans. Amer. Math. Soc. 197 (1974), 341–353.Google Scholar