Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T22:54:47.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Weyl Images of Kantor Pairs

Published online by Cambridge University Press:  20 November 2018

Bruce Allison ,
John Faulkner  and
Oleg Smirnov
Bruce Allison
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB, T6G 2G1, Canada e-mail: [email protected]
John Faulkner
Affiliation:
Department of Mathematics, University of Virginia, Kerchof Hall, P.O. Box 400137, Charlottesville, VA, 22904-4137, USA e-mail: [email protected]
Oleg Smirnov
Affiliation:
Department of Mathematics, College of Charleston, Charleston, SC, 29424-0001, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kantor pairs arise naturally in the study of 5-graded Lie algebras. In this article, we introduce and study Kantor pairs with short Peirce gradings and relate themto Lie algebras graded by the root system of type 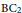$\text{B}{{\text{C}}_{2}}$. This relationship allows us to define so-called Weyl images of short Peirce graded Kantor pairs. We use Weyl images to construct new examples of Kantor pairs, including a class of infinite dimensional central simple Kantor pairs over a field of characteristic 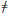$\ne$ 2 or 3, as well as a family of forms of a split Kantor pair of type 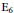${{\text{E}}_{6}}$.

Keywords

17B6017B7017C9917B65Kantor pairgraded Lie algebraJordan pair
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 4 , 01 August 2017 , pp. 721 - 766
Copyright
Copyright © Canadian Mathematical Society 2017

References

[A] Allison, B.,A class of nonassociative algebras with involution containing the class of Jordan algebras. Math. Ann. 237(1978), 133–156. http://dx.doi.Org/10.1007/BF01351677 Google Scholar
[ABG] Allison, B., Benkart, G., and Gao, Y., Lie algebras graded by the root systems BCr, r ≥ 2. Mem. Amer. Math. Soc. 158(2002), no. 751.Google Scholar
[AF1] Allison, B. and Faulkner, J., Elementary groups and invertibility for Kantor pairs. Comm. Algebra 27(1999), 519–556.http://dx.doi.org/10.1080/00927879908826447 Google Scholar
[AF2] Allison, B. and Faulkner, J., Dynkin diagrams and short Peirce gradings of Kantor pairs. arxiv:1703.04055v1 Google Scholar
[ADG] Aranda-Orna, D., Draper, C., and Guido, V., Weyl groups of some fine gradings on e6. J. Algebra 417(2014), 333–390.http://dx.doi.Org/10.1016/j.jalgebra.2O14.07.001 Google Scholar
[At] Atsuyama, K., On the algebraic structures of graded Lie algebras of second order. Kodai Math. J. 5(1982), 225–229.http://dx.doi.org/10.2996/kmj71138036551 Google Scholar
[BN] Benkart, G. and Neher, E., The centroid of extended affme and root graded Lie algebras. J. Pure Appl. Algebra 205(2006), 117–145.http://dx.doi.Org/10.101 6/j.jpaa.2005.06.007 Google Scholar
[BS] Benkart, G. and Smirnov, O., Lie algebras graded by the root system BC1. J. Lie Theory 13(2003), 91–132.Google Scholar
[BDDRE] Borsten, L., Dahanayake, D., Duff, M. J., Rubens, W., and Ebrahim, H., Freudenthal triple classification of three-qubit entanglement, Phys. Rev. A 80(2009), 032326.http://dx.doi.org/10.1103/PhysRevA.80.032326 Google Scholar
[Bl] Bourbaki, N., Elements of mathematics. Algebra, Part I. Translated from the French. Hermann, Paris, 1974.Google Scholar
[B2] Bourbaki, N., Commutative algebra. Chapters 1-7. Translated from the French. Springer-Verlag, Berlin, 1998.Google Scholar
[B3] Bourbaki, N., Elements of Mathematics. Lie groups and Lie algebras. Chapters 4-6. Translated from the French. Springer-Verlag, Berlin, 2002.http://dx.doi.org/10.1007/978-3-540-89394-3 Google Scholar
[C] Cartan, É., Sur la structure des groups de transformations finis et continues. Thése, Paris, Nony 1894. In: Œuvres complétes, Partie I, Groupes de Lie. Gauthier-Villars, Paris, 1952, pp. 137–287.Google Scholar
[D] Djokovic, D., Classification ofL-graded real semisimple Lie algebras. J. Algebra 76(1982), 367–382.http://dx.doi.Org/10.1016/0021-8693(82)90220-4 Google Scholar
[E] Elduque, A., The magie square and symmetric compositions. II Rev. Mat. Iberoam. 23(2007), 57–84.http://dx.doi.org/10.4171/RMI/486 Google Scholar
[EK] Elduque, A. and Kochetov, M., Gradings on simple Lie algebras. Mathematical Surveys and Monographs, 189. American Mathematical Society, Providence, RI, 2013.Google Scholar
[EO] Elduque, A. and Okubo, S., Special Freudenthal-Kantor triple systems and Lie algebras with dicyclic symmetry. Proc. Roy. Soc. Edinburgh Sect. A 141(2011), 1225–1262.http://dx.doi.Org/10.1017/S0308210510000569 Google Scholar
[EKO] Elduque, A., Kamiya, N. and Okubo, S., Left unital Kantor triple systems and structurable algebras. Linear Multilinear Algebra 62(2014), no. 10,1293–1313.http://dx.doi.org/10.1080/03081087.2013.825909 Google Scholar
[F] Faulkner, J., Some forms of exceptional Lie algebras. Comm. Algebra, 42(2014), 4854–4873.http://dx.doi.org/10.1080/00927872.2013.822878 Google Scholar
[FF] Faulkner, J. and Ferrar, J., On the structure of symplectic ternary algebras. Nederl. Akad. Wetensch. Proc. Ser. A 75=Indag. Math. 34(1972), 247–256.http://dx.doi.Org/10.1016/1385-7258(72)90062-5 Google Scholar
[GLN] Garcia, E., Gomez Lozano, M., and Neher, E., Nondegeneracy for Lie triple systems and Kantor pairs. Canad. Math. Bull. 54 (2011), 442–455.http://dx.doi.Org/10.4153/CMB-2O11-023-9 Google Scholar
[GN] Garcia, E. and Neher, E., Tits-Kantor-Koecher superalgebras of Jordan superpairs covered by grids. Comm. Algebra 31(2003), 3335–3375. http://dx.doi.org/10.1081/ACB-120022230 Google Scholar
[G] Günaydin, M., Extended superconformai symmetry, Freudenthal triple systems and gauged WZW models. Springer Lecture Notes in Physics 447(1995), 54–69.http://dx.doi.Org/10.1007/3-540-59163-X_255 Google Scholar
[GOV] V. V.Gorbatsevich, , Onischhik, A. L., and Vinberg, E. B., Structure of Lie groups and Lie algebras. In: Lie groups and Lie algebras III, Encyclopaedia Math. Sci., 41. Springer-Verlag, Berlin, 1994. http://dx.doi.org/= 10.1007/978-3-662-03066-0 Google Scholar
[H] Humphreys, J. E., Introduction to Lie algebras and representation theory. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1972.Google Scholar
[Jl] Jacobson, N., General representation theory of Jordan algebras. Trans. Amer. Math. Soc. 70(1951), 509–530.http://dx.doi.org/10.1090/S0002-9947-1951-0041118-9 Google Scholar
[J2] Jacobson, N., Structure of rings. American Mathematical Society, Colloquium Publications, 37. American Mathematical Society, Providence. RI, 1956.Google Scholar
[J3] Jacobson, N., Lie algebras. Interscience Publishers, New York, 1962.Google Scholar
[Kl] Kantor, I. L., Certain generalizations of Jordan algebras (Russian). Trudy Sem. Vektor. Tenzor. Anal. 16(1972), 407–499.Google Scholar
[K2] Kantor, I. L., Models of exceptional Lie algebras. Soviet Math. Dokl. 14(1973), 254–258.Google Scholar
[KS] Kantor, I.L. and Skopec, I. M., Freudenthal trilinear operations (Russian). Trudy. Sem. Vektor. Tenzor. Anal. 18(1978), 250–263 Google Scholar
[L-G] Leedham-Green, C. R., The class group of Dedekind domains. Trans. Amer. Math. Soc. 163(1972), 493–500.http://dx.doi.org/10.1090/S0002-9947-1972-0292806-4 Google Scholar
[L] Loos, O., Jordan pairs. Lecture Notes in Mathematics, 460. Springer-Verlag, Berlin, 1975.Google Scholar
[LN] Loos, O. and Neher, E., Steinberg groups for Jordan pairs. C. R. Math. Acad. Sci. Paris 348(2010), 839–842.http://dx.doi.Org/10.1016/j.crma.2O10.07.012 Google Scholar
[LB] Fernandez Lopez, A. and Tocon Barroso, M., Strongly prime Jordan pairs with nonzero socle. ManuscriptaMath. 111(2003), 321–340. http://dx.doi.org/10.1007/s00229-003-0372-6 Google Scholar
[MQSTZ] Marrani, A., Qiu, C., Shih, S. D., Tagliaferro, A., and Zumino, B., Freudenthal gauge theory. J. High Energy Phys. (2013).Google Scholar
[Mc] McCrimmon, K, A taste of Jordan algebras. Springer-Verlag, New York, 2004.Google Scholar
[M] Meyberg, K., Eine Theorie der Freudenthalschen Tripelsysteme. I, II. Nederl. Akad. Wetensch. Proc. Ser. A 71=Indag. Math. 30(1968), 162-174, 175–190. http://dx.doi.org/10.1016/S1 385-7258(68)5001 8-0 Google Scholar
[Na] Narkiewicz, W., Elementary and analytic theory of algebraic numbers. Third edition. Springer-Verlag, Berlin, 2004.http://dx.doi.org/10.1007/978-3-662-07001-7 Google Scholar
[Nl] Neher, E., Involutive gradings in Jordan structures, Comm. Algebra 9(1981), 575–599.http://dx.doi.Org/10.1080/0092 7878108822603 Google Scholar
[N2] Neher, E., Lie algebras graded by 3-graded root systems and Jordan pairs covered by grids. J. Algebra 140(1991), 284–329.Google Scholar
[Sel] Seligman, G. B., Modular Lie algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete, 40.Springer-Verlag,New York 1967.Google Scholar
[Ser] Serre, J.P., Galois cohomology. Springer-Verlag, Berlin 2002.Google Scholar
[Sm] Smirnov, O., Simple and semisimple structurable algebras. Algebra and Logic 29(1990), 377–394.Google Scholar
[St] Steinberg, R., Automorphisms of classical Lie algebras. Pacific J. Math. 11(1961), 1119–1129.http://dx.doi.Org/10.2140/pjm.1961.11.1119 Google Scholar
[YA] Yamaguti, K. and Asano, H., On the Freudenthal*s construction of exceptional Lie algebras. Proc. Japan Acad. 51(1975), 253–258.http://dx.doi.Org/10.3792/pja/1195518629 Google Scholar
[YO] Yamaguti, K. and Ono, A., On representations of Freudenthal-Kantor triple systems U(∊,δ). Bull. Fac. School Ed. Hiroshima Univ. Part II 7(1984), 43–51.Google Scholar
[Zl] Zelmanov, E., Primary Jordan triple systems II. Sibirskii Math. Zh. 25(1984), 50–61.http://dx.doi.org/10.1007/BF00969508 Google Scholar
[Z2] Zelmanov, E., Lie algebras with a finite grading, Math. USSR-Sb. 52(1985), 347–385.Google Scholar