Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T07:12:14.745Z Has data issue: false hasContentIssue false
  • English
  • Français

Wedge Operations and Torus Symmetries II

Published online by Cambridge University Press:  20 November 2018

Suyoung Choi  and
Hanchul Park
Suyoung Choi
Affiliation:
Department of Mathematics, Ajou University, 206, World cup-ro, Yeongtong-gu, Suwon, 443-749, Republic of Korea e-mail: [email protected]
Hanchul Park
Affiliation:
School of Mathematics, Korea Institute for Advanced Study (KIAS), 85 Hoegiro Dongdaemun-gu, Seoul 130-277, Republic of Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A fundamental idea in toric topology is that classes of manifolds with well-behaved torus actions (simply, toric spaces) are classified by pairs of simplicial complexes and (non-singular) characteristic maps. In a previous paper, the authors provided a new way to find all characteristic maps on a simplicial complex 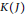$K(J)$ obtainable by a sequence of wedgings from 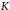$K$.The main idea was that characteristic maps on 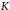$K$ theoretically determine all possible characteristic maps on a wedge of 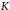$K$.

We further develop our previous work for classification of toric spaces. For a star-shaped simplicial sphere 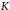$K$ of dimension 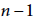$n-1$ with 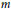$m$ vertices, the Picard number Pic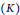$(K)$ of 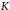$K$ is 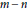$m-n$. We call 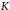$K$ a seed if 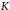$K$ cannot be obtained by wedgings. First, we show that for a fixed positive integer 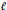$\ell $, there are at most finitely many seeds of Picard number 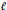$\ell $ supporting characteristic maps. As a corollary, the conjecture proposed by V. V. Batyrev in is solved affirmatively.

Secondly, we investigate a systematicmethod to find all characteristic maps on 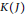$K(J)$ using combinatorial objects called (realizable) puzzles that only depend on a seed 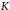$K$. These two facts lead to a practical way to classify the toric spaces of fixed Picard number.

Keywords

57S2514M2552B1113F5518A10puzzletoric varietysimplicial wedgecharacteristic map
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 4 , 01 August 2017 , pp. 767 - 789
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bahri, A., Bendersky, M., Cohen, F. R., and Gitler, S., Operations on polyhedral products and a new topological construction of infinite families oftoric manifolds. Homology Homotopy Appl. 17(2015), no. 2, 137–160.http://dx.doi.org/10.4310/HHA.2015.v17.n2.a8 Google Scholar
[2] Batyrev, V. V., On the classification of smooth projective toric varieties. Tohoku Math. J. (2) 43(1991), no. 4, 569–585.http://dx.doi.org/10.2748/tmjV11 78227429 Google Scholar
[3] Buchstaber, V. M. and Panov, T. E., Torus actions and their applications in topology and combinatorics. University Lecture Series, 24. American Mathematical Society, Providence, RI, 2002.Google Scholar
[4] Choi, S. and Park, H., Wedge operations and torus symmetries. Tohoku Math. J. (2), 68(2016), no. 1,91–138.http://dx.doi.org/10.2748/tmj71458248864 Google Scholar
[5] Choi, S., Wedge operations and a new family of projective toric manifolds. To appear in Israel J. Math. arxiv:1 507.08919. Google Scholar
[6] Erokhovets, N., Buchstaber invariant of simple polytopes. Russian Math. Surveys 63(2008), no. 5, 962–964 (Russian),http://dx.doi.org/10.4213/rm9231 Google Scholar
[7] Grünbaum, B., Convex polytopes. Second ed. Graduate Texts in Mathematics, 221. Springer-Verlag, New York, 2003.Google Scholar
[8] Kleinschmidt, P.,A classification oftoric varieties with few generators. Aequationes Math. 35(1988), no. 2-3, 254–266.http://dx.doi.Org/10.1007/BF01830946 Google Scholar
[9] Kleinschmidt, P. and Sturmfels, B., Smooth toric varieties with small Picard number are projective. Topology 30(1991), no. 2, 289–299.http://dx.doi.Org/10.1016/0040-9383(91 )90015-V Google Scholar
[10] Mani, P., Spheres with few vertices. J. Combinatorial Theory Ser. A 13(1972), 346–352. http://dx.doi.Org/10.1016/0097-315(72)90068-4 Google Scholar
[11] Oda, T., Convex bodies and algebraic geometry. Ergebnisse der Mathematik und ihrer Grenzgebiete(3), 15. Springer-Verlag, Berlin, 1988.Google Scholar