Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Haimo, Deborah Tepper
1965.
Integral equations associated with Hankel convolutions.
Transactions of the American Mathematical Society,
Vol. 116,
Issue. 0,
p.
330.


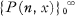 be the family of orthonormal polynomials associated with a, so that
be the family of orthonormal polynomials associated with a, so that

