Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-02T22:39:01.536Z Has data issue: false hasContentIssue false
  • English
  • Français

Unit Preserving Isometries are Homomorphisms in Certain Lp

Published online by Cambridge University Press:  20 November 2018

Robert Schneider
Robert Schneider*
Affiliation:
Lehman College, Bronx, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

(a) (ᓂ1 and ᓂ2 will always denote positive bounded measures of equal mass defined on sets X and F respectively. Lp(ᓂ1) and Lp(ᓂ2) will always be complex Lp spaces.

(b) M C L∞(ᓂ1) will always denote a subalgebra of L∞(ᓂ1) containing constants.

(c) Let 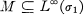be a 1 inear map of ikf into Lp(ᓂ2). We shall say that T is a linear isometry in LP norm if

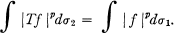
We shall prove the following:

THEOREM B. If 2 < p < ∞ and 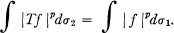is a linear isometry in the Lp norm with T(l) = 1 then T is a homomorphism on M; that is

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 133 - 137
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Forelli, F., The isometries of HP, Can. J. Math. 16 (1964), 721–728.Google Scholar
2. Forelli, F., A theorem on isometries and the application of it to the isometries of HP(S) for 2 < p < ∞, Can. J. Math. 25 (1973), 284–289.Google Scholar
3. Hoffman, K., Banach spaces of analytic functions (Prentice Hall, Englew∞d Cliffs, N.J., 1962).Google Scholar