Article contents
Torsion in thin regions of Khovanov homology
Published online by Cambridge University Press: 29 January 2021
Abstract
In the integral Khovanov homology of links, the presence of odd torsion is rare. Homologically thin links, that is, links whose Khovanov homology is supported on two adjacent diagonals, are known to contain only 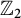 $\mathbb {Z}_2$
torsion. In this paper, we prove a local version of this result. If the Khovanov homology of a link is supported on two adjacent diagonals over a range of homological gradings and the Khovanov homology satisfies some other mild restrictions, then the Khovanov homology of that link has only
$\mathbb {Z}_2$
torsion. In this paper, we prove a local version of this result. If the Khovanov homology of a link is supported on two adjacent diagonals over a range of homological gradings and the Khovanov homology satisfies some other mild restrictions, then the Khovanov homology of that link has only 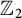 $\mathbb {Z}_2$
torsion over that range of homological gradings. These conditions are then shown to be met by an infinite family of three-braids, strictly containing all three-strand torus links, thus giving a partial answer to Sazdanović and Przytycki’s conjecture that three-braids have only
$\mathbb {Z}_2$
torsion over that range of homological gradings. These conditions are then shown to be met by an infinite family of three-braids, strictly containing all three-strand torus links, thus giving a partial answer to Sazdanović and Przytycki’s conjecture that three-braids have only 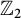 $\mathbb {Z}_2$
torsion in Khovanov homology. We use these computations and our main theorem to obtain the integral Khovanov homology for all links in this family.
$\mathbb {Z}_2$
torsion in Khovanov homology. We use these computations and our main theorem to obtain the integral Khovanov homology for all links in this family.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
AC was supported in part by the project P31705 of the Austrian Science Fund. AL was supported in part by NSF grant DMS-1811344. RS was supported in part by the Simons Foundation Collaboration Grant 318086 and NSF Grant DMS 1854705.
References
- 1
- Cited by



