Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T06:15:36.706Z Has data issue: false hasContentIssue false
  • English
  • Français

The Supersingular Locus of the Shimura Variety for GU(1, s)

Published online by Cambridge University Press:  20 November 2018

Inken Vollaard
Inken Vollaard*
Affiliation:
Mathematisches Institut, Universität Bonn, Beringstr. 1, 53115 Bonn, Germany (Current address) c/o TorstenWedhorn, Institut fürMathematik, Universität Paderborn, Warburger Str. 100, 33098 Paderborn, Germany, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

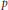In this paper we study the supersingular locus of the reduction modulo $p$ of the Shimura variety for 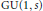$\text{GU}\left( 1,\,s \right)$ in the case of an inert prime 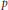$p$. Using Dieudonné theory we define a stratification of the corresponding moduli space of 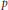$p$-divisible groups. We describe the incidence relation of this stratification in terms of the Bruhat–Tits building of a unitary group.

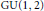In the case of $\text{GU}\left( 1,\,2 \right)$, we show that the supersingular locus is equidimensional of dimension 1 and is of complete intersection. We give an explicit description of the irreducible components and their intersection behaviour.

Keywords

14G3511G1814K10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 3 , 01 June 2010 , pp. 668 - 720
Copyright
Copyright © Canadian Mathematical Society 2010

References

[BG] Bachmat, E. and Goren, E. Z., On the non-ordinary locus in Hilbert-Blumenthal surfaces. Math. Ann. 313(1999), no. 3, 475–506. doi:10.1007/s002080050270 Google Scholar
[BW] Bültel, O. and Wedhorn, T., Congruence relations for Shimura varieties associated to some unitary groups. J. Inst. Math. Jussieu 5(2006), 229–261.Google Scholar
[DL] Deligne, P. and Lusztig, G., Representations of reductive groups over finite fields. Ann. of Math. 103(1976), no. 1, 103–161. doi:10.2307/1971021 Google Scholar
[Gn] Goren, E. Z., Hilbert modular varieties in positive characteristic. In: The Arithmetic and Geometry of Algebraic Cycles. CR M Proc Lecture Notes 24, American Mathematical Society, Providence, RI, 2000, pp. 283–303.Google Scholar
[GO] Goren, E. Z. and Oort, F., Stratifications of Hilbert modular varieties. J. Algebraic Geom. 9(2000), no. 1, 111–154.Google Scholar
[Ka] Kaiser, C., Ein getwistetes fundamentales Lemma für die GSp4. Bonner Mathematische Schriften 303. Universität Bonn, Mathematisches Institut, 1997.Google Scholar
[KO1] Katsura, T., Oort, F., Supersingular abelian varieties of dimension two or three and class numbers. In: Algebraic Geometry. Adv. Stud. Pure Math. 10, North-Holland, Amsterdam, 1987, pp. 253–281.Google Scholar
[KO2] Katsura, T., Families of supersingular abelian surfaces. Compositio Math. 62(1987), no. 2, 107–167.Google Scholar
[Kb] Koblitz, N., p-adic variation of the zeta-function over families of varieties defined over finite fields. Compositio Math. 31(1975), no. 2, 119–218.Google Scholar
[K1] Kottwitz, R. E.. Stable trace formula: cuspidal tempered terms. Duke Math. J. 51(1984), no. 3, 611–650. doi:10.1215/S0012-7094-84-05129-9 Google Scholar
[K2] Kottwitz, R. E., Points on some Shimura varieties over finite fields. J. Amer. Math. Soc. 5(1992), 373–444. doi:10.2307/2152772 Google Scholar
[KR1] Kudla, S. S. and Rapoport, M., Arithmetic Hirzebruch-Zagier cycles. J. Reine Angew. Math. 515(1999), 155–244.Google Scholar
[KR2] Kudla, S. S. and Rapoport, M., Cycles on Siegel threefolds and derivatives of Eisenstein series. Ann. Sci. École Norm. Sup. 33(2000), no. 5, 695–756.Google Scholar
[LO] Li, K.-Z. and Oort, F., Moduli of supersingular abelian varieties. Lecture Notes in Mathematics 1680, Springer-Verlag, Berlin, 1998.Google Scholar
[Lu1] Lusztig, G., Coxeter orbits and eigenspaces of Frobenius. Invent. Math. 38(1976), no. 2, 101–159. doi:10.1007/BF01408569 Google Scholar
[Lu2] Lusztig, G., On the finiteness of the number of unipotent classes. Invent. Math. 34(1976), no. 3, 201–213. doi:10.1007/BF01403067 Google Scholar
[Ri] Richartz, M.: Klassifikation von selbstdualen Dieudonnégittern in einem dreidimensionalen polarisierten supersingulären Isokristall. Bonner Mathematische Schriften 311, Universitát Bonn, 1998.Google Scholar
[RZ] Rapoport, M. and Zink, T., Period spaces for p-divisible groups. Annals of Mathematics Studies 141, Princeton University Press, Princeton, NJ, 1996.Google Scholar
[St] Stamm, H., On the reduction of the Hilbert-Blumenthal-moduli scheme with ¡0(p)-level structure. Forum Math. 9(1997), no. 4, 405–455. doi:10.1515/form.1997.9.405 Google Scholar
[Ti] Tits, J., Reductive groups over local fields. In: Automorphic Forms, Representations and L-Functions. Proc. Sympos. Pure Math. 33, American Mathematical Society, Providence, RI, 1979, pp. 29–69.Google Scholar
[Yu] Yu, C.-F., On the supersingular locus in Hilbert-Blumenthal 4-folds. J. Algebraic Geom. 12(2003), no.4, 653–698.Google Scholar
[Zi1] Zink, T., Cartiertheorie kommutativer formaler Gruppen. Teubner-Texte zur Mathematik 68. GB., Teubner Verlagsgessellschaft, Leipzig, 1984.Google Scholar
[Zi2] Zink, T., The display of a formal p-divisible group. In: Cohomologies p-adiques et applications arithmétiques, I. Astérisque No. 278 (2002), 127–248.Google Scholar