Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-03T00:38:58.070Z Has data issue: false hasContentIssue false
  • English
  • Français

Structural Properties of Elementary Operators

Published online by Cambridge University Press:  20 November 2018

Constantin Apostol  and
Lawrence Fialkow
Constantin Apostol
Affiliation:
Arizona State University, Tempe, Arizona
Lawrence Fialkow
Affiliation:
Arizona State University, Tempe, Arizona
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

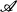Let and 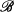denote complex Banach algebras and let 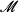b e a left Banach 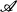module and a right Banach 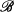-module. If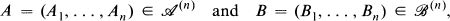

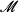we define the bounded linear elementary operator R(A, B), acting on , by

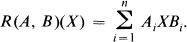
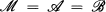For the case , elementary operators were introduced by Lumer and Rosenblum [19], who studied their spectral properties. In this setting many authors subsequently studied spectral, algebraic, metric, and structural properties of elementary operators, with particular attention devoted to the inner derivations δa (δa(x) = ax – xa) [25], generalized derivations τ(a, b) (τ(a, b)(x) = ax – xb) [9, 10], and elementary multiplications S(a, b) (S(a, b)(x) = axb), including left and right multiplications La and Rb [11].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 6 , 01 December 1986 , pp. 1485 - 1524
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Apostol, C., Quasithangularity in Hilbert space, Indiana Univ. Math. J. 22 (1973), 817–825.Google Scholar
2. Apostol, C., The correction by compact perturbation of the singular behavior of operators, Rev. Roum. Math. Pures et Appl. 21 (1976), 155–175.Google Scholar
3. Brown, A. and Pearcy, C., Compact restrictions of operators, Acta. Sci. Math. 32 (1971), 271–282.Google Scholar
4. Brown, A., Pearcy, C. and Salinas, N., Ideals of compact operators on Hilbert space, Michigan Math. J. 18 (1971), 373–384.Google Scholar
5. Calkin, J. W., Two-sided ideals and congruences in the ring of bounded operators in Hilbert space, Ann. of Math. 42 (1941), 839–873.Google Scholar
6. Colojoara, I. and Foias, C., Theory of generalized spectral operators (Gordon and Breach, New York, 1968).Google Scholar
7. Davis, C. and Rosenthal, P., Solving linear operator equations, Can. J. Math. 26 (1974), 1384–1389.Google Scholar
8. Douglas, R. G., Banach algebra techniques in operator theory (Academic Press, New York and London, 1972).Google Scholar
9. Fialkow, L. A., A note on the operator X → AX — XB, Trans. Amer. Math. Soc. 243 (1978), 147–168.Google Scholar
10. Fialkow, L. A., Elements of spectral theory for generalized derivations, J. Operator Theory 3 (1980), 89–113.Google Scholar
11. Fialkow, L. A., Spectral properties of elementary operators, Acta Sci. Math. 46 (1983), 269–282.Google Scholar
12. Fialkow, L. A., Spectral properties of elementary operators II, Trans. Amer. Math. Soc. 290 (1985), 415–429.Google Scholar
13. Fialkow, L. A., The index of an elementary operator, Indiana University Math. J. 35 (1986), 73–102.Google Scholar
14. Fialkow, L. A. and Loebl, R., Elementary mappings into ideals of operators, Illinois J. Math. 25 (1984), 555–578.Google Scholar
15. Fong, C. K. and Sourour, A. R., On the operator identity Σ AkXBk = 0, Can. J. Math. 31 (1979), 845–857.Google Scholar
16. Gohberg, I. C. and Krein, M. G., Introduction to the theory of linear nonselfadjoint operators, Transi. Math. Monographs 18 (Amer. Math. Soc, Providence, R.I., 1969).Google Scholar
17. Harte, R., Tensor products, multiplication operators and the spectral mapping theorem, Proc. Royal Irish Acad. 73A (1973), 285–302.Google Scholar
18. Herrero, D. A., Approximation of Hilbert space operators I, Research Notes in Math. 72 (Pitman Books Ltd, 1982).Google Scholar
19. Lumer, G. and Rosenblum, M., Linear operator equations, Proc. Amer. Math. Soc. 10 (1959), 32–41.Google Scholar
20. Olsen, C. L., A structure theorem for polynomially compact operators, Amer. J. Math. 93 (1971), 686–698.Google Scholar
21. Radjavi, H. and Rosenthal, P., Invariant subspaces (Springer-Verlag, 1973).CrossRefGoogle Scholar
22. Rickart, C. E., Banach algebras (D. Van Nostrand Co., Princeton, 1960).Google Scholar
23. Riesz, F. and Sz.-Nagy, B., Functional analysis (Ungar, New York, 1955).Google Scholar
24. Schatten, R., Norm ideals of completely continuous operators (Springer-Verlag, Berlin, 1960).CrossRefGoogle Scholar
25. Stampfli, J., The norm of a derivation. Pacific J. Math. 33 (1970), 737–747.Google Scholar
26. Stampfli, J., Derivations on B(H): The range, Illinois J. Math. 17 (1973), 518–524.Google Scholar
27. Voiculescu, D., A non-commutative Weyl-von Neumann theorem, Rev. Roumaine Math. Pures Appl. 21 (1976), 97–113.Google Scholar
28. Zelasko, W., On a certain class of non-removable ideals in Banach algebras, Stud. Math. 44 (1972), 87–92.Google Scholar