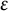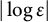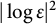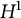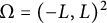1 Introduction
1.1 The Ginzburg-Landau equations in the London limit
The Ginzburg-Landau (GL) energy is used to describe the behavior of type-II superconductors. In 2D, this energy can be written as
Here,
![]() ${{\Omega }}\subset \mathbb {R}^2$
is a smooth simply-connected bounded domain,
${{\Omega }}\subset \mathbb {R}^2$
is a smooth simply-connected bounded domain,
![]() ${\varepsilon }>0$
is a small parameter (the inverse of the GL parameter),
${\varepsilon }>0$
is a small parameter (the inverse of the GL parameter),
![]() $h_{\operatorname {\mathrm {\text {ex}}}}>0$
is another parameter representing the exterior magnetic field, and
$h_{\operatorname {\mathrm {\text {ex}}}}>0$
is another parameter representing the exterior magnetic field, and
![]() $A:=(A_1,A_2):{{\Omega }}\rightarrow \mathbb {R}^2$
is the vector-potential of the induced magnetic field which is obtained by
$A:=(A_1,A_2):{{\Omega }}\rightarrow \mathbb {R}^2$
is the vector-potential of the induced magnetic field which is obtained by
![]() $h=\mathrm {curl\,} A:= \partial _1A_2-\partial _2 A_1$
. It is sometimes more convenient to see A as a
$h=\mathrm {curl\,} A:= \partial _1A_2-\partial _2 A_1$
. It is sometimes more convenient to see A as a
![]() $1$
-form
$1$
-form
![]() $A=A_1 dx_1+A_2 dx_2$
in
$A=A_1 dx_1+A_2 dx_2$
in
![]() $\mathbb {R}^2$
and h as a
$\mathbb {R}^2$
and h as a
![]() $2$
-form
$2$
-form
![]() $h= d A$
. We will use both points of view in the following. The complex function
$h= d A$
. We will use both points of view in the following. The complex function
![]() $u:{{\Omega }}\rightarrow \mathbb {C}$
is called the order parameter. The regions where
$u:{{\Omega }}\rightarrow \mathbb {C}$
is called the order parameter. The regions where
![]() $|u| \simeq 1$
are in a superconducting phase, whereas the regions where
$|u| \simeq 1$
are in a superconducting phase, whereas the regions where
![]() $|u|\simeq 0$
are in a normal phase. The covariant gradient
$|u|\simeq 0$
are in a normal phase. The covariant gradient
![]() $\nabla _A u=(\nabla -iA)u$
is a vector in
$\nabla _A u=(\nabla -iA)u$
is a vector in
![]() $\mathbb {C}^2$
whose coordinates are
$\mathbb {C}^2$
whose coordinates are
![]() $ (\partial _1^Au,\partial _2^Au)=(\partial _1 u-iA_1u,\partial _2 u-iA_2u)$
. The limit
$ (\partial _1^Au,\partial _2^Au)=(\partial _1 u-iA_1u,\partial _2 u-iA_2u)$
. The limit
![]() ${\varepsilon }\rightarrow 0$
corresponds to extreme type-II materials, and this is the regime we consider in this article. Critical points of
${\varepsilon }\rightarrow 0$
corresponds to extreme type-II materials, and this is the regime we consider in this article. Critical points of
![]() $\mathrm {GL}_{\varepsilon }$
in the space
$\mathrm {GL}_{\varepsilon }$
in the space
are points
![]() $ (u,A)\in X$
such that
$ (u,A)\in X$
such that
 $$ \begin{align} \mathrm{d} \mathrm{GL}_{\varepsilon}(u,A,v,B)&:= \frac{\mathrm{d} }{\mathrm{d} t}\Big|_{t=0}\mathrm{GL}_{\varepsilon}(u+tv,A+tB)=0, \notag\\&\quad\text{ for all} \ (v,B)\in {\mathcal C}^{\infty}(\overline{{{\Omega}}},\mathbb{C})\times {\mathcal C}^{\infty}_c(\mathbb{R}^2,\mathbb{R}^2). \end{align} $$
$$ \begin{align} \mathrm{d} \mathrm{GL}_{\varepsilon}(u,A,v,B)&:= \frac{\mathrm{d} }{\mathrm{d} t}\Big|_{t=0}\mathrm{GL}_{\varepsilon}(u+tv,A+tB)=0, \notag\\&\quad\text{ for all} \ (v,B)\in {\mathcal C}^{\infty}(\overline{{{\Omega}}},\mathbb{C})\times {\mathcal C}^{\infty}_c(\mathbb{R}^2,\mathbb{R}^2). \end{align} $$
They satisfy the Euler-Lagrange equations
 $$ \begin{align} \left\{ \begin{array}{@{}r@{\ }c@{\ }ll} -(\nabla_A)^2u&=&\frac{u}{{\varepsilon}^2}(1-|u|^2) &\text{ in } {{\Omega}} \\ -\nabla^{\perp} h&=&\langle iu,\nabla_A u \rangle & \text{ in } {{\Omega}} \\ h&=& h_{\operatorname{\mathrm{\text{ex}}}} & \text{ in } \mathbb{R}^2\setminus {{\Omega}} \\ \nu \cdot \nabla_A u & =& 0 & \text{ on } \partial {{\Omega}}. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{@{}r@{\ }c@{\ }ll} -(\nabla_A)^2u&=&\frac{u}{{\varepsilon}^2}(1-|u|^2) &\text{ in } {{\Omega}} \\ -\nabla^{\perp} h&=&\langle iu,\nabla_A u \rangle & \text{ in } {{\Omega}} \\ h&=& h_{\operatorname{\mathrm{\text{ex}}}} & \text{ in } \mathbb{R}^2\setminus {{\Omega}} \\ \nu \cdot \nabla_A u & =& 0 & \text{ on } \partial {{\Omega}}. \end{array} \right. \end{align} $$
Here, the covariant Laplacian is defined by
![]() $ (\nabla _A)^2u=\partial _1^A(\partial _1^Au)+\partial _2^A(\partial _2^Au)$
, and
$ (\nabla _A)^2u=\partial _1^A(\partial _1^Au)+\partial _2^A(\partial _2^Au)$
, and
![]() $ \langle iu,\nabla _Au\rangle $
is a vector in
$ \langle iu,\nabla _Au\rangle $
is a vector in
![]() $\mathbb {R}^2$
whose coordinates are
$\mathbb {R}^2$
whose coordinates are
![]() $ (\langle iu,\partial _1^Au\rangle ,\langle iu,\partial _2^Au\rangle )$
where, for two complex numbers
$ (\langle iu,\partial _1^Au\rangle ,\langle iu,\partial _2^Au\rangle )$
where, for two complex numbers
![]() $z,w\in \mathbb {C}$
, we have denoted by
$z,w\in \mathbb {C}$
, we have denoted by
![]() $ \langle z,w\rangle $
the quantity
$ \langle z,w\rangle $
the quantity
![]() $ \frac 12 (z\bar {w}+w\bar {z})$
. We also use the notation
$ \frac 12 (z\bar {w}+w\bar {z})$
. We also use the notation
![]() $\nabla ^{\perp } h=(-\partial _2h,\partial _1h)$
, and
$\nabla ^{\perp } h=(-\partial _2h,\partial _1h)$
, and
![]() $\nu $
denotes the outward unit normal to
$\nu $
denotes the outward unit normal to
![]() $\partial {{\Omega }}$
.
$\partial {{\Omega }}$
.
We observe that Equation (1.4) and the energy
![]() $\mathrm {GL}_{\varepsilon }$
are invariant under gauge transformations. More precisely, if
$\mathrm {GL}_{\varepsilon }$
are invariant under gauge transformations. More precisely, if
![]() $(u,A)$
satisfies (1.4), then for any
$(u,A)$
satisfies (1.4), then for any
![]() $f \in H^2_{\text {loc}}(\mathbb {R}^2,\mathbb {R})$
, the couple
$f \in H^2_{\text {loc}}(\mathbb {R}^2,\mathbb {R})$
, the couple
![]() $(ue^{if},A+\nabla f)$
also satisfies (1.4) and
$(ue^{if},A+\nabla f)$
also satisfies (1.4) and
![]() $\mathrm {GL}_{\varepsilon }(ue^{if},A+\nabla f)=\mathrm {GL}_{\varepsilon } (u,A)$
. Physically, only the gauge-invariant quantities are relevant; these are, for example,
$\mathrm {GL}_{\varepsilon }(ue^{if},A+\nabla f)=\mathrm {GL}_{\varepsilon } (u,A)$
. Physically, only the gauge-invariant quantities are relevant; these are, for example,
![]() $\mathrm {GL}_{\varepsilon }$
the energy,
$\mathrm {GL}_{\varepsilon }$
the energy,
![]() $|u|$
the local density of superconducting electrons pairs (in the Barden-Cooper-Schrieffer theory), h the induced magnetic field, and
$|u|$
the local density of superconducting electrons pairs (in the Barden-Cooper-Schrieffer theory), h the induced magnetic field, and
![]() $j:=\langle iu,\nabla _Au\rangle $
the current vector. In order to deal with this gauge-invariance, one often works in the so-called Coulomb gauge by requiring
$j:=\langle iu,\nabla _Au\rangle $
the current vector. In order to deal with this gauge-invariance, one often works in the so-called Coulomb gauge by requiring
 $$ \begin{align} \left\{ \begin{array}{@{}r@{\ }c@{\ }ll} \mathrm{div} A &=& 0 & \text{ in } {{\Omega}} \\ A\cdot \nu &=& 0 &\text{ on } \partial {{\Omega}}. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{@{}r@{\ }c@{\ }ll} \mathrm{div} A &=& 0 & \text{ in } {{\Omega}} \\ A\cdot \nu &=& 0 &\text{ on } \partial {{\Omega}}. \end{array} \right. \end{align} $$
It can be shown that if
![]() $ (u,A)$
is in X and satisfies (1.4), and if A is in the Coulomb gauge (1.5), then
$ (u,A)$
is in X and satisfies (1.4), and if A is in the Coulomb gauge (1.5), then
![]() $ (u,A)\in {\mathcal C}^{\infty }({{\Omega }},\mathbb {C})\times {\mathcal C}^{\infty }({{\Omega }},\mathbb {R}^2)$
, the bound
$ (u,A)\in {\mathcal C}^{\infty }({{\Omega }},\mathbb {C})\times {\mathcal C}^{\infty }({{\Omega }},\mathbb {R}^2)$
, the bound
![]() $|u|\leq 1$
holds, and h is in
$|u|\leq 1$
holds, and h is in
![]() $H^1({{\Omega }})$
; see [Reference Sandier and Serfaty32, Proposition 3.8, 3.9, 3.10]. Thus, we can replace the fourth equation in (1.4) by
$H^1({{\Omega }})$
; see [Reference Sandier and Serfaty32, Proposition 3.8, 3.9, 3.10]. Thus, we can replace the fourth equation in (1.4) by
and we can replace the term
![]() $\int _{\mathbb {R}^2} |\mathrm {curl\,} A-h_{\operatorname {\mathrm {\text {ex}}}}|^2$
by
$\int _{\mathbb {R}^2} |\mathrm {curl\,} A-h_{\operatorname {\mathrm {\text {ex}}}}|^2$
by
![]() $\int _{{\Omega }} |\mathrm {curl\,} A-h_{\operatorname {\mathrm {\text {ex}}}}|^2$
if we consider solutions to (1.4).
$\int _{{\Omega }} |\mathrm {curl\,} A-h_{\operatorname {\mathrm {\text {ex}}}}|^2$
if we consider solutions to (1.4).
The behavior of a family of minimizers
![]() $ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
of
$ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
of
![]() $\mathrm {GL}_{\varepsilon }$
in X in the regime
$\mathrm {GL}_{\varepsilon }$
in X in the regime
![]() ${\varepsilon }\rightarrow 0$
and
${\varepsilon }\rightarrow 0$
and
![]() $\frac {h_{\operatorname {\mathrm {\text {ex}}}}}{|\log {\varepsilon }|}\rightarrow \lambda>0$
has been previously studied in [Reference Sandier and Serfaty29, Reference Sandier and Serfaty32]. The asymptotics of families of general solutions of (1.4) have also been investigated and can be found in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32]. In this article, we are interested in the behavior of stable critical points of
$\frac {h_{\operatorname {\mathrm {\text {ex}}}}}{|\log {\varepsilon }|}\rightarrow \lambda>0$
has been previously studied in [Reference Sandier and Serfaty29, Reference Sandier and Serfaty32]. The asymptotics of families of general solutions of (1.4) have also been investigated and can be found in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32]. In this article, we are interested in the behavior of stable critical points of
![]() $\mathrm {GL}_{\varepsilon }$
in X. Here,
$\mathrm {GL}_{\varepsilon }$
in X. Here,
![]() $ (u,A)$
is a stable critical point of
$ (u,A)$
is a stable critical point of
![]() $\mathrm {GL}_{\varepsilon }$
in X if
$\mathrm {GL}_{\varepsilon }$
in X if
![]() $(u,A)$
satisfies (1.4) and
$(u,A)$
satisfies (1.4) and
 $$ \begin{align} \mathrm{d}^2 \mathrm{GL}_{\varepsilon}(u,A,v,B)&:= \frac{\mathrm{d} ^2}{\mathrm{d} t^2}\Big|_{t=0}\mathrm{GL}_{\varepsilon}(u+tv,A+tB)\geq 0,\notag \\& \quad \text{ for all }(v,B)\in {\mathcal C}^{\infty}(\overline{{{\Omega}}},\mathbb{C})\times {\mathcal C}^{\infty}_c(\mathbb{R}^2,\mathbb{R}^2). \end{align} $$
$$ \begin{align} \mathrm{d}^2 \mathrm{GL}_{\varepsilon}(u,A,v,B)&:= \frac{\mathrm{d} ^2}{\mathrm{d} t^2}\Big|_{t=0}\mathrm{GL}_{\varepsilon}(u+tv,A+tB)\geq 0,\notag \\& \quad \text{ for all }(v,B)\in {\mathcal C}^{\infty}(\overline{{{\Omega}}},\mathbb{C})\times {\mathcal C}^{\infty}_c(\mathbb{R}^2,\mathbb{R}^2). \end{align} $$
Our aim is to understand if this stability property produces extra conditions in the limit
![]() ${\varepsilon } \to 0$
compared to general critical points. Note that local minimizers are stable and thus enter the framework of our study. This question was listed as an open problem (Open problem 15) in [Reference Sandier and Serfaty32]. Before stating our results, we recall briefly some results on global minimizers and general critical points. For
${\varepsilon } \to 0$
compared to general critical points. Note that local minimizers are stable and thus enter the framework of our study. This question was listed as an open problem (Open problem 15) in [Reference Sandier and Serfaty32]. Before stating our results, we recall briefly some results on global minimizers and general critical points. For
![]() $ (u_{\varepsilon },A_{\varepsilon })\in X$
, we set
$ (u_{\varepsilon },A_{\varepsilon })\in X$
, we set
Theorem 1.1 [Reference Sandier and Serfaty32, Theorem 7.2]
Let
![]() $ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of minimizers of
$ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of minimizers of
![]() $\mathrm {GL}_{\varepsilon }$
in X. Assume that
$\mathrm {GL}_{\varepsilon }$
in X. Assume that
![]() $h_{\operatorname {\mathrm {\text {ex}}}}/|\log {\varepsilon }| \rightarrow \lambda $
as
$h_{\operatorname {\mathrm {\text {ex}}}}/|\log {\varepsilon }| \rightarrow \lambda $
as
![]() ${\varepsilon } \rightarrow 0$
with
${\varepsilon } \rightarrow 0$
with
![]() $0<\lambda <+\infty $
. Then
$0<\lambda <+\infty $
. Then
with
![]() $h_*$
the unique minimizer in
$h_*$
the unique minimizer in
![]() $\{f\in H^1_1({{\Omega }})=\{f\in H^1({{\Omega }}); \mathrm {tr}_{| \partial {{\Omega }}} f=1\}; \Delta f\in \mathcal {M}({{\Omega }})\}$
of
$\{f\in H^1_1({{\Omega }})=\{f\in H^1({{\Omega }}); \mathrm {tr}_{| \partial {{\Omega }}} f=1\}; \Delta f\in \mathcal {M}({{\Omega }})\}$
of
and the solution of the obstacle problem
 $$ \begin{align*} \left\{\begin{array}{@{}rcll} h_*\in H^1_1({{\Omega}}), \quad h_*\geq 1-\frac{\lambda}{2} \text{ in } {{\Omega}} \\ \forall v\in H^1_1({{\Omega}}) \text{ such that } v \geq 1-\frac{\lambda}{2}, \quad \int_{{\Omega}} (-\Delta h_*+h_*)(v-h_*)\geq 0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{@{}rcll} h_*\in H^1_1({{\Omega}}), \quad h_*\geq 1-\frac{\lambda}{2} \text{ in } {{\Omega}} \\ \forall v\in H^1_1({{\Omega}}) \text{ such that } v \geq 1-\frac{\lambda}{2}, \quad \int_{{\Omega}} (-\Delta h_*+h_*)(v-h_*)\geq 0. \end{array} \right. \end{align*} $$
Furthermore,
 $$ \begin{align*} \lim_{{\varepsilon}\to 0} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2}=E^\lambda(h_*)=\frac{|\mu_*|({{\Omega}})}{2\lambda}+\frac12 \int_{{\Omega}} \left(|\nabla h_*|^2+|h_*-1|^2\right). \end{align*} $$
$$ \begin{align*} \lim_{{\varepsilon}\to 0} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2}=E^\lambda(h_*)=\frac{|\mu_*|({{\Omega}})}{2\lambda}+\frac12 \int_{{\Omega}} \left(|\nabla h_*|^2+|h_*-1|^2\right). \end{align*} $$
This result on minimizers is actually obtained through a
![]() $\Gamma $
-convergence result; see [Reference Sandier and Serfaty32, Chapter 7]. Note that the
$\Gamma $
-convergence result; see [Reference Sandier and Serfaty32, Chapter 7]. Note that the
![]() $\Gamma $
-limit is convex and the limiting magnetic field
$\Gamma $
-limit is convex and the limiting magnetic field
![]() $h_*$
and the limiting vorticity measure
$h_*$
and the limiting vorticity measure
![]() $\mu _*$
are uniquely characterized. In particular, whereas global minimizers of
$\mu _*$
are uniquely characterized. In particular, whereas global minimizers of
![]() $\mathrm {GL}_{\varepsilon }$
may not be unique, their vortices behave in the same way in the mean-field limit. We now turn our attention to critical points of
$\mathrm {GL}_{\varepsilon }$
may not be unique, their vortices behave in the same way in the mean-field limit. We now turn our attention to critical points of
![]() $\mathrm {GL}_{\varepsilon }$
. We make two assumptions which were used in [Reference Sandier and Serfaty31] and then relaxed in [Reference Sandier and Serfaty32, Chapter 13]. In all this article, unless stated otherwise, we assume that
$\mathrm {GL}_{\varepsilon }$
. We make two assumptions which were used in [Reference Sandier and Serfaty31] and then relaxed in [Reference Sandier and Serfaty32, Chapter 13]. In all this article, unless stated otherwise, we assume that
![]() $ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
is a family in X which satisfies
$ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
is a family in X which satisfies
where C denotes a constant which is independent of
![]() ${\varepsilon }$
. We can then state the following.
${\varepsilon }$
. We can then state the following.
Theorem 1.2 ([Reference Sandier and Serfaty31, Theorem 1], [Reference Sandier and Serfaty32, Theorem 1.7 and 13.1])
Let
![]() $\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of points in X which solve (1.4) with
$\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of points in X which solve (1.4) with
![]() $A_{\varepsilon }$
in the Coulomb gauge (1.5) and such that (1.8)-(1.9) hold. Then, up to extraction of a subsequence,
$A_{\varepsilon }$
in the Coulomb gauge (1.5) and such that (1.8)-(1.9) hold. Then, up to extraction of a subsequence,
and
Here, the divergence of a matrix is a vector whose components are obtained as the divergence of the rows of the matrix. It can be shown – see, for example, [Reference Sandier and Serfaty32, Theorem 13.1] – that with the notation of the previous theorem,
![]() $\mu (u_{\varepsilon },A_{\varepsilon })$
is close to a measure of the form
$\mu (u_{\varepsilon },A_{\varepsilon })$
is close to a measure of the form
![]() $2\pi \sum _{i=1}^{M_{\varepsilon }} d_i^{\varepsilon } \delta _{a_i^{\varepsilon }}$
, where
$2\pi \sum _{i=1}^{M_{\varepsilon }} d_i^{\varepsilon } \delta _{a_i^{\varepsilon }}$
, where
![]() $M_{\varepsilon }\in \mathbb {N}$
,
$M_{\varepsilon }\in \mathbb {N}$
,
![]() $a_i^{\varepsilon }$
can be thought of as the center of the vortices of
$a_i^{\varepsilon }$
can be thought of as the center of the vortices of
![]() $u_{\varepsilon }$
and
$u_{\varepsilon }$
and
![]() $d_i^{\varepsilon }\in \mathbb {Z}$
as their degrees. As noted in [Reference Sandier and Serfaty31], Theorem 1.2 is interesting mainly for solutions such that
$d_i^{\varepsilon }\in \mathbb {Z}$
as their degrees. As noted in [Reference Sandier and Serfaty31], Theorem 1.2 is interesting mainly for solutions such that
 $$ \begin{align} N_{\varepsilon}:=\sum_{i=1}^{M_{\varepsilon}} |d_i^{\varepsilon}| \end{align} $$
$$ \begin{align} N_{\varepsilon}:=\sum_{i=1}^{M_{\varepsilon}} |d_i^{\varepsilon}| \end{align} $$
is of same order as
![]() $h_{\operatorname {\mathrm {\text {ex}}}}$
. If this is not the case, then we should look at the limit of
$h_{\operatorname {\mathrm {\text {ex}}}}$
. If this is not the case, then we should look at the limit of
![]() $\mu (u_{\varepsilon },A_{\varepsilon })/N_{\varepsilon }$
instead, but we do not consider this case in this paper. The matrix (or the tensor)
$\mu (u_{\varepsilon },A_{\varepsilon })/N_{\varepsilon }$
instead, but we do not consider this case in this paper. The matrix (or the tensor)
![]() $T_h$
is called the stress-energy tensor associated to the energy
$T_h$
is called the stress-energy tensor associated to the energy
![]() $\mathcal {L}(h)=\frac 12 \int _{{\Omega }} (|\nabla h|^2+h^2)$
. Equation (1.10) means that h is a stationary point for
$\mathcal {L}(h)=\frac 12 \int _{{\Omega }} (|\nabla h|^2+h^2)$
. Equation (1.10) means that h is a stationary point for
![]() $\mathcal {L}$
; that is, that for any vector field
$\mathcal {L}$
; that is, that for any vector field
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
This condition on h can also be viewed as a criticality condition on the limiting vorticityFootnote
1
uniquely determining h via
![]() $\mu =-\Delta h+h$
in
$\mu =-\Delta h+h$
in
![]() ${{\Omega }}$
and
${{\Omega }}$
and
![]() $h=1$
on
$h=1$
on
![]() $\partial {{\Omega }}$
. It is obtained by passing to the limit in the first inner variations (variations of the form (1.12)) of the energy
$\partial {{\Omega }}$
. It is obtained by passing to the limit in the first inner variations (variations of the form (1.12)) of the energy
![]() $\mathrm {GL}_{\varepsilon }$
. Although for global minimizers the limiting vorticity
$\mathrm {GL}_{\varepsilon }$
. Although for global minimizers the limiting vorticity
![]() $\mu _*$
is absolutely continuous with respect to the Lebesgue measure, the criticality condition (1.10) allows for more singular measures such as measures supported on curves. It was later shown by Aydi in [Reference Aydi5] that some solutions of the GL equations (1.4) satisfying the bounds (1.8)-(1.9) have their vorticity measures that concentrate on lines or on circles.Footnote
2
The implications of the condition (1.10) on the regularity of h and
$\mu _*$
is absolutely continuous with respect to the Lebesgue measure, the criticality condition (1.10) allows for more singular measures such as measures supported on curves. It was later shown by Aydi in [Reference Aydi5] that some solutions of the GL equations (1.4) satisfying the bounds (1.8)-(1.9) have their vorticity measures that concentrate on lines or on circles.Footnote
2
The implications of the condition (1.10) on the regularity of h and
![]() $\mu $
were investigated in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32, Reference Le21, Reference Rodiac27]. In particular, it was obtained in [Reference Rodiac27] that if
$\mu $
were investigated in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32, Reference Le21, Reference Rodiac27]. In particular, it was obtained in [Reference Rodiac27] that if
![]() $h,\mu $
are as in Theorem 1.2, then the absolutely continuous part of
$h,\mu $
are as in Theorem 1.2, then the absolutely continuous part of
![]() $\mu $
is equal to
$\mu $
is equal to
![]() $h\textbf {1}_{\{|\nabla h|=0\}}$
(
$h\textbf {1}_{\{|\nabla h|=0\}}$
(
![]() $|\nabla h|$
was shown to be a continuous function in [Reference Sandier and Serfaty32, Theorem 13.1]), and the orthogonal part is supported by a locally
$|\nabla h|$
was shown to be a continuous function in [Reference Sandier and Serfaty32, Theorem 13.1]), and the orthogonal part is supported by a locally
![]() $\mathcal {H}^1$
rectifiable set. Roughly speaking, it says that
$\mathcal {H}^1$
rectifiable set. Roughly speaking, it says that
![]() $\mu $
can be supported only by sets of nonzero Lebesgue measure or by some curves.
$\mu $
can be supported only by sets of nonzero Lebesgue measure or by some curves.
1.2 Main results
In this article, we investigate the following problem: does a stability condition on a family of critical points
![]() $ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
of
$ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
of
![]() $\mathrm {GL}_{\varepsilon }$
in X imply more regularity on their limiting vorticity measures? In particular, can a family of stable solutions of (1.4) have a limiting vorticity which concentrates on curves? To answer this question, our strategy is to pass to the limit in the second inner variation of the GL energy and deduce a supplementary condition for limiting vorticity measures of stable solutions of (1.4). Then we examine if this supplementary condition implies more regularity on
$\mathrm {GL}_{\varepsilon }$
in X imply more regularity on their limiting vorticity measures? In particular, can a family of stable solutions of (1.4) have a limiting vorticity which concentrates on curves? To answer this question, our strategy is to pass to the limit in the second inner variation of the GL energy and deduce a supplementary condition for limiting vorticity measures of stable solutions of (1.4). Then we examine if this supplementary condition implies more regularity on
![]() $\mu $
.
$\mu $
.
We first explain more precisely what we mean by first and second inner variations. Let
![]() $\eta \in {\mathcal C}_c^{\infty }({{\Omega }},\mathbb {R}^2)$
; we consider its associated flow map
$\eta \in {\mathcal C}_c^{\infty }({{\Omega }},\mathbb {R}^2)$
; we consider its associated flow map
![]() $\Phi :\mathbb {R}\times {{\Omega }} \rightarrow \mathbb {R}^2$
which satisfied that for every
$\Phi :\mathbb {R}\times {{\Omega }} \rightarrow \mathbb {R}^2$
which satisfied that for every
![]() $x\in \mathbb {R}^2$
, the map
$x\in \mathbb {R}^2$
, the map
![]() $t\mapsto \Phi (t,x)$
is the unique solution to
$t\mapsto \Phi (t,x)$
is the unique solution to
 $$ \begin{align} \left\{ \begin{array}{@{}r@{\ }c@{\ }ll} \frac{\partial }{\partial t}\Phi(t,x)&=&\eta (\Phi(t,x)) \\ \Phi(0,x)&=&x. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{@{}r@{\ }c@{\ }ll} \frac{\partial }{\partial t}\Phi(t,x)&=&\eta (\Phi(t,x)) \\ \Phi(0,x)&=&x. \end{array} \right. \end{align} $$
It can be seen thanks to the Cauchy-Lipschitz theory that the flow map is well defined in
![]() $\mathbb {R} \times {{\Omega }}$
and that it is in
$\mathbb {R} \times {{\Omega }}$
and that it is in
![]() ${\mathcal C}^{\infty }(\mathbb {R}\times {{\Omega }})$
. The family
${\mathcal C}^{\infty }(\mathbb {R}\times {{\Omega }})$
. The family
![]() $\{\Phi _t\}_{t\in \mathbb {R}}$
with
$\{\Phi _t\}_{t\in \mathbb {R}}$
with
![]() $\Phi _t(\cdot )=\Phi (t,\cdot )$
is a one-parameter group of
$\Phi _t(\cdot )=\Phi (t,\cdot )$
is a one-parameter group of
![]() ${\mathcal C}^{\infty }$
-diffeomorphisms of
${\mathcal C}^{\infty }$
-diffeomorphisms of
![]() ${{\Omega }}$
with
${{\Omega }}$
with
![]() $\Phi _0=\mathrm {Id}$
. The first and second inner variations of
$\Phi _0=\mathrm {Id}$
. The first and second inner variations of
![]() $\mathrm {GL}_{\varepsilon }$
at
$\mathrm {GL}_{\varepsilon }$
at
![]() $ (u,A)$
in the direction
$ (u,A)$
in the direction
![]() $\eta $
are defined by
$\eta $
are defined by
Here, we have denoted by
![]() $ (\Phi _t^{-1})^* A$
the pullback of A, viewed as a 1-form, by the diffeomorphism
$ (\Phi _t^{-1})^* A$
the pullback of A, viewed as a 1-form, by the diffeomorphism
![]() $\Phi _t^{-1}$
. The reason for taking the pullback
$\Phi _t^{-1}$
. The reason for taking the pullback
![]() $ (\Phi _t^{-1})^* A$
and not only
$ (\Phi _t^{-1})^* A$
and not only
![]() $A\circ \Phi _t^{-1}$
is that we need to respect the gauge invariance. This will be explained in details in Section 2. Note that when working with differential forms, it is customary to take inner variations as pullbacks by
$A\circ \Phi _t^{-1}$
is that we need to respect the gauge invariance. This will be explained in details in Section 2. Note that when working with differential forms, it is customary to take inner variations as pullbacks by
![]() $\Phi _t^{-1}$
; see, for example, [Reference Serre37]. We will also see that (1.14) and (1.15) are well defined and give their expressions in Section 2. In this paper, we do not consider inner variations up to the boundary. This is because we are mainly interested in the regularity of the vorticity measures
$\Phi _t^{-1}$
; see, for example, [Reference Serre37]. We will also see that (1.14) and (1.15) are well defined and give their expressions in Section 2. In this paper, we do not consider inner variations up to the boundary. This is because we are mainly interested in the regularity of the vorticity measures
![]() $\mu $
in the interior. For the use of inner variations up to the boundary in different contexts, we refer, for example, to [Reference Le and Sternberg24, Reference Babdjian, Millot and Rodiac6].
$\mu $
in the interior. For the use of inner variations up to the boundary in different contexts, we refer, for example, to [Reference Le and Sternberg24, Reference Babdjian, Millot and Rodiac6].
Our main result is the following.
Theorem 1.3 Let
![]() $\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of points in X which solve (1.4) with
$\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of points in X which solve (1.4) with
![]() $A_{\varepsilon }$
in the Coulomb gauge (1.5) and such that (1.8)-(1.9) hold. Let h be the weak
$A_{\varepsilon }$
in the Coulomb gauge (1.5) and such that (1.8)-(1.9) hold. Let h be the weak
![]() $H^1$
-limit of
$H^1$
-limit of
![]() $h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
and
$h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
and
![]() $\mu $
be the limit in the sense of measure of
$\mu $
be the limit in the sense of measure of
![]() $\mu (u_{\varepsilon },A_{\varepsilon })/h_{\operatorname {\mathrm {\text {ex}}}}$
given in Theorem 1.2. If we assume that
$\mu (u_{\varepsilon },A_{\varepsilon })/h_{\operatorname {\mathrm {\text {ex}}}}$
given in Theorem 1.2. If we assume that
 $$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2}= \frac{|\mu|({{\Omega}})}{2\lambda } +\frac12 \int_{{\Omega}} \left(|\nabla h|^2+|h-1|^2 \right), \end{align} $$
$$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2}= \frac{|\mu|({{\Omega}})}{2\lambda } +\frac12 \int_{{\Omega}} \left(|\nabla h|^2+|h-1|^2 \right), \end{align} $$
then either
![]() $h\equiv 1$
, or for all
$h\equiv 1$
, or for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, we have
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, we have
 $$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2}&= \int_{{\Omega}} \bigg( |\mathrm{D} \eta^T \nabla^{\perp} h|^2-|\nabla h|^2 \det \mathrm{D} \eta+ h^2 [(\mathrm{div} \eta)^2-\det \mathrm{D} \eta]\bigg)\notag \\& \quad +\frac{1}{\lambda}\int_{{\Omega}} \left( \frac{|\mathrm{D} \eta|^2}{2}-\det \mathrm{D} \eta \right) \mathrm{d} |\mu|=:Q_h(\eta). \end{align} $$
$$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2}&= \int_{{\Omega}} \bigg( |\mathrm{D} \eta^T \nabla^{\perp} h|^2-|\nabla h|^2 \det \mathrm{D} \eta+ h^2 [(\mathrm{div} \eta)^2-\det \mathrm{D} \eta]\bigg)\notag \\& \quad +\frac{1}{\lambda}\int_{{\Omega}} \left( \frac{|\mathrm{D} \eta|^2}{2}-\det \mathrm{D} \eta \right) \mathrm{d} |\mu|=:Q_h(\eta). \end{align} $$
If in addition we assume that
![]() $\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
is a family of stable critical points of
$\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
is a family of stable critical points of
![]() $\mathrm {GL}_{\varepsilon }$
in X, then h satisfies
$\mathrm {GL}_{\varepsilon }$
in X, then h satisfies
It was asked in [Reference Sandier and Serfaty32, Open problem 15] if extra conditions such as (1.7) yield more regularity on the limiting vorticity measure
![]() $\mu $
. We have found that the stability condition (1.7) implies (1.17) in the limit. However, we will also see in Proposition 4.1 that a vorticity measure concentrated on a line can satisfy this former property. Since (1.17) is obtained by passing to the limit in the second inner variations, this seems to indicate that stability for inner variations alone is not sufficient to imply regularity (absolute continuity with respect to the Lebesgue measure) on the limiting vorticity measure. Inner variations are usually the variations used to deal with singularities in variational models. However, it still might be possible that, using stability for outer variations genuinely different from inner variations (i.e., not of the form
$\mu $
. We have found that the stability condition (1.7) implies (1.17) in the limit. However, we will also see in Proposition 4.1 that a vorticity measure concentrated on a line can satisfy this former property. Since (1.17) is obtained by passing to the limit in the second inner variations, this seems to indicate that stability for inner variations alone is not sufficient to imply regularity (absolute continuity with respect to the Lebesgue measure) on the limiting vorticity measure. Inner variations are usually the variations used to deal with singularities in variational models. However, it still might be possible that, using stability for outer variations genuinely different from inner variations (i.e., not of the form
![]() $(\mathrm {D} u_{\varepsilon }.\eta , -\mathrm {D} A_{\varepsilon }.\eta +\mathrm {D} \eta ^T.A_{\varepsilon })$
), one could obtain further regularity for the limiting vorticity measure.
$(\mathrm {D} u_{\varepsilon }.\eta , -\mathrm {D} A_{\varepsilon }.\eta +\mathrm {D} \eta ^T.A_{\varepsilon })$
), one could obtain further regularity for the limiting vorticity measure.
We now comment on our assumptions (1.8), (1.9), and (H). Assumption (1.8) is quite natural and is satisfied by solutions constructed in [Reference Aydi5, Reference Sandier and Serfaty32, Reference Contreras and Serfaty11, Reference Contreras and Jerrard10]. Assumption (1.9) was used in [Reference Sandier and Serfaty31] in order to have that
where
![]() $N_{\varepsilon }$
is defined in (1.11). Stable solutions of the GL equations (1.4) with an exterior magnetic field much larger than
$N_{\varepsilon }$
is defined in (1.11). Stable solutions of the GL equations (1.4) with an exterior magnetic field much larger than
![]() $|\log {\varepsilon }|$
were constructed in [Reference Sandier and Serfaty32, Reference Contreras and Serfaty11, Reference Contreras and Jerrard10], and to this respect, our assumption may appear restrictive. However, (1.9) is satisfied in [Reference Aydi5] where solutions concentrating on lines were built. Hence, singular measures can appear in the limit for this intensity of applied magnetic field, and since our purpose is to study if the stability condition implies some regularity on limiting vorticity measures, it seems natural to consider first this case. We also refer to [Reference Serfaty33, Reference Serfaty34, Reference Serfaty35] and references therein for more results on stable solutions to (1.4). Our main assumption (H) is satisfied by some solutions constructed in [Reference Aydi5]; see Corollary 4.1 and Lemma 4.1 in [Reference Aydi5]. A similar assumption of convergence of energies was used in [Reference Le22, Reference Le23, Reference Le and Sternberg24] to pass to the limit in the second inner variations for the Allen-Cahn problem and also for the nonmagnetic GL problem in dimension bigger than 3 and in a regime where the energy is bounded by
$|\log {\varepsilon }|$
were constructed in [Reference Sandier and Serfaty32, Reference Contreras and Serfaty11, Reference Contreras and Jerrard10], and to this respect, our assumption may appear restrictive. However, (1.9) is satisfied in [Reference Aydi5] where solutions concentrating on lines were built. Hence, singular measures can appear in the limit for this intensity of applied magnetic field, and since our purpose is to study if the stability condition implies some regularity on limiting vorticity measures, it seems natural to consider first this case. We also refer to [Reference Serfaty33, Reference Serfaty34, Reference Serfaty35] and references therein for more results on stable solutions to (1.4). Our main assumption (H) is satisfied by some solutions constructed in [Reference Aydi5]; see Corollary 4.1 and Lemma 4.1 in [Reference Aydi5]. A similar assumption of convergence of energies was used in [Reference Le22, Reference Le23, Reference Le and Sternberg24] to pass to the limit in the second inner variations for the Allen-Cahn problem and also for the nonmagnetic GL problem in dimension bigger than 3 and in a regime where the energy is bounded by
![]() $C|\log {\varepsilon }|$
. However, the argument we use is quite different from the ones in the above-mentioned articles which rest upon the use of Reshetnyak’s Theorem for the Allen-Cahn part or on the constancy Theorem for varifolds for the GL part. We note that passing to the limit in the second inner variations for these problems was later shown to be possible without the assumption of convergence of energies in [Reference Gaspar16] and [Reference Cheng9].
$C|\log {\varepsilon }|$
. However, the argument we use is quite different from the ones in the above-mentioned articles which rest upon the use of Reshetnyak’s Theorem for the Allen-Cahn part or on the constancy Theorem for varifolds for the GL part. We note that passing to the limit in the second inner variations for these problems was later shown to be possible without the assumption of convergence of energies in [Reference Gaspar16] and [Reference Cheng9].
1.3 The Ginzburg-Landau equations without magnetic field
We also consider the GL energy without magnetic field
and the associated Euler-Lagrange equation
With a fixed boundary condition
![]() $g \in {\mathcal C}^1(\partial {{\Omega }},\mathbb {S}^1)$
, this problem has been studied by Bethuel-Brezis-Hélein in [Reference Bethuel, Brezis and Hélein7]. The asymptotic behavior of
$g \in {\mathcal C}^1(\partial {{\Omega }},\mathbb {S}^1)$
, this problem has been studied by Bethuel-Brezis-Hélein in [Reference Bethuel, Brezis and Hélein7]. The asymptotic behavior of
![]() $\{u_{\varepsilon }\}_{{\varepsilon }>0}$
, solutions to (1.20), depends on the topological degree of g. For a nonzero degree of g, it has been proved in [Reference Bethuel, Brezis and Hélein7] that
$\{u_{\varepsilon }\}_{{\varepsilon }>0}$
, solutions to (1.20), depends on the topological degree of g. For a nonzero degree of g, it has been proved in [Reference Bethuel, Brezis and Hélein7] that
![]() $ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
converges to some limiting harmonic map with a finite number of singularities (vortices). Besides, vortices of minimizers converge to minimizers of a renormalized energy, vortices of critical points converge to critical points of this renormalized energy, and the stability also passes to the limit as shown in [Reference Serfaty36]. Here, we do not prescribe any boundary condition, and we allow the number of vortices to diverge; however, as in the case with magnetic field, we consider only a family of solutions satisfying the following bound:
$ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
converges to some limiting harmonic map with a finite number of singularities (vortices). Besides, vortices of minimizers converge to minimizers of a renormalized energy, vortices of critical points converge to critical points of this renormalized energy, and the stability also passes to the limit as shown in [Reference Serfaty36]. Here, we do not prescribe any boundary condition, and we allow the number of vortices to diverge; however, as in the case with magnetic field, we consider only a family of solutions satisfying the following bound:
A way to understand the limit as
![]() ${\varepsilon }\to 0$
of solutions
${\varepsilon }\to 0$
of solutions
![]() $u_{\varepsilon }$
to (1.20) is to look at their phases and at their Jacobian determinants. More precisely, since
$u_{\varepsilon }$
to (1.20) is to look at their phases and at their Jacobian determinants. More precisely, since
![]() ${{\Omega }}$
is simply connected and since
${{\Omega }}$
is simply connected and since
![]() $\mathrm {div} \langle iu_{\varepsilon },\nabla u_{\varepsilon } \rangle =0$
in
$\mathrm {div} \langle iu_{\varepsilon },\nabla u_{\varepsilon } \rangle =0$
in
![]() ${{\Omega }}$
, then, by using Poincaré’s lemma, we can find
${{\Omega }}$
, then, by using Poincaré’s lemma, we can find
![]() $U_{\varepsilon }\in H^1({{\Omega }},\mathbb {R})$
such that
$U_{\varepsilon }\in H^1({{\Omega }},\mathbb {R})$
such that
Note that
![]() $\partial _1 u_{\varepsilon } \wedge \partial _2 u_{\varepsilon }= \mathrm {curl\,} \langle iu_{\varepsilon },\nabla u_{\varepsilon } \rangle =\Delta U_{\varepsilon }$
. Hence, the Laplacian of
$\partial _1 u_{\varepsilon } \wedge \partial _2 u_{\varepsilon }= \mathrm {curl\,} \langle iu_{\varepsilon },\nabla u_{\varepsilon } \rangle =\Delta U_{\varepsilon }$
. Hence, the Laplacian of
![]() $U_{\varepsilon }$
is the Jacobian determinant of
$U_{\varepsilon }$
is the Jacobian determinant of
![]() $u_{\varepsilon }$
, and this quantity was proved to play a prominent role in [Reference Jerrard and Soner19]. We can see here the analogy between
$u_{\varepsilon }$
, and this quantity was proved to play a prominent role in [Reference Jerrard and Soner19]. We can see here the analogy between
![]() $U_{\varepsilon }$
and the magnetic field
$U_{\varepsilon }$
and the magnetic field
![]() $h_{\varepsilon }$
in the full GL model. The
$h_{\varepsilon }$
in the full GL model. The
![]() $\Gamma $
-limit of
$\Gamma $
-limit of
![]() $E_{\varepsilon }$
in the regime
$E_{\varepsilon }$
in the regime
![]() $E_{\varepsilon }(u_{\varepsilon }) \simeq |\log {\varepsilon }|^2$
has been studied in [Reference Jerrard and Soner20], where results analogous to the ones in [Reference Sandier and Serfaty29] are obtained. In particular, in that case, the
$E_{\varepsilon }(u_{\varepsilon }) \simeq |\log {\varepsilon }|^2$
has been studied in [Reference Jerrard and Soner20], where results analogous to the ones in [Reference Sandier and Serfaty29] are obtained. In particular, in that case, the
![]() $\Gamma $
-limit of
$\Gamma $
-limit of
![]() $E_{\varepsilon }/|\log {\varepsilon }|^2$
is given by
$E_{\varepsilon }/|\log {\varepsilon }|^2$
is given by
![]() $ \frac {|\mu |({{\Omega }})}{2}+\frac 12 \int _{{\Omega }} |\nabla U|^2$
, where U is the weak limit in
$ \frac {|\mu |({{\Omega }})}{2}+\frac 12 \int _{{\Omega }} |\nabla U|^2$
, where U is the weak limit in
![]() $H^1$
of
$H^1$
of
![]() $U_{\varepsilon }/|\log {\varepsilon }|$
and
$U_{\varepsilon }/|\log {\varepsilon }|$
and
![]() $\mu \in \mathcal {M}({{\Omega }})$
is the limit in the sense of measures of
$\mu \in \mathcal {M}({{\Omega }})$
is the limit in the sense of measures of
![]() $\Delta U_{\varepsilon }/|\log {\varepsilon }|$
(up to extraction). For solutions to (1.20), the following results were obtained in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32]: the limit satisfies
$\Delta U_{\varepsilon }/|\log {\varepsilon }|$
(up to extraction). For solutions to (1.20), the following results were obtained in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32]: the limit satisfies
![]() $\Delta U=\mu \in H^{-1}({{\Omega }})$
, and the stress-energy tensor
$\Delta U=\mu \in H^{-1}({{\Omega }})$
, and the stress-energy tensor
![]() $(S_U)_{ij}=2\partial _iU\partial _jU-|\nabla U|^2 \delta _{ij}$
for
$(S_U)_{ij}=2\partial _iU\partial _jU-|\nabla U|^2 \delta _{ij}$
for
![]() $1\leq i,j\leq 2$
is divergence-free in
$1\leq i,j\leq 2$
is divergence-free in
![]() ${{\Omega }}$
. A way to reformulate this property is to say that the quantity
${{\Omega }}$
. A way to reformulate this property is to say that the quantity
![]() $(\partial _xU)^2-(\partial _yU)^2-2i(\partial _xU)(\partial _yU)$
is homomorphic in
$(\partial _xU)^2-(\partial _yU)^2-2i(\partial _xU)(\partial _yU)$
is homomorphic in
![]() ${{\Omega }}$
. Using complex analysis techniques and techniques from sets of finite perimeters, it was proved in [Reference Rodiac26] that if
${{\Omega }}$
. Using complex analysis techniques and techniques from sets of finite perimeters, it was proved in [Reference Rodiac26] that if
![]() $\mu $
satisfies the previous limiting critical conditions, then
$\mu $
satisfies the previous limiting critical conditions, then
![]() $\mu $
is supported on a rectifiable set which is locally the the zero set of a harmonic function. Hence,
$\mu $
is supported on a rectifiable set which is locally the the zero set of a harmonic function. Hence,
![]() $\mu $
cannot be absolutely continuous with respect to the Lebesgue measure unless
$\mu $
cannot be absolutely continuous with respect to the Lebesgue measure unless
![]() $\mu =0$
. We consider here stable solutions of (1.20) – that is, solutions satisfying
$\mu =0$
. We consider here stable solutions of (1.20) – that is, solutions satisfying
As we did previously, we define the first and second inner variations of
![]() $E_{\varepsilon }$
with respect to a
$E_{\varepsilon }$
with respect to a
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }}, \mathbb {R}^2)$
by
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }}, \mathbb {R}^2)$
by
where
![]() $\Phi _t$
is defined in (1.13). We will prove in Section 2 that these quantities are well defined.
$\Phi _t$
is defined in (1.13). We will prove in Section 2 that these quantities are well defined.
Theorem 1.4 Let
![]() $ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
be a family of solutions to (1.20) satisfying (1.23) and
$ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
be a family of solutions to (1.20) satisfying (1.23) and
![]() $E_{\varepsilon }(u_{\varepsilon })\leq C|\log {\varepsilon }|^2$
. As shown in [Reference Sandier and Serfaty31, Theorem 3] or [Reference Sandier and Serfaty32], up to a subsequence,
$E_{\varepsilon }(u_{\varepsilon })\leq C|\log {\varepsilon }|^2$
. As shown in [Reference Sandier and Serfaty31, Theorem 3] or [Reference Sandier and Serfaty32], up to a subsequence,
![]() $U_{\varepsilon }/|\log {\varepsilon }|\rightharpoonup U$
in
$U_{\varepsilon }/|\log {\varepsilon }|\rightharpoonup U$
in
![]() $H^1({{\Omega }})$
and
$H^1({{\Omega }})$
and
![]() $\Delta U_{\varepsilon } / |\log {\varepsilon }|=\mathrm {curl}\, \langle iu_{\varepsilon },\nabla u_{\varepsilon } \rangle /|\log {\varepsilon }| \rightharpoonup \mu \in \mathcal {M}({{\Omega }})$
with
$\Delta U_{\varepsilon } / |\log {\varepsilon }|=\mathrm {curl}\, \langle iu_{\varepsilon },\nabla u_{\varepsilon } \rangle /|\log {\varepsilon }| \rightharpoonup \mu \in \mathcal {M}({{\Omega }})$
with
If we assume that
 $$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{E_{\varepsilon}(u_{\varepsilon})}{|\log {\varepsilon}|^2}= \frac{|\mu|({{\Omega}})}{2}+\frac12 \int_{{\Omega}} |\nabla U|^2 , \end{align} $$
$$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{E_{\varepsilon}(u_{\varepsilon})}{|\log {\varepsilon}|^2}= \frac{|\mu|({{\Omega}})}{2}+\frac12 \int_{{\Omega}} |\nabla U|^2 , \end{align} $$
then for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, we have
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, we have
 $$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{\delta^2 E_{\varepsilon} (u_{\varepsilon},\eta)}{|\log {\varepsilon}|^2}&=\frac12 \int_{{\Omega}} |\mathrm{D} \eta ^T\nabla^{\perp} U|^2-|\nabla U|^2 \det \mathrm{D} \eta + \int_{{\Omega}} \left(\frac{|\mathrm{D} \eta|^2}{2}-\det \mathrm{D} \eta \right) \mathrm{d} |\mu| \nonumber\\&=:\tilde{Q}_U (\eta). \end{align} $$
$$ \begin{align} \lim_{{\varepsilon} \to 0} \frac{\delta^2 E_{\varepsilon} (u_{\varepsilon},\eta)}{|\log {\varepsilon}|^2}&=\frac12 \int_{{\Omega}} |\mathrm{D} \eta ^T\nabla^{\perp} U|^2-|\nabla U|^2 \det \mathrm{D} \eta + \int_{{\Omega}} \left(\frac{|\mathrm{D} \eta|^2}{2}-\det \mathrm{D} \eta \right) \mathrm{d} |\mu| \nonumber\\&=:\tilde{Q}_U (\eta). \end{align} $$
Again, we can see that solutions to (1.20) satisfying (1.23) have the property that, in the limit,
![]() $\tilde {Q}_U(\eta )\geq 0$
for all admissible
$\tilde {Q}_U(\eta )\geq 0$
for all admissible
![]() $\eta $
. We can also ask if that condition provides more regularity on the possible limiting vorticies. Here, we obtain that stability for inner variations never implies regularity for the limiting vorticity measure. Indeed, thanks to a recent result of Iwaniec-Onninen [Reference Iwaniec and Onninen18, Theorem 1.12], we are able to prove that every measure satisfying the limiting criticality conditions (1.25) also satisfies the limiting stability condition:
$\eta $
. We can also ask if that condition provides more regularity on the possible limiting vorticies. Here, we obtain that stability for inner variations never implies regularity for the limiting vorticity measure. Indeed, thanks to a recent result of Iwaniec-Onninen [Reference Iwaniec and Onninen18, Theorem 1.12], we are able to prove that every measure satisfying the limiting criticality conditions (1.25) also satisfies the limiting stability condition:
![]() $\tilde {Q}_U(\eta )\geq 0$
for all admissible
$\tilde {Q}_U(\eta )\geq 0$
for all admissible
![]() $\eta $
; see Proposition 4.2. However, we have used only inner variations, and it still might be possible that stability for genuine outer variations could lead to further regularity. We should observe that, contrarily to the case of the GL equations with magnetic field, it is still an open problem to determine if there exist solutions to (1.20) with a diverging number of vortices such that their limiting vorticities concentrate on curves (which should be locally the zero set of some, possibly multi-valued, harmonic functions according to [Reference Rodiac26]).
$\eta $
; see Proposition 4.2. However, we have used only inner variations, and it still might be possible that stability for genuine outer variations could lead to further regularity. We should observe that, contrarily to the case of the GL equations with magnetic field, it is still an open problem to determine if there exist solutions to (1.20) with a diverging number of vortices such that their limiting vorticities concentrate on curves (which should be locally the zero set of some, possibly multi-valued, harmonic functions according to [Reference Rodiac26]).
1.4 Method of proof
For smooth critical points of energies, inner variations are strongly related to outer variations which are defined, in the case of
![]() $\mathrm {GL}_{\varepsilon }$
, for
$\mathrm {GL}_{\varepsilon }$
, for
![]() $(u,A)\in X$
and
$(u,A)\in X$
and
![]() $(v,B)\in {\mathcal C}^{\infty }(\overline {{{\Omega }}})\times {\mathcal C}^{\infty }_c(\mathbb {R}^2) $
by (1.3) and (1.7). Although outer variations are of more common use in variational problems, it has been observed that inner variations are useful to understand the limit of singularly perturbed problems such as the Allen-Cahn (AC) problem or the GL problem since these are variations which do move the singularities; see, for example, [Reference Bethuel, Brezis and Hélein7, Reference Hutchinson and Tonegawa17, Reference Lin and Rivière25, Reference Bethuel, Brezis and Orlandi8, Reference Sandier28, Reference Sandier and Serfaty31].
$(v,B)\in {\mathcal C}^{\infty }(\overline {{{\Omega }}})\times {\mathcal C}^{\infty }_c(\mathbb {R}^2) $
by (1.3) and (1.7). Although outer variations are of more common use in variational problems, it has been observed that inner variations are useful to understand the limit of singularly perturbed problems such as the Allen-Cahn (AC) problem or the GL problem since these are variations which do move the singularities; see, for example, [Reference Bethuel, Brezis and Hélein7, Reference Hutchinson and Tonegawa17, Reference Lin and Rivière25, Reference Bethuel, Brezis and Orlandi8, Reference Sandier28, Reference Sandier and Serfaty31].
More recently, some interest has grown in understanding how the stability condition passes to the limit in the above-mentioned problems. We refer, for example, to [Reference Le22, Reference Le23, Reference Le and Sternberg24, Reference Gaspar16, Reference Cheng9]. Again, it turns out that studying the second inner variations is more appropriate to understand the limiting behavior of stable solutions to the AC or GL problems. Looking at the expressions given by the first and second inner variations of GL type functionals – see Proposition 2.2 for the formulas – one can see that one of the difficulties is to pass to the limit in quadratic expressions involving derivatives of the unknown functions, whereas only weak convergence in
![]() $H^1$
of these functions is available. For example, the vanishing of the first inner variation of
$H^1$
of these functions is available. For example, the vanishing of the first inner variation of
![]() $\mathrm {GL}_{\varepsilon }$
provides
$\mathrm {GL}_{\varepsilon }$
provides
 $$ \begin{align} \mathrm{div}( T_{\varepsilon})=0 \text{ in } {{\Omega}}, \text{ with }(T_{\varepsilon})_{ij} &= \langle \partial_i^{A_{\varepsilon}} u_{\varepsilon},\partial_j^{A_{\varepsilon}}u_{\varepsilon}\rangle\nonumber\\ & \quad -\frac12\left( |\nabla_{A_{\varepsilon}}u_{\varepsilon}|^2+\frac{1}{2{\varepsilon}^2}(1-|u_{\varepsilon}|^2)^2-h_{\varepsilon}^2 \right)\delta_{ij}. \end{align} $$
$$ \begin{align} \mathrm{div}( T_{\varepsilon})=0 \text{ in } {{\Omega}}, \text{ with }(T_{\varepsilon})_{ij} &= \langle \partial_i^{A_{\varepsilon}} u_{\varepsilon},\partial_j^{A_{\varepsilon}}u_{\varepsilon}\rangle\nonumber\\ & \quad -\frac12\left( |\nabla_{A_{\varepsilon}}u_{\varepsilon}|^2+\frac{1}{2{\varepsilon}^2}(1-|u_{\varepsilon}|^2)^2-h_{\varepsilon}^2 \right)\delta_{ij}. \end{align} $$
The formula for the second inner variation is given in Proposition 2.2. Let us briefly recall how Sandier-Serfaty in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32] managed to pass to the limit in (1.27). First we can see, at least formally, that
Although
![]() $h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
converges only weakly in
$h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
converges only weakly in
![]() $H^1$
, Sandier-Serfaty succeeded in passing to the limit in the equation
$H^1$
, Sandier-Serfaty succeeded in passing to the limit in the equation
![]() $\mathrm {div}(T_{\varepsilon })=0$
by showing that the convergence of
$\mathrm {div}(T_{\varepsilon })=0$
by showing that the convergence of
![]() $h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
is actually strong in
$h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
is actually strong in
![]() $H^1$
outside a set of arbitrary small perimeter and by using the equation along with a co-area formula argument. This type of problem has the same flavor of the problem of understanding the limit of solutions to the incompressible Euler equations in 2D fluid mechanics; see [Reference DiPerna and Majda13, Reference Delort12].
$H^1$
outside a set of arbitrary small perimeter and by using the equation along with a co-area formula argument. This type of problem has the same flavor of the problem of understanding the limit of solutions to the incompressible Euler equations in 2D fluid mechanics; see [Reference DiPerna and Majda13, Reference Delort12].
To pass to the limit in the second inner variation, we cannot use the same argument since we have to pass to the limit in an inequality and not in an equality. We must then understand the limit of all the quadratic terms appearing in the formula given in Proposition 2.2. Assumption (H) allows us to show that the potential term
![]() $\frac {1}{2{\varepsilon }^2 h_{\operatorname {\mathrm {\text {ex}}}}^2}(1-|u|^2)^2$
converges strongly toward zero in
$\frac {1}{2{\varepsilon }^2 h_{\operatorname {\mathrm {\text {ex}}}}^2}(1-|u|^2)^2$
converges strongly toward zero in
![]() $L^1({{\Omega }})$
. Next, we say that
$L^1({{\Omega }})$
. Next, we say that
![]() $|\partial _1^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2\rightharpoonup |\partial _2h|^2+\nu _1, \ |\partial _2^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2\rightharpoonup |\partial _1h|^2+\nu _2$
and
$|\partial _1^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2\rightharpoonup |\partial _2h|^2+\nu _1, \ |\partial _2^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2\rightharpoonup |\partial _1h|^2+\nu _2$
and
![]() $\langle \partial _1^{A_{\varepsilon }}u_{\varepsilon },\partial _2^{A_{\varepsilon }}u_{\varepsilon }\rangle /h_{\operatorname {\mathrm {\text {ex}}}}^2\rightharpoonup -\partial _1 h,\partial _2h+\nu _3$
, where
$\langle \partial _1^{A_{\varepsilon }}u_{\varepsilon },\partial _2^{A_{\varepsilon }}u_{\varepsilon }\rangle /h_{\operatorname {\mathrm {\text {ex}}}}^2\rightharpoonup -\partial _1 h,\partial _2h+\nu _3$
, where
![]() $\nu _1,\nu _2,\nu _3$
are Radon measures in
$\nu _1,\nu _2,\nu _3$
are Radon measures in
![]() ${{\Omega }}$
and the convergence takes place in the sense of measures. We can then pass to the limit in the equation
${{\Omega }}$
and the convergence takes place in the sense of measures. We can then pass to the limit in the equation
![]() $\mathrm {div} ( T_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}^2)=0$
and use Theorem 1.2 to deduce an equation on
$\mathrm {div} ( T_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}^2)=0$
and use Theorem 1.2 to deduce an equation on
![]() $\nu _1,\nu _2,\nu _3$
in the interior
$\nu _1,\nu _2,\nu _3$
in the interior
![]() ${{\Omega }}$
. This equation actually means that
${{\Omega }}$
. This equation actually means that
![]() $\nu _1-\nu _2-i\nu _3$
is holomorphic in
$\nu _1-\nu _2-i\nu _3$
is holomorphic in
![]() ${{\Omega }}$
. We use again assumption (H), along with the description of possible limiting vorticity measures
${{\Omega }}$
. We use again assumption (H), along with the description of possible limiting vorticity measures
![]() $\mu $
obtained in [Reference Rodiac27], to obtain that
$\mu $
obtained in [Reference Rodiac27], to obtain that
![]() $\nu _1=\nu _2=\mu /2\lambda $
and
$\nu _1=\nu _2=\mu /2\lambda $
and
![]() $\nu _3=0$
on a ball contained in
$\nu _3=0$
on a ball contained in
![]() ${{\Omega }}$
if h is not constantly equal to
${{\Omega }}$
if h is not constantly equal to
![]() $1$
. Then the principle of isolated zeros gives
$1$
. Then the principle of isolated zeros gives
![]() $\nu _1=\nu _2=|\mu |/\lambda $
and
$\nu _1=\nu _2=|\mu |/\lambda $
and
![]() $\nu _3=0$
in all
$\nu _3=0$
in all
![]() ${{\Omega }}$
. Finally, we analyze the inequality obtained by passing in the limit in the second inner variation. In the case with magnetic field, we show in one example that we can have
${{\Omega }}$
. Finally, we analyze the inequality obtained by passing in the limit in the second inner variation. In the case with magnetic field, we show in one example that we can have
![]() $Q_h(\eta )\geq 0$
, where
$Q_h(\eta )\geq 0$
, where
![]() $Q_h$
is defined in (1.16), for all
$Q_h$
is defined in (1.16), for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }}, \mathbb {R}^2)$
and
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }}, \mathbb {R}^2)$
and
![]() $\mu $
supported by a line. We use similar arguments to treat the case without magnetic field to pass to the limit in the second inner variation. We then employ a result of Iwaniec-Onninen [Reference Iwaniec and Onninen18] to obtain that
$\mu $
supported by a line. We use similar arguments to treat the case without magnetic field to pass to the limit in the second inner variation. We then employ a result of Iwaniec-Onninen [Reference Iwaniec and Onninen18] to obtain that
![]() $\tilde {Q}_U(\eta )\geq 0$
for all
$\tilde {Q}_U(\eta )\geq 0$
for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, with
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, with
![]() $\tilde {Q}_U$
defined in (1.26).
$\tilde {Q}_U$
defined in (1.26).
1.5 Organization of the paper
The paper is organized as follows. In Section 2, we compute the expressions of the first and second inner variations. We also explain the link between inner and outer variations. Section 3 is dedicated to show how to pass to the limit in the second inner variation. In order to do this, we study the limit of all the quadratic terms appearing in the second inner variations of
![]() $\mathrm {GL}_{\varepsilon }$
by using an argument of defect measures and by using the limit of the first inner variation. Finally, Section 4 is devoted to analyze the limiting stability condition obtained in Theorem 1.3 and Theorem 1.4.
$\mathrm {GL}_{\varepsilon }$
by using an argument of defect measures and by using the limit of the first inner variation. Finally, Section 4 is devoted to analyze the limiting stability condition obtained in Theorem 1.3 and Theorem 1.4.
1.6 Notations
For
![]() $u,v$
two vectors in
$u,v$
two vectors in
![]() $\mathbb {R}^2$
, we denote by
$\mathbb {R}^2$
, we denote by
![]() $u\cdot v$
their inner product. When
$u\cdot v$
their inner product. When
![]() $u,v$
are identified with complex numbers, then we denote also their inner products by
$u,v$
are identified with complex numbers, then we denote also their inner products by
![]() $\langle u, v \rangle $
. If
$\langle u, v \rangle $
. If
![]() $\eta \in {\mathcal C}^{\infty }({{\Omega }},\mathbb {R}^2)$
is a smooth vector field, we use
$\eta \in {\mathcal C}^{\infty }({{\Omega }},\mathbb {R}^2)$
is a smooth vector field, we use
![]() $\mathrm {D} \eta $
to denote its differential. When we apply this differential to a vector
$\mathrm {D} \eta $
to denote its differential. When we apply this differential to a vector
![]() $x\in \mathbb {R}^2$
, we use
$x\in \mathbb {R}^2$
, we use
![]() $\mathrm {D} \eta .x$
. The second derivative of a smooth vector field
$\mathrm {D} \eta .x$
. The second derivative of a smooth vector field
![]() $\eta $
applied to two vectors
$\eta $
applied to two vectors
![]() $x,y\in \mathbb {R}^2$
is denoted by
$x,y\in \mathbb {R}^2$
is denoted by
![]() $ \mathrm {D}^2 \eta [x,y]$
. For two matrices
$ \mathrm {D}^2 \eta [x,y]$
. For two matrices
![]() $M,N \in \mathcal {M}_2(\mathbb {R})$
, we let
$M,N \in \mathcal {M}_2(\mathbb {R})$
, we let
![]() $ M:N:=\mathrm {tr} (M^TN)$
denote their inner product and
$ M:N:=\mathrm {tr} (M^TN)$
denote their inner product and
![]() $\|M\|$
the associated norm, with
$\|M\|$
the associated norm, with
![]() $M^T$
the transpose matrix of M. For two vectors
$M^T$
the transpose matrix of M. For two vectors
![]() $x,y\in \mathbb {R}^2$
, we define their tensor products to be a matrix in
$x,y\in \mathbb {R}^2$
, we define their tensor products to be a matrix in
![]() $\mathcal {M}_2(\mathbb {R})$
whose entries are given by
$\mathcal {M}_2(\mathbb {R})$
whose entries are given by
![]() $ (x \otimes y)_{ij}=x_iy_j$
. Note that we have the relation
$ (x \otimes y)_{ij}=x_iy_j$
. Note that we have the relation
![]() $M.x \cdot y=M: y\otimes x$
. For
$M.x \cdot y=M: y\otimes x$
. For
![]() $0$
and
$0$
and
![]() $1$
-forms f and A, we denote by
$1$
-forms f and A, we denote by
![]() $df$
and
$df$
and
![]() $ dA$
their exterior derivatives. For a function h regular enough. we set
$ dA$
their exterior derivatives. For a function h regular enough. we set
![]() $\nabla ^{\perp } h= (-\partial _2h,\partial _1h)^T$
. For a Radon measure
$\nabla ^{\perp } h= (-\partial _2h,\partial _1h)^T$
. For a Radon measure
![]() $\mu \in \mathcal {M}({{\Omega }})$
, we denote by
$\mu \in \mathcal {M}({{\Omega }})$
, we denote by
![]() $|\mu |({{\Omega }})$
its total variation. When we need to evaluate the energy on a subdomain
$|\mu |({{\Omega }})$
its total variation. When we need to evaluate the energy on a subdomain
![]() $V\subset {{\Omega }}$
we write
$V\subset {{\Omega }}$
we write
![]() $\mathrm {GL}_{\varepsilon }(u,A,V)$
.
$\mathrm {GL}_{\varepsilon }(u,A,V)$
.
2 Inner variations
In this section, we compute the first and second inner variations of
![]() $\mathrm {GL}_{\varepsilon }$
defined in (1.14)–(1.15), and we explain the link with the outer variations (1.3)–(1.7).
$\mathrm {GL}_{\varepsilon }$
defined in (1.14)–(1.15), and we explain the link with the outer variations (1.3)–(1.7).
2.1 Variations and gauge invariance
Since the functional
![]() $\mathrm {GL}_{\varepsilon }$
and physical quantities are gauge invariant, we should use variations for which the notion of stationarity does not depend on the gauge. That is why we have defined inner variations as
$\mathrm {GL}_{\varepsilon }$
and physical quantities are gauge invariant, we should use variations for which the notion of stationarity does not depend on the gauge. That is why we have defined inner variations as
![]() $ (u\circ \Phi _t^{-1}, (\Phi _t^{-1})^* A)$
and not simply as
$ (u\circ \Phi _t^{-1}, (\Phi _t^{-1})^* A)$
and not simply as
![]() $ (u \circ \Phi _t^{-1}, A\circ \Phi _t^{-1})$
.
$ (u \circ \Phi _t^{-1}, A\circ \Phi _t^{-1})$
.
Proposition 2.1 Let
![]() $ (u,A)$
and
$ (u,A)$
and
![]() $(\tilde {u},\tilde {A})$
be in X such that there exists
$(\tilde {u},\tilde {A})$
be in X such that there exists
![]() $f\in H^2_{\text {loc}}(\mathbb {R}^2,\mathbb {R})$
with
$f\in H^2_{\text {loc}}(\mathbb {R}^2,\mathbb {R})$
with
![]() $ \tilde {u}=ue^{if}$
and
$ \tilde {u}=ue^{if}$
and
![]() $ \tilde {A}= A+ \nabla f$
. Then for any
$ \tilde {A}= A+ \nabla f$
. Then for any
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
with
![]() $\delta \mathrm {GL}_{\varepsilon }(u,A,\eta )$
and
$\delta \mathrm {GL}_{\varepsilon }(u,A,\eta )$
and
![]() $ \delta ^2 \mathrm {GL}_{\varepsilon }(u,A,\eta )$
defined in (1.14)–(1.15).
$ \delta ^2 \mathrm {GL}_{\varepsilon }(u,A,\eta )$
defined in (1.14)–(1.15).
Proof We let
![]() $ (u_t,A_t):=(u\circ \Phi _t^{-1}, (\Phi _t^{-1})^* A)$
, where
$ (u_t,A_t):=(u\circ \Phi _t^{-1}, (\Phi _t^{-1})^* A)$
, where
![]() $\Phi _t$
is defined in (1.13). The gauge invariance implies that
$\Phi _t$
is defined in (1.13). The gauge invariance implies that
 $$ \begin{align*} \mathrm{GL}_{\varepsilon} (u_t,A_t)&=\mathrm{GL}_{\varepsilon}(u_te^{if},A_t+d f) \\&=\mathrm{GL}_{\varepsilon}(u_te^{if_t} e^{i(f-f_t)},A_t+df_t+d(f-f_t)), \end{align*} $$
$$ \begin{align*} \mathrm{GL}_{\varepsilon} (u_t,A_t)&=\mathrm{GL}_{\varepsilon}(u_te^{if},A_t+d f) \\&=\mathrm{GL}_{\varepsilon}(u_te^{if_t} e^{i(f-f_t)},A_t+df_t+d(f-f_t)), \end{align*} $$
where
![]() $f_t=f\circ \Phi _t^{-1}$
. Since
$f_t=f\circ \Phi _t^{-1}$
. Since
![]() $ \mathrm {D} f_t =\mathrm {D} f(\Phi _t^{-1}).\mathrm {D} \Phi _t^{-1}$
, we find that, as forms,
$ \mathrm {D} f_t =\mathrm {D} f(\Phi _t^{-1}).\mathrm {D} \Phi _t^{-1}$
, we find that, as forms,
![]() $df_t=(\Phi _t^{-1})^*df$
. Hence, we infer that
$df_t=(\Phi _t^{-1})^*df$
. Hence, we infer that
![]() $ A_t+df_t= (\Phi _t^{-1})^*(A+df)$
, and thus, using once again the gauge invariance,
$ A_t+df_t= (\Phi _t^{-1})^*(A+df)$
, and thus, using once again the gauge invariance,
with
![]() $(\tilde {u}_t,\tilde {A}_t)=(\tilde {u}\circ \Phi _t^{-1}, (\Phi _t^{-1})^* \tilde {A})$
. Differentiating with respect to t yields (2.1).
$(\tilde {u}_t,\tilde {A}_t)=(\tilde {u}\circ \Phi _t^{-1}, (\Phi _t^{-1})^* \tilde {A})$
. Differentiating with respect to t yields (2.1).
It can be checked by direct computation that the quantity
![]() $\frac {\mathrm {d}}{\mathrm {d} t}\Big |_{t=0} \mathrm {GL}_{\varepsilon }(u\circ \Phi _t^{-1}, A\circ \Phi _t^{-1})$
and its second-order analogue are not gauge invariant. However, we observe that outer variations are also well adapted to the gauge invariance in the sense that if
$\frac {\mathrm {d}}{\mathrm {d} t}\Big |_{t=0} \mathrm {GL}_{\varepsilon }(u\circ \Phi _t^{-1}, A\circ \Phi _t^{-1})$
and its second-order analogue are not gauge invariant. However, we observe that outer variations are also well adapted to the gauge invariance in the sense that if
![]() $(u,A)\in X$
is a critical point of
$(u,A)\in X$
is a critical point of
![]() $ \mathrm {GL}_{\varepsilon }$
. Then
$ \mathrm {GL}_{\varepsilon }$
. Then
![]() $ (ue^{if},A+df)$
is also a critical point of
$ (ue^{if},A+df)$
is also a critical point of
![]() $\mathrm {GL}_{\varepsilon }$
in X for
$\mathrm {GL}_{\varepsilon }$
in X for
![]() $f\in H^2_{\text {loc}}(\mathbb {R}^2,\mathbb {R})$
, and if
$f\in H^2_{\text {loc}}(\mathbb {R}^2,\mathbb {R})$
, and if
![]() $ (u,A)$
is stable, then so is
$ (u,A)$
is stable, then so is
![]() $(ue^{if},A+df)$
. This follows, for example, by observing that for
$(ue^{if},A+df)$
. This follows, for example, by observing that for
![]() $t\in \mathbb {R}$
and for any
$t\in \mathbb {R}$
and for any
![]() $ (v,B)\in X$
, we have
$ (v,B)\in X$
, we have
![]() $\mathrm {GL}_{\varepsilon }(u+tv,A+tB)=\mathrm {GL}_{\varepsilon } (ue^{if}+tve^{if},A+df+tB)$
. Hence differentiating with respect to t entails that
$\mathrm {GL}_{\varepsilon }(u+tv,A+tB)=\mathrm {GL}_{\varepsilon } (ue^{if}+tve^{if},A+df+tB)$
. Hence differentiating with respect to t entails that
![]() $ \mathrm {d} \mathrm {GL}_{\varepsilon }(u,A).(v,B)=\mathrm {d} \mathrm {GL}_{\varepsilon }(ue^{if}, A+df).(ve^{if},B)$
and
$ \mathrm {d} \mathrm {GL}_{\varepsilon }(u,A).(v,B)=\mathrm {d} \mathrm {GL}_{\varepsilon }(ue^{if}, A+df).(ve^{if},B)$
and
![]() $ \mathrm {d}^2\mathrm {GL}_{\varepsilon } (u,A).(v,B)=\mathrm {d}^2\mathrm {GL}_{\varepsilon }(ue^{if},A+df).(ve^{if},B)$
.
$ \mathrm {d}^2\mathrm {GL}_{\varepsilon } (u,A).(v,B)=\mathrm {d}^2\mathrm {GL}_{\varepsilon }(ue^{if},A+df).(ve^{if},B)$
.
2.2 Inner variations and outer variations for the GL energy
To compute the first and second inner and outer variations of the GL energy in the magnetic and nonmagnetic case, we first rewrite these energies by using the vectorial setting instead of the complex one. Namely, we see the order parameter as a map
![]() $u:{{\Omega }}\rightarrow \mathbb {R}^2$
, and we write
$u:{{\Omega }}\rightarrow \mathbb {R}^2$
, and we write
![]() $\mathrm {D} u\in \mathcal {M}_2(\mathbb {R})$
for its differential (instead of
$\mathrm {D} u\in \mathcal {M}_2(\mathbb {R})$
for its differential (instead of
![]() $\nabla u$
for its complex gradient). We can check that the complex covariant gradient
$\nabla u$
for its complex gradient). We can check that the complex covariant gradient
![]() $ (\nabla -iA)u$
corresponds to the real matrix
$ (\nabla -iA)u$
corresponds to the real matrix
 $\begin {pmatrix} \partial _1u_1+A_1u_2 & \partial _2u_1+A_2u_2 \\ \partial _1u_2-A_1u_1 & \partial _2u_2-A_2u_1 \end {pmatrix}$
. Thus, if we define
$\begin {pmatrix} \partial _1u_1+A_1u_2 & \partial _2u_1+A_2u_2 \\ \partial _1u_2-A_1u_1 & \partial _2u_2-A_2u_1 \end {pmatrix}$
. Thus, if we define
 $u^{\perp }:= \begin {pmatrix} -u_2 \\ u_1 \end {pmatrix}$
, we find that
$u^{\perp }:= \begin {pmatrix} -u_2 \\ u_1 \end {pmatrix}$
, we find that
![]() $ (\nabla -iA)u$
corresponds to
$ (\nabla -iA)u$
corresponds to
![]() $ \mathrm {D} u-u^{\perp } A^T$
and
$ \mathrm {D} u-u^{\perp } A^T$
and
General formulas for the first and inner variations of functionals are given in [Reference Le22, Reference Le23, Reference Le and Sternberg24]. We present the computations here because our setting is slightly different due to the presence of the magnetic field and the term
![]() $(\Phi _t^{-1})^*\circ A$
.
$(\Phi _t^{-1})^*\circ A$
.
Proposition 2.2 Let
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
![]() $\zeta :=\mathrm {D} \eta .\eta $
and
$\zeta :=\mathrm {D} \eta .\eta $
and
![]() $(u,A)\in X$
. Then, with definitions (1.14) and (1.15), we have
$(u,A)\in X$
. Then, with definitions (1.14) and (1.15), we have
 $$ \begin{align*} \delta \mathrm{GL}_{\varepsilon}(u,A,\eta )&= \int_{{\Omega}} \Big[ \frac12 \left( |\mathrm{D} u-u^{\perp} A^T|^2-h^2+\frac{1}{2{\varepsilon}^2}(1-|u|^2)^2 \right)\mathrm{Id} \\& \quad\qquad -(\mathrm{D} u-u^{\perp} A^T)^T(\mathrm{D} u-u^{\perp} A^T) \Big]: \mathrm{D} \eta \end{align*} $$
$$ \begin{align*} \delta \mathrm{GL}_{\varepsilon}(u,A,\eta )&= \int_{{\Omega}} \Big[ \frac12 \left( |\mathrm{D} u-u^{\perp} A^T|^2-h^2+\frac{1}{2{\varepsilon}^2}(1-|u|^2)^2 \right)\mathrm{Id} \\& \quad\qquad -(\mathrm{D} u-u^{\perp} A^T)^T(\mathrm{D} u-u^{\perp} A^T) \Big]: \mathrm{D} \eta \end{align*} $$
 $$ \begin{align*} \delta^2\mathrm{GL}_{\varepsilon}(u,A,\eta)&=\delta \mathrm{GL}_{\varepsilon}(u,A, \zeta) +\int_{{\Omega}} \Big[ |(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \eta|^2 -|\mathrm{D} u-u^{\perp} A^T|^2 \det \mathrm{D} \eta \\& \qquad\qquad\qquad +h^2( (\mathrm{div} \eta)^2-\det \mathrm{D} \eta) +\frac{1}{2{\varepsilon}^2}(1-|u|^2)^2\det \mathrm{D} \eta \Big]. \end{align*} $$
$$ \begin{align*} \delta^2\mathrm{GL}_{\varepsilon}(u,A,\eta)&=\delta \mathrm{GL}_{\varepsilon}(u,A, \zeta) +\int_{{\Omega}} \Big[ |(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \eta|^2 -|\mathrm{D} u-u^{\perp} A^T|^2 \det \mathrm{D} \eta \\& \qquad\qquad\qquad +h^2( (\mathrm{div} \eta)^2-\det \mathrm{D} \eta) +\frac{1}{2{\varepsilon}^2}(1-|u|^2)^2\det \mathrm{D} \eta \Big]. \end{align*} $$
Proof Let
![]() $\{\Phi _t\}_{t\in \mathbb {R}}$
be the flow associated to
$\{\Phi _t\}_{t\in \mathbb {R}}$
be the flow associated to
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
defined in (1.13), and let
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
defined in (1.13), and let
![]() $ (u_t,A_t):=(u\circ \Phi _t^{-1}, (\Phi _t^{-1})^*A)$
. By definition of the pullback,
$ (u_t,A_t):=(u\circ \Phi _t^{-1}, (\Phi _t^{-1})^*A)$
. By definition of the pullback,
 $$ \begin{align} A_t&=A_1\circ \Phi_t^{-1} d(\Phi_t^{-1})_1+A_2\circ \Phi_t^{-1} d(\Phi_t^{-1})_2 \nonumber \\ &=(A\circ \Phi_t^{-1})\cdot \partial_1 (\Phi_t^{-1}) dx_1 +(A\circ \Phi_t^{-1})\cdot \partial_2 (\Phi_t^{-1}) dx_2. \end{align} $$
$$ \begin{align} A_t&=A_1\circ \Phi_t^{-1} d(\Phi_t^{-1})_1+A_2\circ \Phi_t^{-1} d(\Phi_t^{-1})_2 \nonumber \\ &=(A\circ \Phi_t^{-1})\cdot \partial_1 (\Phi_t^{-1}) dx_1 +(A\circ \Phi_t^{-1})\cdot \partial_2 (\Phi_t^{-1}) dx_2. \end{align} $$
By identifying
![]() $A_t$
with a vector field in
$A_t$
with a vector field in
![]() $\mathbb {R}^2$
, we find that
$\mathbb {R}^2$
, we find that
![]() $A_t= \mathrm {D} \Phi _t^{-T}. (A\circ \Phi _t^{-1}) $
. Here,
$A_t= \mathrm {D} \Phi _t^{-T}. (A\circ \Phi _t^{-1}) $
. Here,
![]() $\mathrm {D} \Phi _t^{-T}$
denotes
$\mathrm {D} \Phi _t^{-T}$
denotes
![]() $(\mathrm {D} \Phi _t^{-1})^T$
. Thus,
$(\mathrm {D} \Phi _t^{-1})^T$
. Thus,
![]() $ \mathrm {D} u_t-u_t^{\perp } A_t^T= \left [(\mathrm {D} u-u^{\perp } A^T)\circ \Phi _t^{-1} \right ]\mathrm {D} \Phi _t^{-1}$
, and by using the change of variables
$ \mathrm {D} u_t-u_t^{\perp } A_t^T= \left [(\mathrm {D} u-u^{\perp } A^T)\circ \Phi _t^{-1} \right ]\mathrm {D} \Phi _t^{-1}$
, and by using the change of variables
![]() $x=\Phi _t(y)$
, we find
$x=\Phi _t(y)$
, we find
 $$ \begin{align*} \int_{{\Omega}} | \mathrm{D} u_t-u_t^{\perp} A_t^T|^2&=\int_{{\Omega}} |(\mathrm{D} u-u^{\perp} A^T)(\Phi_t^{-1}(x))\mathrm{D} \Phi_t^{-1}(x)|^2 \mathrm{d} x\\ &= \int_{{\Omega}} |(\mathrm{D} u-u^{\perp} A^T)(y) \mathrm{D} \Phi_t^{-1}(\Phi_t(y))|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y \\ &=\int_{{\Omega}} |(\mathrm{D} u-u^{\perp} A^T)(y) (\mathrm{D} \Phi_t(y))^{-1}|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y. \end{align*} $$
$$ \begin{align*} \int_{{\Omega}} | \mathrm{D} u_t-u_t^{\perp} A_t^T|^2&=\int_{{\Omega}} |(\mathrm{D} u-u^{\perp} A^T)(\Phi_t^{-1}(x))\mathrm{D} \Phi_t^{-1}(x)|^2 \mathrm{d} x\\ &= \int_{{\Omega}} |(\mathrm{D} u-u^{\perp} A^T)(y) \mathrm{D} \Phi_t^{-1}(\Phi_t(y))|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y \\ &=\int_{{\Omega}} |(\mathrm{D} u-u^{\perp} A^T)(y) (\mathrm{D} \Phi_t(y))^{-1}|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y. \end{align*} $$
We now look for an expansion of
![]() $(\mathrm {D} \Phi _t)^{-1}$
and
$(\mathrm {D} \Phi _t)^{-1}$
and
![]() $\det \mathrm {D} \Phi _t$
. We use the Taylor formula with integral remainder and equation (1.13) to say that
$\det \mathrm {D} \Phi _t$
. We use the Taylor formula with integral remainder and equation (1.13) to say that
 $$ \begin{align} \Phi_t(x)&=x+t\partial_t |_{t=0} \Phi_t(x)+\frac{t^2}{2} \partial^2_{tt}|_{t=0} \Phi_t(x)+O(t^3) \nonumber \\ &= x+t\eta (\Phi_t(x))+\frac{t^2}{2}\mathrm{D} \eta (x).\eta(x) +O(t^3) \end{align} $$
$$ \begin{align} \Phi_t(x)&=x+t\partial_t |_{t=0} \Phi_t(x)+\frac{t^2}{2} \partial^2_{tt}|_{t=0} \Phi_t(x)+O(t^3) \nonumber \\ &= x+t\eta (\Phi_t(x))+\frac{t^2}{2}\mathrm{D} \eta (x).\eta(x) +O(t^3) \end{align} $$
where, thanks to the compactness of the support of
![]() $\eta $
the term
$\eta $
the term
![]() $ O(t^3)$
, is such that
$ O(t^3)$
, is such that
![]() $O(t^3)/t^3$
is bounded uniformly in
$O(t^3)/t^3$
is bounded uniformly in
![]() $x\in {{\Omega }}$
. We can check that we can differentiate with respect to x under the integral sign giving the term
$x\in {{\Omega }}$
. We can check that we can differentiate with respect to x under the integral sign giving the term
![]() $O(t^3)$
to obtain that
$O(t^3)$
to obtain that
![]() $ \mathrm {D} \Phi _t= \mathrm {Id}+t \mathrm {D} \eta +\frac {t^2}{2}\mathrm {D} \zeta +O(t^3)$
with
$ \mathrm {D} \Phi _t= \mathrm {Id}+t \mathrm {D} \eta +\frac {t^2}{2}\mathrm {D} \zeta +O(t^3)$
with
![]() $\zeta = \mathrm {D} \eta .\eta $
. Now we use that for a matrix
$\zeta = \mathrm {D} \eta .\eta $
. Now we use that for a matrix
![]() $M\in \mathcal {M}_2(\mathbb {R})$
such that
$M\in \mathcal {M}_2(\mathbb {R})$
such that
![]() $\|M\|<1$
, we have
$\|M\|<1$
, we have
![]() $ (I+M)^{-1}=I-M+M^2 +O(\|M\|^3)$
to conclude that
$ (I+M)^{-1}=I-M+M^2 +O(\|M\|^3)$
to conclude that
To compute the determinant
![]() $\det \mathrm {D} \Phi _t$
, we recall that for two matrices
$\det \mathrm {D} \Phi _t$
, we recall that for two matrices
![]() $M,N$
, we have
$M,N$
, we have
 $$ \begin{align} \det \left( \mathrm{Id}+tM+\frac{t^2}{2}N\right)=1+t\mathrm{tr}(M)+\frac{t^2}{2}\left[\mathrm{tr}(N)+(\mathrm{tr}(M))^2-\mathrm{tr}(M^2)) \right] +O(t^3)\nonumber\\ \end{align} $$
$$ \begin{align} \det \left( \mathrm{Id}+tM+\frac{t^2}{2}N\right)=1+t\mathrm{tr}(M)+\frac{t^2}{2}\left[\mathrm{tr}(N)+(\mathrm{tr}(M))^2-\mathrm{tr}(M^2)) \right] +O(t^3)\nonumber\\ \end{align} $$
and that
since
 $$ \begin{align} \mathrm{D} \eta \left[(\mathrm{div} \eta)\mathrm{Id}-\mathrm{D} \eta\right]&=\begin{pmatrix} \partial_1\eta_1 &\partial_2\eta_1 \\ \partial_1\eta_2 &\partial_2\eta_2 \end{pmatrix}\begin{pmatrix} \partial_2\eta_2 &-\partial_2\eta_1 \\ -\partial_1\eta_2 &\partial_1\eta_1 \end{pmatrix} \nonumber\\ &=\begin{pmatrix} \partial_1\eta_1\partial_2\eta_2-\partial_2\eta_1\partial_1\eta_2 &0 \\ 0 &-\partial_2\eta_1\partial_1\eta_2+\partial_1\eta_1\partial_2\eta_2\end{pmatrix} \nonumber\\ &=(\det \mathrm{D} \eta) \mathrm{Id}. \end{align} $$
$$ \begin{align} \mathrm{D} \eta \left[(\mathrm{div} \eta)\mathrm{Id}-\mathrm{D} \eta\right]&=\begin{pmatrix} \partial_1\eta_1 &\partial_2\eta_1 \\ \partial_1\eta_2 &\partial_2\eta_2 \end{pmatrix}\begin{pmatrix} \partial_2\eta_2 &-\partial_2\eta_1 \\ -\partial_1\eta_2 &\partial_1\eta_1 \end{pmatrix} \nonumber\\ &=\begin{pmatrix} \partial_1\eta_1\partial_2\eta_2-\partial_2\eta_1\partial_1\eta_2 &0 \\ 0 &-\partial_2\eta_1\partial_1\eta_2+\partial_1\eta_1\partial_2\eta_2\end{pmatrix} \nonumber\\ &=(\det \mathrm{D} \eta) \mathrm{Id}. \end{align} $$
Thus,
Hence, we expand
 $$ \begin{align} \int_{{\Omega}} | \mathrm{D} u_t-u_t^{\perp} A_t^T|^2&=\int_{{\Omega}} \Bigg[\left| (\mathrm{D} u-u^{\perp} A^T)\left(\mathrm{Id}-t\mathrm{D} \eta -\frac{t^2}{2}\mathrm{D} \zeta +t^2 ( \mathrm{D} \eta)^2 +O(t^3)\right)\right|^2 \nonumber \\& \qquad\quad \times \left(1+t\mathrm{div} \eta +\frac{t^2}{2}\mathrm{div} \zeta+t^2 \det \mathrm{D} \eta +O(t^3)\right) \Bigg] \nonumber \\&= \int_{{\Omega}} \Big[ |\mathrm{D} u-u^{\perp} A^T|^2-2t (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \eta \nonumber \\& \quad\qquad + t|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \eta -t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \zeta\nonumber \\& \quad \qquad +\frac{t^2}{2}|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \zeta +t^2|(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta|^2 \nonumber \\& \quad \quad \quad +2t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) (\mathrm{D} \eta)^2 \nonumber \\&\quad \quad \quad -2t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta \mathrm{div} \eta \nonumber \\&\quad \quad \quad +t^2|\mathrm{D} u-u^{\perp} A^T|^2\det \mathrm{D} \eta +O(t^3)\Big] \nonumber \\&=\int_{{\Omega}} \Big[ |\mathrm{D} u-u^{\perp} A^T|^2-2t (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \eta \nonumber \\& \quad \qquad + t|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \eta -t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \zeta\nonumber \\& \qquad \quad +\frac{t^2}{2}|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \zeta +t^2 |(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta|^2\nonumber \\& \quad \quad \quad -|\mathrm{D} u-u^{\perp} A^T|^2\det \mathrm{D} \eta\Big] +O(t^3), \end{align} $$
$$ \begin{align} \int_{{\Omega}} | \mathrm{D} u_t-u_t^{\perp} A_t^T|^2&=\int_{{\Omega}} \Bigg[\left| (\mathrm{D} u-u^{\perp} A^T)\left(\mathrm{Id}-t\mathrm{D} \eta -\frac{t^2}{2}\mathrm{D} \zeta +t^2 ( \mathrm{D} \eta)^2 +O(t^3)\right)\right|^2 \nonumber \\& \qquad\quad \times \left(1+t\mathrm{div} \eta +\frac{t^2}{2}\mathrm{div} \zeta+t^2 \det \mathrm{D} \eta +O(t^3)\right) \Bigg] \nonumber \\&= \int_{{\Omega}} \Big[ |\mathrm{D} u-u^{\perp} A^T|^2-2t (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \eta \nonumber \\& \quad\qquad + t|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \eta -t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \zeta\nonumber \\& \quad \qquad +\frac{t^2}{2}|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \zeta +t^2|(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta|^2 \nonumber \\& \quad \quad \quad +2t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) (\mathrm{D} \eta)^2 \nonumber \\&\quad \quad \quad -2t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta \mathrm{div} \eta \nonumber \\&\quad \quad \quad +t^2|\mathrm{D} u-u^{\perp} A^T|^2\det \mathrm{D} \eta +O(t^3)\Big] \nonumber \\&=\int_{{\Omega}} \Big[ |\mathrm{D} u-u^{\perp} A^T|^2-2t (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \eta \nonumber \\& \quad \qquad + t|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \eta -t^2 (\mathrm{D} u-u^{\perp} A^T):(\mathrm{D} u-u^{\perp} A^T) \mathrm{D} \zeta\nonumber \\& \qquad \quad +\frac{t^2}{2}|\mathrm{D} u-u^{\perp} A^T|^2 \mathrm{div} \zeta +t^2 |(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta|^2\nonumber \\& \quad \quad \quad -|\mathrm{D} u-u^{\perp} A^T|^2\det \mathrm{D} \eta\Big] +O(t^3), \end{align} $$
where we have used (2.6) again. However, we know that
Hence,
 $$ \begin{align*} \int_{{\Omega}} |h_t-h_{\operatorname{\mathrm{\text{ex}}}}|^2 &=\int_{{\Omega}} |h(\Phi_t^{-1}(x))\det \mathrm{D} \Phi_t^{-1}(x)-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \mathrm{d} x\\ &=\int_{{\Omega}} |h(y)\det \mathrm{D} \Phi_t^{-1}(\Phi_t(y))-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y\\ &=\int_{{\Omega}} | h(y)\det (\mathrm{D} \Phi_t(y))^{-1}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y. \end{align*} $$
$$ \begin{align*} \int_{{\Omega}} |h_t-h_{\operatorname{\mathrm{\text{ex}}}}|^2 &=\int_{{\Omega}} |h(\Phi_t^{-1}(x))\det \mathrm{D} \Phi_t^{-1}(x)-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \mathrm{d} x\\ &=\int_{{\Omega}} |h(y)\det \mathrm{D} \Phi_t^{-1}(\Phi_t(y))-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y\\ &=\int_{{\Omega}} | h(y)\det (\mathrm{D} \Phi_t(y))^{-1}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y. \end{align*} $$
By using (2.7), we find that
 $$ \begin{align} \int_{{\Omega}} |h_t-h_{\operatorname{\mathrm{\text{ex}}}}|^2 &=\int_{{\Omega}} \left[\left|h\left(1-t\mathrm{div} \eta+\frac{t^2}{2}\mathrm{div} \zeta-t^2 \det \mathrm{D} \eta+t^2 (\mathrm{div} \eta)^2\right)-h_{\operatorname{\mathrm{\text{ex}}}}\right|^2 \right.\nonumber \\&\quad \qquad \times \left.\left(1+t\mathrm{div} \eta +\frac{t^2}{2}\mathrm{div} \zeta+t^2\det \mathrm{D} \eta\right)\right] +O(t^3) \nonumber \\&= \int_{{\Omega}} \Big[|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2 -2t(h-h_{\operatorname{\mathrm{\text{ex}}}})h \mathrm{div} \eta -t^2(h-h_{\operatorname{\mathrm{\text{ex}}}})h\mathrm{div} \zeta +t^2 h^2 (\mathrm{div} \eta)^2 \nonumber \\& \quad\qquad -2t^2 (h-h_{\operatorname{\mathrm{\text{ex}}}})h\det \mathrm{D} \eta +2t^2(h-h_{\operatorname{\mathrm{\text{ex}}}})h(\mathrm{div} \eta )^2 \nonumber \\& \qquad\quad +t|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2\mathrm{div} \eta + \frac{t^2}{2}|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2\mathrm{div} \zeta +t^2|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2\det \mathrm{D} \eta\nonumber \\& \qquad\quad -2t^2 (h-h_{\operatorname{\mathrm{\text{ex}}}})h(\mathrm{div} \eta)^2 \Big] + O(t^3) \nonumber \\&=\int_{{\Omega}}\Big[|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2-th^2\mathrm{div} \eta +th_{\operatorname{\mathrm{\text{ex}}}}^2\mathrm{div} \eta-t^2h^2\mathrm{div} \eta +t^2h_{\operatorname{\mathrm{\text{ex}}}}^2\mathrm{div} \eta\nonumber\\& \qquad\quad -t^2h^2\det \mathrm{D} \eta +h_{\operatorname{\mathrm{\text{ex}}}}^2\det \mathrm{D} \eta +t^2h^2 (\mathrm{div} \eta)^2\Big] +O(t^3) \nonumber\\&=\int_{{\Omega}} \Big[|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2-th^2\mathrm{div} \eta-t^2h^2\mathrm{div} \zeta -t^2h^2\det \mathrm{D} \eta +t^2h^2 (\mathrm{div} \eta)^2 \Big] \nonumber \\&\quad+O(t^3). \end{align} $$
$$ \begin{align} \int_{{\Omega}} |h_t-h_{\operatorname{\mathrm{\text{ex}}}}|^2 &=\int_{{\Omega}} \left[\left|h\left(1-t\mathrm{div} \eta+\frac{t^2}{2}\mathrm{div} \zeta-t^2 \det \mathrm{D} \eta+t^2 (\mathrm{div} \eta)^2\right)-h_{\operatorname{\mathrm{\text{ex}}}}\right|^2 \right.\nonumber \\&\quad \qquad \times \left.\left(1+t\mathrm{div} \eta +\frac{t^2}{2}\mathrm{div} \zeta+t^2\det \mathrm{D} \eta\right)\right] +O(t^3) \nonumber \\&= \int_{{\Omega}} \Big[|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2 -2t(h-h_{\operatorname{\mathrm{\text{ex}}}})h \mathrm{div} \eta -t^2(h-h_{\operatorname{\mathrm{\text{ex}}}})h\mathrm{div} \zeta +t^2 h^2 (\mathrm{div} \eta)^2 \nonumber \\& \quad\qquad -2t^2 (h-h_{\operatorname{\mathrm{\text{ex}}}})h\det \mathrm{D} \eta +2t^2(h-h_{\operatorname{\mathrm{\text{ex}}}})h(\mathrm{div} \eta )^2 \nonumber \\& \qquad\quad +t|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2\mathrm{div} \eta + \frac{t^2}{2}|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2\mathrm{div} \zeta +t^2|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2\det \mathrm{D} \eta\nonumber \\& \qquad\quad -2t^2 (h-h_{\operatorname{\mathrm{\text{ex}}}})h(\mathrm{div} \eta)^2 \Big] + O(t^3) \nonumber \\&=\int_{{\Omega}}\Big[|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2-th^2\mathrm{div} \eta +th_{\operatorname{\mathrm{\text{ex}}}}^2\mathrm{div} \eta-t^2h^2\mathrm{div} \eta +t^2h_{\operatorname{\mathrm{\text{ex}}}}^2\mathrm{div} \eta\nonumber\\& \qquad\quad -t^2h^2\det \mathrm{D} \eta +h_{\operatorname{\mathrm{\text{ex}}}}^2\det \mathrm{D} \eta +t^2h^2 (\mathrm{div} \eta)^2\Big] +O(t^3) \nonumber\\&=\int_{{\Omega}} \Big[|h-h_{\operatorname{\mathrm{\text{ex}}}}|^2-th^2\mathrm{div} \eta-t^2h^2\mathrm{div} \zeta -t^2h^2\det \mathrm{D} \eta +t^2h^2 (\mathrm{div} \eta)^2 \Big] \nonumber \\&\quad+O(t^3). \end{align} $$
We have used that, since
![]() $\eta $
has compact support,
$\eta $
has compact support,
![]() $\int _{{\Omega }} \mathrm {div} \eta $
and
$\int _{{\Omega }} \mathrm {div} \eta $
and
![]() $\int _{{\Omega }} \det \mathrm {D} \eta =\frac 12 \int _{{\Omega }} \mathrm {div} (\eta \wedge \partial _2 \eta , \partial _1 \eta \wedge \eta )$
vanish. At last, using again (2.7), we compute
$\int _{{\Omega }} \det \mathrm {D} \eta =\frac 12 \int _{{\Omega }} \mathrm {div} (\eta \wedge \partial _2 \eta , \partial _1 \eta \wedge \eta )$
vanish. At last, using again (2.7), we compute
 $$ \begin{align} \int_{{\Omega}} (1-|u_t|^2)^2&= \int_{{\Omega}} (1-u(\Phi_t^{-1}(x))|^2)^2 \mathrm{d} x= \int_{{\Omega}} (1-|u(y)|^2)^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y \nonumber \\ &=\int_{{\Omega}} (1-|u|^2)^2 (1+t \mathrm{div} \eta +\frac{t^2}{2}\mathrm{div} \zeta +t^2 \det \mathrm{D} \eta)+O(t^3). \end{align} $$
$$ \begin{align} \int_{{\Omega}} (1-|u_t|^2)^2&= \int_{{\Omega}} (1-u(\Phi_t^{-1}(x))|^2)^2 \mathrm{d} x= \int_{{\Omega}} (1-|u(y)|^2)^2 \det \mathrm{D} \Phi_t(y) \mathrm{d} y \nonumber \\ &=\int_{{\Omega}} (1-|u|^2)^2 (1+t \mathrm{div} \eta +\frac{t^2}{2}\mathrm{div} \zeta +t^2 \det \mathrm{D} \eta)+O(t^3). \end{align} $$
Putting together (2.8), (2.9), and (2.10) yields the result.
Similar but simpler computations give the following:
Proposition 2.3 Let
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
and let
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
and let
![]() $(u,A)\in X$
. Then, with definitions (1.14) and (1.15), we have
$(u,A)\in X$
. Then, with definitions (1.14) and (1.15), we have
It can be seen that
![]() $\mathrm {GL}_{\varepsilon }$
is infinitely Gâteaux-differentiable on X, and its first and second variations are given in the following proposition.
$\mathrm {GL}_{\varepsilon }$
is infinitely Gâteaux-differentiable on X, and its first and second variations are given in the following proposition.
Proposition 2.4 The first and second outer variations of
![]() $\mathrm {GL}_{\varepsilon }$
at
$\mathrm {GL}_{\varepsilon }$
at
![]() $(u,A)$
with respect to
$(u,A)$
with respect to
![]() $(v,B)\in {\mathcal C}^{\infty }(\overline {{{\Omega }}},\mathbb {R}^2)\times {\mathcal C}^{\infty }_c(\mathbb {R}^2,\mathbb {R}^2)$
, defined in (1.3)-(1.7) are given by
$(v,B)\in {\mathcal C}^{\infty }(\overline {{{\Omega }}},\mathbb {R}^2)\times {\mathcal C}^{\infty }_c(\mathbb {R}^2,\mathbb {R}^2)$
, defined in (1.3)-(1.7) are given by
 $$ \begin{align*} \mathrm{d} \mathrm{GL}_{\varepsilon} (u,A,v,B) &= \int_{{\Omega}} (\mathrm{D} u-u^{\perp} A^T) :(\mathrm{D} v-v^{\perp} A^T)-(\mathrm{D} u-u^{\perp} A^T):u^{\perp} B^T \\ & \quad +(h-h_{\operatorname{\mathrm{\text{ex}}}})\mathrm{curl\,} B-\frac{1}{{\varepsilon}^2}(1-|u|^2)u\cdot v \end{align*} $$
$$ \begin{align*} \mathrm{d} \mathrm{GL}_{\varepsilon} (u,A,v,B) &= \int_{{\Omega}} (\mathrm{D} u-u^{\perp} A^T) :(\mathrm{D} v-v^{\perp} A^T)-(\mathrm{D} u-u^{\perp} A^T):u^{\perp} B^T \\ & \quad +(h-h_{\operatorname{\mathrm{\text{ex}}}})\mathrm{curl\,} B-\frac{1}{{\varepsilon}^2}(1-|u|^2)u\cdot v \end{align*} $$
 $$ \begin{align*} \mathrm{d}^2\mathrm{GL}_{\varepsilon} (u,A,v,B)&= \int_{{\Omega}} |\mathrm{D} \varphi-u^{\perp} B^T-v^{\perp} A^T|^2+2(\mathrm{D} u-u^{\perp} A^T):v^{\perp} B^T+(\mathrm{curl\,} B)^2 \\ & \quad \quad +\frac{1}{{\varepsilon}^2}(1-|u|^2)|v|^2-\frac{2}{{\varepsilon}^2}(u\cdot v). \end{align*} $$
$$ \begin{align*} \mathrm{d}^2\mathrm{GL}_{\varepsilon} (u,A,v,B)&= \int_{{\Omega}} |\mathrm{D} \varphi-u^{\perp} B^T-v^{\perp} A^T|^2+2(\mathrm{D} u-u^{\perp} A^T):v^{\perp} B^T+(\mathrm{curl\,} B)^2 \\ & \quad \quad +\frac{1}{{\varepsilon}^2}(1-|u|^2)|v|^2-\frac{2}{{\varepsilon}^2}(u\cdot v). \end{align*} $$
The first and second outer variations of
![]() $E_{\varepsilon }$
at u with respect to
$E_{\varepsilon }$
at u with respect to
![]() $v\in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, defined in an analogous manner as for
$v\in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, defined in an analogous manner as for
![]() $\mathrm {GL}_{\varepsilon }$
, are given by
$\mathrm {GL}_{\varepsilon }$
, are given by
Now we give a link between inner and outer variations when these quantities are computed at a smooth point. This link was previously observed in [Reference Le22, Reference Le23, Reference Le and Sternberg24].
Proposition 2.5 Let
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
and let
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
and let
![]() $ (u,A)\in X \cap ({\mathcal C}^3({{\Omega }},\mathbb {R}^2))^2$
then
$ (u,A)\in X \cap ({\mathcal C}^3({{\Omega }},\mathbb {R}^2))^2$
then
 $$ \begin{align*} \delta^2\mathrm{GL}_{\varepsilon} (u,A,\eta)&= \mathrm{d} \mathrm{GL}_{\varepsilon} \left(u,A,\mathrm{D}^2u[\eta,\eta]+\mathrm{D} u .\zeta, \ \mathrm{D}^2A[\eta,\eta]+\mathrm{D} A .\zeta+\mathrm{D} \zeta ^T.A+2\mathrm{D} \eta^T \mathrm{D} A.\eta \right) \\ &\phantom{aaa} +\mathrm{d}^2\mathrm{GL}_{\varepsilon}\left(u,A,-\mathrm{D} u. \eta,-\mathrm{D} A.\eta+\mathrm{D} \eta^T.A\right). \end{align*} $$
$$ \begin{align*} \delta^2\mathrm{GL}_{\varepsilon} (u,A,\eta)&= \mathrm{d} \mathrm{GL}_{\varepsilon} \left(u,A,\mathrm{D}^2u[\eta,\eta]+\mathrm{D} u .\zeta, \ \mathrm{D}^2A[\eta,\eta]+\mathrm{D} A .\zeta+\mathrm{D} \zeta ^T.A+2\mathrm{D} \eta^T \mathrm{D} A.\eta \right) \\ &\phantom{aaa} +\mathrm{d}^2\mathrm{GL}_{\varepsilon}\left(u,A,-\mathrm{D} u. \eta,-\mathrm{D} A.\eta+\mathrm{D} \eta^T.A\right). \end{align*} $$
If
![]() $u \in H^1({{\Omega }},\mathbb {R}^2)\cap {\mathcal C}^3({{\Omega }},\mathbb {R}^2)$
then
$u \in H^1({{\Omega }},\mathbb {R}^2)\cap {\mathcal C}^3({{\Omega }},\mathbb {R}^2)$
then
Proof We first show that, for
![]() $V\in {\mathcal C}^3({{\Omega }},\mathbb {R}^2)$
, we have
$V\in {\mathcal C}^3({{\Omega }},\mathbb {R}^2)$
, we have
with
![]() $X_0=\mathrm {D} ^2V[\eta ,\eta ]+\mathrm {D} V \mathrm {D} \eta $
. In order to do that, we use the following Taylor expansion:
$X_0=\mathrm {D} ^2V[\eta ,\eta ]+\mathrm {D} V \mathrm {D} \eta $
. In order to do that, we use the following Taylor expansion:
 $$ \begin{align*} V\circ \Phi_t^{-1}(y)&=V(y)+t\partial_t|_{t=0} (V\circ \Phi_t^{-1})(y) +\frac{t^2}{2}\partial^2_{tt}|_{t=0}(V\circ \Phi_t^{-1})(y)+O(t^3)\\ &=V(y)+t\mathrm{D} V(y).\partial_t|_{t=0} \Phi_t^{-1}(y)+\frac{t^2}{2}\Big(\mathrm{D} ^2V(y)[\partial_t|_{t=0} \Phi_t^{-1}(y),\partial_t|_{t=0} \Phi_t^{-1}(y)] \\ &\quad +\mathrm{D} V(y).\partial^2_{tt}|_{t=0}\Phi_t^{-1}(y)\Big)+O(t^3). \end{align*} $$
$$ \begin{align*} V\circ \Phi_t^{-1}(y)&=V(y)+t\partial_t|_{t=0} (V\circ \Phi_t^{-1})(y) +\frac{t^2}{2}\partial^2_{tt}|_{t=0}(V\circ \Phi_t^{-1})(y)+O(t^3)\\ &=V(y)+t\mathrm{D} V(y).\partial_t|_{t=0} \Phi_t^{-1}(y)+\frac{t^2}{2}\Big(\mathrm{D} ^2V(y)[\partial_t|_{t=0} \Phi_t^{-1}(y),\partial_t|_{t=0} \Phi_t^{-1}(y)] \\ &\quad +\mathrm{D} V(y).\partial^2_{tt}|_{t=0}\Phi_t^{-1}(y)\Big)+O(t^3). \end{align*} $$
We first compute the derivatives with respect to t of
![]() $\Phi _t^{-1}$
. We use the expansion of
$\Phi _t^{-1}$
. We use the expansion of
![]() $\Phi _t$
given in (2.4) and the relation
$\Phi _t$
given in (2.4) and the relation
Differentiating with respect to t yields
and evaluating at
![]() $t=0$
, we find that
$t=0$
, we find that
![]() $\partial _t|_{t=0}\Phi _t^{-1}(x)=-\eta (x)$
. We can differentiate once more with respect to t to obtain
$\partial _t|_{t=0}\Phi _t^{-1}(x)=-\eta (x)$
. We can differentiate once more with respect to t to obtain
Evaluating at
![]() $t=0$
and using the expression previously found for
$t=0$
and using the expression previously found for
![]() $\partial _t|_{t=0}\Phi _t^{-1}(x)$
, we arrive at
$\partial _t|_{t=0}\Phi _t^{-1}(x)$
, we arrive at
![]() $ \partial ^2_{tt}|_{t=0}\Phi _t^{-1}(x)=\mathrm {D} \eta (x).\eta (x)$
. By the Taylor formula with integral remainder, we know that
$ \partial ^2_{tt}|_{t=0}\Phi _t^{-1}(x)=\mathrm {D} \eta (x).\eta (x)$
. By the Taylor formula with integral remainder, we know that
and we can check that we can differentiate under the integral sign giving the term in
![]() $O(t^3)$
to obtain also that
$O(t^3)$
to obtain also that
![]() $\mathrm {D} \Phi _t^{-1}(x)=\mathrm {Id}-t\mathrm {D} \eta (x)+\frac {t^2}{2}\mathrm {D} \zeta (x)+O(t^3)$
, where
$\mathrm {D} \Phi _t^{-1}(x)=\mathrm {Id}-t\mathrm {D} \eta (x)+\frac {t^2}{2}\mathrm {D} \zeta (x)+O(t^3)$
, where
![]() $\zeta (x)=\mathrm {D} \eta (x).\eta (x)$
. Thus, we obtain
$\zeta (x)=\mathrm {D} \eta (x).\eta (x)$
. Thus, we obtain
Now we recall from (2.3) that, with some abuse of notation,
![]() $ (\Phi _t^{-1})^*A=\mathrm {D} \Phi _t^{-T} (A\circ \Phi _t^{-1})$
. Thus, by using the formula (2.11), we can write
$ (\Phi _t^{-1})^*A=\mathrm {D} \Phi _t^{-T} (A\circ \Phi _t^{-1})$
. Thus, by using the formula (2.11), we can write
 $$ \begin{align*} (\Phi_t^{-1})^*A &=\left(\mathrm{Id}-t\mathrm{D} \eta (x)+\frac{t^2}{2}\mathrm{D} \zeta (x)+O(t^3) \right)^T \nonumber\\ & \quad \quad \times\Big( A-t\mathrm{D} A. \eta+\frac{t^2}{2}(\mathrm{D}^2A[\eta,\eta]+\mathrm{D} A. \zeta )+O(t^3)\Big) \nonumber \\ &= A-t(\mathrm{D} A.\zeta+(\mathrm{D} \eta)^T.A) \\ &\quad \quad +\frac{t^2}{2}\Big( \mathrm{D}^2A[\eta,\eta]+\mathrm{D} A. \zeta +\mathrm{D} \zeta^T.A+2\mathrm{D} \eta^T .(\mathrm{D} A .\eta) \Big) +O(t^3). \end{align*} $$
$$ \begin{align*} (\Phi_t^{-1})^*A &=\left(\mathrm{Id}-t\mathrm{D} \eta (x)+\frac{t^2}{2}\mathrm{D} \zeta (x)+O(t^3) \right)^T \nonumber\\ & \quad \quad \times\Big( A-t\mathrm{D} A. \eta+\frac{t^2}{2}(\mathrm{D}^2A[\eta,\eta]+\mathrm{D} A. \zeta )+O(t^3)\Big) \nonumber \\ &= A-t(\mathrm{D} A.\zeta+(\mathrm{D} \eta)^T.A) \\ &\quad \quad +\frac{t^2}{2}\Big( \mathrm{D}^2A[\eta,\eta]+\mathrm{D} A. \zeta +\mathrm{D} \zeta^T.A+2\mathrm{D} \eta^T .(\mathrm{D} A .\eta) \Big) +O(t^3). \end{align*} $$
Thus, if we let
![]() $ (u_t,A_t):= (u\circ \Phi _t^{-1},(\Phi _t^{1})^*A)$
, by using (2.12) applied to
$ (u_t,A_t):= (u\circ \Phi _t^{-1},(\Phi _t^{1})^*A)$
, by using (2.12) applied to
![]() $V=u$
and by assuming that
$V=u$
and by assuming that
![]() $ (u,A)\in ({\mathcal C}^{\infty }({{\Omega }},\mathbb {R}^2))^2$
, we find that
$ (u,A)\in ({\mathcal C}^{\infty }({{\Omega }},\mathbb {R}^2))^2$
, we find that
 $$ \begin{align*} \mathrm{GL}_{\varepsilon}(u_t,A_t)&=\mathrm{GL}_{\varepsilon}\Big(u-t\mathrm{D} u. \eta +\frac{t^2}{2}(\mathrm{D} ^2u[\eta,\eta]+\mathrm{D} u)+O(t^3),A-t(\mathrm{D} A. \eta+\mathrm{D} \eta^T.A) \\ & \quad +\frac{t^2}{2}\left(\mathrm{D} ^2A[\eta,\eta]+\mathrm{D} A. \zeta+\mathrm{D} \zeta^T.A+2\mathrm{D} \eta^T.(\mathrm{D} A.\eta)\right)+O(t^3) \Big) \\ &=\mathrm{GL}_{\varepsilon}(u,A)+t\mathrm{d} \mathrm{GL}_{\varepsilon}(u,A,-\mathrm{D} u.\eta,-\mathrm{D} A.\eta+(\mathrm{D} \eta)^TA) \\ &\quad +\frac{t^2}{2}\mathrm{d} \mathrm{GL}_{\varepsilon} \bigl(u,A,\mathrm{D} ^2u[\eta,\eta]+\mathrm{D} u. \zeta,\mathrm{D} ^2A[\eta,\eta]+\mathrm{D} A. \zeta+\mathrm{D} \zeta^T.A+2\mathrm{D} \eta^T.(\mathrm{D} A.\eta)\bigr) \\ &\quad +\frac{t^2}{2}\mathrm{d}^2\mathrm{GL}_{\varepsilon}(u,A)(-\mathrm{D} u.\eta,-\mathrm{D} A.\eta+\mathrm{D} \eta)^T.A) +O(t^3). \end{align*} $$
$$ \begin{align*} \mathrm{GL}_{\varepsilon}(u_t,A_t)&=\mathrm{GL}_{\varepsilon}\Big(u-t\mathrm{D} u. \eta +\frac{t^2}{2}(\mathrm{D} ^2u[\eta,\eta]+\mathrm{D} u)+O(t^3),A-t(\mathrm{D} A. \eta+\mathrm{D} \eta^T.A) \\ & \quad +\frac{t^2}{2}\left(\mathrm{D} ^2A[\eta,\eta]+\mathrm{D} A. \zeta+\mathrm{D} \zeta^T.A+2\mathrm{D} \eta^T.(\mathrm{D} A.\eta)\right)+O(t^3) \Big) \\ &=\mathrm{GL}_{\varepsilon}(u,A)+t\mathrm{d} \mathrm{GL}_{\varepsilon}(u,A,-\mathrm{D} u.\eta,-\mathrm{D} A.\eta+(\mathrm{D} \eta)^TA) \\ &\quad +\frac{t^2}{2}\mathrm{d} \mathrm{GL}_{\varepsilon} \bigl(u,A,\mathrm{D} ^2u[\eta,\eta]+\mathrm{D} u. \zeta,\mathrm{D} ^2A[\eta,\eta]+\mathrm{D} A. \zeta+\mathrm{D} \zeta^T.A+2\mathrm{D} \eta^T.(\mathrm{D} A.\eta)\bigr) \\ &\quad +\frac{t^2}{2}\mathrm{d}^2\mathrm{GL}_{\varepsilon}(u,A)(-\mathrm{D} u.\eta,-\mathrm{D} A.\eta+\mathrm{D} \eta)^T.A) +O(t^3). \end{align*} $$
By identification, we conclude. A density argument allows us to extend this result for
![]() $ (u,A)\in ({\mathcal C}^3({{\Omega }},\mathbb {R}^2))^2$
. Similar computations for
$ (u,A)\in ({\mathcal C}^3({{\Omega }},\mathbb {R}^2))^2$
. Similar computations for
![]() $E_{\varepsilon }$
give the result.
$E_{\varepsilon }$
give the result.
Since critical points of the GL energy in the Coulomb gauge are smooth, we can use Proposition 2.5, and we can deduce that stable critical points of
![]() $\mathrm {GL}_{\varepsilon }$
satisfy that they have a nonnegative second inner variation. This is summarized in the following corollary.
$\mathrm {GL}_{\varepsilon }$
satisfy that they have a nonnegative second inner variation. This is summarized in the following corollary.
Corollary 2.6 Let
![]() $ (u,A)$
be in X such that
$ (u,A)$
be in X such that
![]() $\mathrm {d} \mathrm {GL}_{\varepsilon }(u,A,v,B)=0$
for any
$\mathrm {d} \mathrm {GL}_{\varepsilon }(u,A,v,B)=0$
for any
![]() $(v,B)\in ({\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2))^2$
and with A in the Coulomb gauge, then
$(v,B)\in ({\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2))^2$
and with A in the Coulomb gauge, then
![]() $\delta \mathrm {GL}_{\varepsilon }(u,\eta )=0$
for any
$\delta \mathrm {GL}_{\varepsilon }(u,\eta )=0$
for any
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
. If we assume furthermore that
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
. If we assume furthermore that
![]() $\mathrm {d}^2\mathrm {GL}_{\varepsilon }(u,A,v,B)\geq 0$
for any
$\mathrm {d}^2\mathrm {GL}_{\varepsilon }(u,A,v,B)\geq 0$
for any
![]() $ (v,B)\in ({\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2))^2$
, then
$ (v,B)\in ({\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2))^2$
, then
![]() $ \delta ^2 \mathrm {GL}_{\varepsilon }(u,A,\eta ) \geq 0$
for any
$ \delta ^2 \mathrm {GL}_{\varepsilon }(u,A,\eta ) \geq 0$
for any
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
. Similar results hold for the nonmagnetic GL energy.
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
. Similar results hold for the nonmagnetic GL energy.
2.3 Some remarks about inner variations
The link between inner and outer variations for regular argument was already observed in [Reference Le22, Reference Le23, Reference Le and Sternberg24]. In order to make a direct link between the first and second inner variations when the argument is regular, one can also use that for
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
and integrate by parts several times.
To examine the difference between inner and outer variations from the point of view of stability, we can start by considering the 1D case. Let
![]() ${{\Omega }}=(a,b)\subset \mathbb {R}$
be an open interval with
${{\Omega }}=(a,b)\subset \mathbb {R}$
be an open interval with
![]() $a<b$
. By using, for example, [Reference Le and Sternberg24, Lemma 2.4], we can show that for an energy of the form
$a<b$
. By using, for example, [Reference Le and Sternberg24, Lemma 2.4], we can show that for an energy of the form
![]() $ \mathcal {E}(V)=\int _a^b F(V,V')=\int _a^b \left (|V'|^2/2+f(V)\right ) \mathrm {d} x$
with
$ \mathcal {E}(V)=\int _a^b F(V,V')=\int _a^b \left (|V'|^2/2+f(V)\right ) \mathrm {d} x$
with
![]() $f:\mathbb {R}\rightarrow \mathbb {R}$
a smooth function, the second inner variation is given by
$f:\mathbb {R}\rightarrow \mathbb {R}$
a smooth function, the second inner variation is given by
for all
![]() $\eta \in {\mathcal C}^{\infty }_c((a,b),\mathbb {R})$
. Surprisingly, this quantity does not depend on f and is always nonnegative. This allows us to recover the following known result about strictly monotone solutions of ODEs in 1D.
$\eta \in {\mathcal C}^{\infty }_c((a,b),\mathbb {R})$
. Surprisingly, this quantity does not depend on f and is always nonnegative. This allows us to recover the following known result about strictly monotone solutions of ODEs in 1D.
Proposition 2.7 Let
![]() $V\in {\mathcal C}^2((a,b),\mathbb {R})$
be a critical point of
$V\in {\mathcal C}^2((a,b),\mathbb {R})$
be a critical point of
![]() $\mathcal {E}(V)=\int _a^b \left (|V'|^2/2+f(V)\right ) $
with
$\mathcal {E}(V)=\int _a^b \left (|V'|^2/2+f(V)\right ) $
with
![]() $f\in {\mathcal C}^{\infty }(\mathbb {R},\mathbb {R})$
(i.e., a solution of
$f\in {\mathcal C}^{\infty }(\mathbb {R},\mathbb {R})$
(i.e., a solution of
![]() $-V"+f'(V)=0$
in
$-V"+f'(V)=0$
in
![]() $(a,b)$
). Assume furthermore that V is strictly monotone. Then V is stable; that is,
$(a,b)$
). Assume furthermore that V is strictly monotone. Then V is stable; that is,
Proof We first observe that V is in
![]() ${\mathcal C}^{\infty }( (a,b)$
. Then every
${\mathcal C}^{\infty }( (a,b)$
. Then every
![]() $\varphi \in {\mathcal C}^{\infty }_c((a,b))$
can be written as
$\varphi \in {\mathcal C}^{\infty }_c((a,b))$
can be written as
![]() $ \varphi =V'\eta $
since
$ \varphi =V'\eta $
since
![]() $V'$
does not vanish in
$V'$
does not vanish in
![]() $(a,b)$
. We can thus use a result analogous to Proposition 2.5 – see, for example, [Reference Le and Sternberg24, Corollary 2.3] – and the fact that
$(a,b)$
. We can thus use a result analogous to Proposition 2.5 – see, for example, [Reference Le and Sternberg24, Corollary 2.3] – and the fact that
![]() $ \mathrm {d} E(V, \mathrm {D}^2V[\eta ,\eta ]+\mathrm {D} V. (\mathrm {D} \eta. \eta ))=0$
since
$ \mathrm {d} E(V, \mathrm {D}^2V[\eta ,\eta ]+\mathrm {D} V. (\mathrm {D} \eta. \eta ))=0$
since
![]() $\mathrm {D}^2V[\eta ,\eta ]+\mathrm {D} V. (\mathrm {D} \eta. \eta ) \in {\mathcal C}^{\infty }_c( (a,b),\mathbb {R})$
to conclude that
$\mathrm {D}^2V[\eta ,\eta ]+\mathrm {D} V. (\mathrm {D} \eta. \eta ) \in {\mathcal C}^{\infty }_c( (a,b),\mathbb {R})$
to conclude that
for all
![]() $\varphi \in {\mathcal C}^{\infty }_c((a,b))$
.
$\varphi \in {\mathcal C}^{\infty }_c((a,b))$
.
For a classical proof of the above fact, we refer to Proposition 1.2.1 and Definition 1.2.1 in [Reference Dupaigne14].
3 Passing to the limit in the second inner variation
From the expression of the second inner variation of
![]() $\mathrm {GL}_{\varepsilon }$
given in Proposition 2.2, it appears that to understand the limit of
$\mathrm {GL}_{\varepsilon }$
given in Proposition 2.2, it appears that to understand the limit of
![]() $\delta ^2\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon },\eta )/h_{\operatorname {\mathrm {\text {ex}}}}^2$
for
$\delta ^2\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon },\eta )/h_{\operatorname {\mathrm {\text {ex}}}}^2$
for
![]() $ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
a family of critical points of the GL energy, we need to understand the limit of all the quadratic terms in the derivatives
$ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
a family of critical points of the GL energy, we need to understand the limit of all the quadratic terms in the derivatives
![]() $|\partial _1^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2, |\partial _2^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2$
and
$|\partial _1^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2, |\partial _2^{A_{\varepsilon }}u_{\varepsilon }|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2$
and
![]() $ \langle \partial _1^{A_{\varepsilon }}u_{\varepsilon }, \partial _2^{A_{\varepsilon }} u_{\varepsilon }\rangle /h_{\operatorname {\mathrm {\text {ex}}}}^2$
. This is the object of this section.
$ \langle \partial _1^{A_{\varepsilon }}u_{\varepsilon }, \partial _2^{A_{\varepsilon }} u_{\varepsilon }\rangle /h_{\operatorname {\mathrm {\text {ex}}}}^2$
. This is the object of this section.
3.1 The case with magnetic field
The following proposition is mainly the lower-bound for the
![]() $\Gamma $
-convergence result of
$\Gamma $
-convergence result of
![]() $\mathrm {GL}_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}^2$
obtained in [Reference Sandier and Serfaty32]. We present the proof here to underline the fact that, thanks to assumption (H), we know the limit of the energy density.
$\mathrm {GL}_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}^2$
obtained in [Reference Sandier and Serfaty32]. We present the proof here to underline the fact that, thanks to assumption (H), we know the limit of the energy density.
Proposition 3.1 Let
![]() $ \{ (u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of critical points of
$ \{ (u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of critical points of
![]() $\mathrm {GL}_{\varepsilon }$
satisfying (1.8)-(1.9). We set
$\mathrm {GL}_{\varepsilon }$
satisfying (1.8)-(1.9). We set
![]() $j_{\varepsilon }=\langle iu_{\varepsilon },(\nabla -iA_{\varepsilon })u_{\varepsilon }\rangle $
and
$j_{\varepsilon }=\langle iu_{\varepsilon },(\nabla -iA_{\varepsilon })u_{\varepsilon }\rangle $
and
![]() $h_{\varepsilon }=\mathrm {curl\,} A_{\varepsilon }$
.
$h_{\varepsilon }=\mathrm {curl\,} A_{\varepsilon }$
.
-
1) Up to a subsequence,
for every $$ \begin{align*} \frac{\mu(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}}:=\frac{\mathrm{curl\,} (j_{\varepsilon}+A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}} \xrightarrow[{\varepsilon} \to 0]{} \mu \quad \text{ in } \left( {\mathcal C}^{0,\gamma}({{\Omega}})\right)^* \end{align*} $$
$$ \begin{align*} \frac{\mu(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}}:=\frac{\mathrm{curl\,} (j_{\varepsilon}+A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}} \xrightarrow[{\varepsilon} \to 0]{} \mu \quad \text{ in } \left( {\mathcal C}^{0,\gamma}({{\Omega}})\right)^* \end{align*} $$
 $\gamma \in (0,1)$
and with
$\gamma \in (0,1)$
and with
 $-\nabla ^{\perp } h=j$
and
$-\nabla ^{\perp } h=j$
and
 $\mu =-\Delta h+h$
. Furthermore,
$\mu =-\Delta h+h$
. Furthermore,  $$ \begin{align*} \liminf_{{\varepsilon} \to 0} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &\geq \liminf_{{\varepsilon} \to 0} \frac{1}{2h_{\operatorname{\mathrm{\text{ex}}}}^2}\int_{{\Omega}} \left( |\nabla h_{\varepsilon}|^2+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \right) \\ & \geq \frac{|\mu|({{\Omega}})}{2\lambda}+\frac12 \int_{{\Omega}} \left( |\nabla h|^2+|h-1|^2\right). \end{align*} $$
$$ \begin{align*} \liminf_{{\varepsilon} \to 0} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &\geq \liminf_{{\varepsilon} \to 0} \frac{1}{2h_{\operatorname{\mathrm{\text{ex}}}}^2}\int_{{\Omega}} \left( |\nabla h_{\varepsilon}|^2+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \right) \\ & \geq \frac{|\mu|({{\Omega}})}{2\lambda}+\frac12 \int_{{\Omega}} \left( |\nabla h|^2+|h-1|^2\right). \end{align*} $$
-
2) We set
 $ g_{\varepsilon }(u_{\varepsilon },A_{\varepsilon }) := \frac 12 \left ( |\nabla u_{\varepsilon }|^2+|h_{\varepsilon }-h_{\operatorname {\mathrm {\text {ex}}}}|^2+\frac {1}{2{\varepsilon }^2}(1-|u_{\varepsilon }|^2)^2 \right )$
. Let us assume that (H) holds then, (3.1)
$ g_{\varepsilon }(u_{\varepsilon },A_{\varepsilon }) := \frac 12 \left ( |\nabla u_{\varepsilon }|^2+|h_{\varepsilon }-h_{\operatorname {\mathrm {\text {ex}}}}|^2+\frac {1}{2{\varepsilon }^2}(1-|u_{\varepsilon }|^2)^2 \right )$
. Let us assume that (H) holds then, (3.1) $$ \begin{align} \frac{g_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup \frac{1}{2\lambda}|\mu|+\frac{1}{2}\left( |\nabla h|^2+|h-1|^2\right) \text{ in } {\mathcal M}({{\Omega}}), \end{align} $$
(3.2)and
$$ \begin{align} \frac{g_{\varepsilon}(u_{\varepsilon},A_{\varepsilon})}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup \frac{1}{2\lambda}|\mu|+\frac{1}{2}\left( |\nabla h|^2+|h-1|^2\right) \text{ in } {\mathcal M}({{\Omega}}), \end{align} $$
(3.2)and $$ \begin{align} \frac{|\nabla h_{\varepsilon}|^2}{|u_{\varepsilon}|^2h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\nabla h|^2+\frac{1}{\lambda}|\mu|, \quad \frac{|\nabla h_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\nabla h|^2+\frac{1}{\lambda}|\mu|, \quad \frac{|\nabla_{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\nabla h|^2+\frac{1}{\lambda}|\mu| \end{align} $$
(3.3)
$$ \begin{align} \frac{|\nabla h_{\varepsilon}|^2}{|u_{\varepsilon}|^2h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\nabla h|^2+\frac{1}{\lambda}|\mu|, \quad \frac{|\nabla h_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\nabla h|^2+\frac{1}{\lambda}|\mu|, \quad \frac{|\nabla_{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\nabla h|^2+\frac{1}{\lambda}|\mu| \end{align} $$
(3.3) $$ \begin{align} \frac{1}{h_{\operatorname{\mathrm{\text{ex}}}}^2}\left(|\nabla |u_{\varepsilon}||^2+\frac{1}{2{\varepsilon}^2}(1-|u|^2)^2 \right) \rightharpoonup 0\ \text{ in } {\mathcal M}({{\Omega}}). \end{align} $$
$$ \begin{align} \frac{1}{h_{\operatorname{\mathrm{\text{ex}}}}^2}\left(|\nabla |u_{\varepsilon}||^2+\frac{1}{2{\varepsilon}^2}(1-|u|^2)^2 \right) \rightharpoonup 0\ \text{ in } {\mathcal M}({{\Omega}}). \end{align} $$
Proof We recall that if
![]() $ (u,A)$
is a solution to (1.4), then
$ (u,A)$
is a solution to (1.4), then
![]() $|u|\leq 1$
in
$|u|\leq 1$
in
![]() ${{\Omega }}$
; see, for example, [Reference Sandier and Serfaty32, Chapter 3]. We also observe that near points where u does not vanish, we can write
${{\Omega }}$
; see, for example, [Reference Sandier and Serfaty32, Chapter 3]. We also observe that near points where u does not vanish, we can write
![]() $u=\rho e^{i \varphi }$
. Even if the phase
$u=\rho e^{i \varphi }$
. Even if the phase
![]() $\varphi $
is not globally defined, it can be seen that its gradient is globally defined. Using the second equation in (1.4), we find that
$\varphi $
is not globally defined, it can be seen that its gradient is globally defined. Using the second equation in (1.4), we find that
We can also see that
 $$ \begin{align} \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon}) &= \frac12 \int_{{\Omega}} |\nabla |u_{\varepsilon}||^2+|u_{\varepsilon}|^2|\nabla \varphi_{\varepsilon}-A_{\varepsilon}|^2+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2+\frac{1}{2{\varepsilon}^2}(1-|u_{\varepsilon}|^2)^2 \nonumber \\ &=\frac12 \int_{{\Omega}} |\nabla |u_{\varepsilon}||^2+\frac{|\nabla h_{\varepsilon}|^2}{|u_{\varepsilon}|^2}+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2+\frac{1}{2{\varepsilon}^2}(1-|u_{\varepsilon}|^2)^2 \end{align} $$
$$ \begin{align} \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon}) &= \frac12 \int_{{\Omega}} |\nabla |u_{\varepsilon}||^2+|u_{\varepsilon}|^2|\nabla \varphi_{\varepsilon}-A_{\varepsilon}|^2+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2+\frac{1}{2{\varepsilon}^2}(1-|u_{\varepsilon}|^2)^2 \nonumber \\ &=\frac12 \int_{{\Omega}} |\nabla |u_{\varepsilon}||^2+\frac{|\nabla h_{\varepsilon}|^2}{|u_{\varepsilon}|^2}+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2+\frac{1}{2{\varepsilon}^2}(1-|u_{\varepsilon}|^2)^2 \end{align} $$
Then, we can use the energy bound
![]() $\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon })\leq C h_{\operatorname {\mathrm {\text {ex}}}}^2$
to deduce that
$\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon })\leq C h_{\operatorname {\mathrm {\text {ex}}}}^2$
to deduce that
![]() $ h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
is bounded in
$ h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
is bounded in
![]() $H^1({{\Omega }})$
and thus converges weakly in that space, up to a subsequence, to some
$H^1({{\Omega }})$
and thus converges weakly in that space, up to a subsequence, to some
![]() $h\in H^1({{\Omega }})$
. We also observe that, since we consider solutions to (1.4), then
$h\in H^1({{\Omega }})$
. We also observe that, since we consider solutions to (1.4), then
![]() $j_{\varepsilon }=-\nabla ^{\perp } h_{\varepsilon }$
and
$j_{\varepsilon }=-\nabla ^{\perp } h_{\varepsilon }$
and
![]() $\mu (u_{\varepsilon },A_{\varepsilon })=\mathrm { curl\,} j_{\varepsilon }+h_{\varepsilon }=-\Delta h_{\varepsilon }+h_{\varepsilon } \rightharpoonup -\Delta h+h=\mu $
in
$\mu (u_{\varepsilon },A_{\varepsilon })=\mathrm { curl\,} j_{\varepsilon }+h_{\varepsilon }=-\Delta h_{\varepsilon }+h_{\varepsilon } \rightharpoonup -\Delta h+h=\mu $
in
![]() $H^{-1}({{\Omega }})$
. We now show the convergence of
$H^{-1}({{\Omega }})$
. We now show the convergence of
![]() $\mu _{\varepsilon }:=\mu (u_{\varepsilon },A_{\varepsilon })$
in
$\mu _{\varepsilon }:=\mu (u_{\varepsilon },A_{\varepsilon })$
in
![]() $({\mathcal C}^{0,\gamma }({{\Omega }}))^*$
and the lower bound. Since we assume in (1.9) that
$({\mathcal C}^{0,\gamma }({{\Omega }}))^*$
and the lower bound. Since we assume in (1.9) that
![]() $h_{\operatorname {\mathrm {\text {ex}}}}\leq C |\log {\varepsilon }|$
, we have from (1.8) that
$h_{\operatorname {\mathrm {\text {ex}}}}\leq C |\log {\varepsilon }|$
, we have from (1.8) that
![]() $\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon })\leq Ch_{\operatorname {\mathrm {\text {ex}}}}^2\leq C|\log {\varepsilon }|^2$
. We can then apply Proposition 1.1 in [Reference Sandier and Serfaty29] (see also [Reference Sandier and Serfaty32, Theorem 4.1])Footnote
3
to find a family of balls (depending on
$\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon })\leq Ch_{\operatorname {\mathrm {\text {ex}}}}^2\leq C|\log {\varepsilon }|^2$
. We can then apply Proposition 1.1 in [Reference Sandier and Serfaty29] (see also [Reference Sandier and Serfaty32, Theorem 4.1])Footnote
3
to find a family of balls (depending on
![]() ${\varepsilon }$
)
${\varepsilon }$
)
![]() $ (B_i)_{i\in I_{\varepsilon }}=(B(a_i,r_i))_{i\in I_{\varepsilon }}$
such that
$ (B_i)_{i\in I_{\varepsilon }}=(B(a_i,r_i))_{i\in I_{\varepsilon }}$
such that
with
![]() $h_{\varepsilon }=\mathrm {curl\,} A_{\varepsilon }$
,
$h_{\varepsilon }=\mathrm {curl\,} A_{\varepsilon }$
,
![]() $ d_i=\deg (\frac {u_{\varepsilon }}{|u_{\varepsilon }|},\partial B_i)$
if
$ d_i=\deg (\frac {u_{\varepsilon }}{|u_{\varepsilon }|},\partial B_i)$
if
![]() $\overline {B}_i \subset {{\Omega }}$
and
$\overline {B}_i \subset {{\Omega }}$
and
![]() $0$
otherwise.
$0$
otherwise.
We let
![]() $V_{\varepsilon } := \bigcup _{i\in I_{\varepsilon }} B_i$
. Then by using (3.5), we find
$V_{\varepsilon } := \bigcup _{i\in I_{\varepsilon }} B_i$
. Then by using (3.5), we find
Note that (3.5) and (1.8) imply that
![]() $\sum _{i\in I_{\varepsilon }} |d_i|\leq C|\log {\varepsilon }|\leq C h_{\operatorname {\mathrm {\text {ex}}}}$
. Now let U be an open sub-domain of
$\sum _{i\in I_{\varepsilon }} |d_i|\leq C|\log {\varepsilon }|\leq C h_{\operatorname {\mathrm {\text {ex}}}}$
. Now let U be an open sub-domain of
![]() ${{\Omega }}$
; working in U will be useful to prove point 2). We can write
${{\Omega }}$
; working in U will be useful to prove point 2). We can write
 $$ \begin{align} \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},U)&=\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},V_{\varepsilon})+\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},U\setminus V_{\varepsilon}) \nonumber \\ & =\frac12 \int_{V_{\varepsilon}} |\nabla h_{\varepsilon}|^2+ \frac12 \int_{U\setminus V_{\varepsilon}} \left(|\nabla h_{\varepsilon}|^2 +|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \right) \end{align} $$
$$ \begin{align} \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},U)&=\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},V_{\varepsilon})+\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},U\setminus V_{\varepsilon}) \nonumber \\ & =\frac12 \int_{V_{\varepsilon}} |\nabla h_{\varepsilon}|^2+ \frac12 \int_{U\setminus V_{\varepsilon}} \left(|\nabla h_{\varepsilon}|^2 +|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \right) \end{align} $$
We divide by
![]() $h_{\operatorname {\mathrm {\text {ex}}}}^2$
to obtain
$h_{\operatorname {\mathrm {\text {ex}}}}^2$
to obtain
 $$ \begin{align} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},U)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} & \geq \frac{1}{2h_{\operatorname{\mathrm{\text{ex}}}}^2} \int_U |\nabla h_{\varepsilon}|^2+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \\ &\geq \pi \frac{\sum_i |d_i|}{h_{\operatorname{\mathrm{\text{ex}}}}} \frac{|\log {\varepsilon}|}{h_{\operatorname{\mathrm{\text{ex}}}}} +\int_{U\setminus V_{\varepsilon}} \left| \frac{\nabla h_{\varepsilon}}{h_{\operatorname{\mathrm{\text{ex}}}}} \right|^2+\left|\frac{h_{\varepsilon}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2-o(1). \nonumber \end{align} $$
$$ \begin{align} \frac{\mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},U)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} & \geq \frac{1}{2h_{\operatorname{\mathrm{\text{ex}}}}^2} \int_U |\nabla h_{\varepsilon}|^2+|h_{\varepsilon}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \\ &\geq \pi \frac{\sum_i |d_i|}{h_{\operatorname{\mathrm{\text{ex}}}}} \frac{|\log {\varepsilon}|}{h_{\operatorname{\mathrm{\text{ex}}}}} +\int_{U\setminus V_{\varepsilon}} \left| \frac{\nabla h_{\varepsilon}}{h_{\operatorname{\mathrm{\text{ex}}}}} \right|^2+\left|\frac{h_{\varepsilon}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2-o(1). \nonumber \end{align} $$
Since
![]() $\sum _{i\in I_{\varepsilon }} r_i\xrightarrow [{\varepsilon } \to 0]{} 0$
, we can extract a subsequence
$\sum _{i\in I_{\varepsilon }} r_i\xrightarrow [{\varepsilon } \to 0]{} 0$
, we can extract a subsequence
![]() ${\varepsilon }_n \to 0$
such that if we set
${\varepsilon }_n \to 0$
such that if we set
![]() $\mathcal {A}_N:=\bigcup _{n \geq N} V_{{\varepsilon }_n}$
, we have
$\mathcal {A}_N:=\bigcup _{n \geq N} V_{{\varepsilon }_n}$
, we have
![]() $|\mathcal {A}_N|\rightarrow 0$
when
$|\mathcal {A}_N|\rightarrow 0$
when
![]() $N \to +\infty $
. By weak convergence of
$N \to +\infty $
. By weak convergence of
![]() $h_{\varepsilon }$
in
$h_{\varepsilon }$
in
![]() $H^1({{\Omega }})$
, for every N fixed,
$H^1({{\Omega }})$
, for every N fixed,
 $$ \begin{align*} \liminf_{n \to +\infty} \int_{U\setminus V_{{\varepsilon}_n}} \left| \frac{\nabla h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}\right|^2+\left|\frac{h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2 &\geq \liminf_{n \to +\infty} \int_{U\setminus \mathcal{A}_N} \left| \frac{\nabla h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}\right|^2+\left|\frac{h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2 \\ &\geq \int_{U\setminus \mathcal{A}_N} |\nabla h|^2+|h-1|^2. \end{align*} $$
$$ \begin{align*} \liminf_{n \to +\infty} \int_{U\setminus V_{{\varepsilon}_n}} \left| \frac{\nabla h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}\right|^2+\left|\frac{h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2 &\geq \liminf_{n \to +\infty} \int_{U\setminus \mathcal{A}_N} \left| \frac{\nabla h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}\right|^2+\left|\frac{h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2 \\ &\geq \int_{U\setminus \mathcal{A}_N} |\nabla h|^2+|h-1|^2. \end{align*} $$
We then pass to the limit
![]() $N \to +\infty $
to find
$N \to +\infty $
to find
 $$ \begin{align} \liminf_{n \to +\infty} \int_{U\setminus V_{{\varepsilon}_n}} \left| \frac{\nabla h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}\right|^2+\left|\frac{h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2 \geq \int_U |\nabla h|^2+|h-1|^2. \end{align} $$
$$ \begin{align} \liminf_{n \to +\infty} \int_{U\setminus V_{{\varepsilon}_n}} \left| \frac{\nabla h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}\right|^2+\left|\frac{h_{{\varepsilon}_n}}{h_{\operatorname{\mathrm{\text{ex}}}}}-1 \right|^2 \geq \int_U |\nabla h|^2+|h-1|^2. \end{align} $$
However, coming back to (3.7) and using that
![]() $\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon })\leq Ch_{\operatorname {\mathrm {\text {ex}}}}^2$
, we find that
$\mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon })\leq Ch_{\operatorname {\mathrm {\text {ex}}}}^2$
, we find that
![]() $\frac {1}{h_{\operatorname {\mathrm {\text {ex}}}}}\sum _{i\in I}|d_i|$
stays bounded. Hence,
$\frac {1}{h_{\operatorname {\mathrm {\text {ex}}}}}\sum _{i\in I}|d_i|$
stays bounded. Hence,
![]() $\frac {2\pi }{h_{\operatorname {\mathrm {\text {ex}}}}} \sum _{i} d_i \delta _{a_i}$
converges, up to a subsequence in
$\frac {2\pi }{h_{\operatorname {\mathrm {\text {ex}}}}} \sum _{i} d_i \delta _{a_i}$
converges, up to a subsequence in
![]() $ ({\mathcal C}^0_0(U))^*)$
. We then use the Jacobian estimate of Theorem 6.1 in [Reference Sandier and Serfaty32] in U to say that this limit is also the limit of
$ ({\mathcal C}^0_0(U))^*)$
. We then use the Jacobian estimate of Theorem 6.1 in [Reference Sandier and Serfaty32] in U to say that this limit is also the limit of
![]() $\mu _{\varepsilon }$
and thus is equal to
$\mu _{\varepsilon }$
and thus is equal to
![]() $\mu =-\Delta h+h$
. Theorem 6.2 in [Reference Sandier and Serfaty32] applied in
$\mu =-\Delta h+h$
. Theorem 6.2 in [Reference Sandier and Serfaty32] applied in
![]() ${{\Omega }}$
implies that
${{\Omega }}$
implies that
![]() $\mu _{\varepsilon }$
converges toward
$\mu _{\varepsilon }$
converges toward
![]() $\mu $
in
$\mu $
in
![]() $({\mathcal C}^{0,\gamma }_0({{\Omega }}))^*$
. We then pass to the limit in (3.8), and we use (3.9) to obtain
$({\mathcal C}^{0,\gamma }_0({{\Omega }}))^*$
. We then pass to the limit in (3.8), and we use (3.9) to obtain
 $$ \begin{align} \liminf_{n \to +\infty} \frac{\mathrm{GL}_{{\varepsilon}_n}(u_{{\varepsilon}_n},A_{{\varepsilon}_n},U)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &\geq \frac{1}{2h_{\operatorname{\mathrm{\text{ex}}}}^2}\int_U \left( |\nabla h_{{\varepsilon}_n}|^2+|h_{{\varepsilon}_n}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \right) \nonumber \\ & \geq \frac{1}{2\lambda}|\mu|(U)+\frac12 \int_U \left(|\nabla h|^2+|h-1|^2 \right). \end{align} $$
$$ \begin{align} \liminf_{n \to +\infty} \frac{\mathrm{GL}_{{\varepsilon}_n}(u_{{\varepsilon}_n},A_{{\varepsilon}_n},U)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &\geq \frac{1}{2h_{\operatorname{\mathrm{\text{ex}}}}^2}\int_U \left( |\nabla h_{{\varepsilon}_n}|^2+|h_{{\varepsilon}_n}-h_{\operatorname{\mathrm{\text{ex}}}}|^2 \right) \nonumber \\ & \geq \frac{1}{2\lambda}|\mu|(U)+\frac12 \int_U \left(|\nabla h|^2+|h-1|^2 \right). \end{align} $$
This proves point 1).
To prove point 2), we assume that (H) holds. Then we set
We have that
![]() $g_{\varepsilon } ({{\Omega }})\rightarrow \left (\frac {1}{2\lambda }|\mu |+\frac {1}{2}\left ( |\nabla h|^2+|h-1|^2\right ) \right )({{\Omega }})$
and
$g_{\varepsilon } ({{\Omega }})\rightarrow \left (\frac {1}{2\lambda }|\mu |+\frac {1}{2}\left ( |\nabla h|^2+|h-1|^2\right ) \right )({{\Omega }})$
and
for every open set
![]() $U\subset {{\Omega }}$
. We can then apply Proposition 1.80 in [Reference Ambrosio, Fusco and Pallara4] to deduce that (3.1) holds. By using (3.4)-(3.5) and the strong convergence of
$U\subset {{\Omega }}$
. We can then apply Proposition 1.80 in [Reference Ambrosio, Fusco and Pallara4] to deduce that (3.1) holds. By using (3.4)-(3.5) and the strong convergence of
![]() $\frac {h_{\varepsilon }}{h_{\operatorname {\mathrm {\text {ex}}}}}$
in
$\frac {h_{\varepsilon }}{h_{\operatorname {\mathrm {\text {ex}}}}}$
in
![]() $L^2({{\Omega }})$
, we also arrive at (3.2) and (3.3).
$L^2({{\Omega }})$
, we also arrive at (3.2) and (3.3).
We are now ready to examine the convergence of the quadratic terms appearing in the formula for the second inner variation in Proposition 2.2.
Proposition 3.2 Let
![]() $ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of critical points of
$ \{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
be a family of critical points of
![]() $\mathrm {GL}_{\varepsilon }$
satisfying (1.8) and (1.9). Let us assume that (H) holds. Then, either the limiting vorticity is constant equal to
$\mathrm {GL}_{\varepsilon }$
satisfying (1.8) and (1.9). Let us assume that (H) holds. Then, either the limiting vorticity is constant equal to
![]() $1$
in all of
$1$
in all of
![]() ${{\Omega }}$
or, in the sense of measures,
${{\Omega }}$
or, in the sense of measures,
 $$ \begin{align*} \frac{|\partial_1^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_2h|^2+\frac{|\mu|}{2\lambda}, \quad \frac{|\partial_2^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_1h|^2+\frac{|\mu|}{2\lambda} \end{align*} $$
$$ \begin{align*} \frac{|\partial_1^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_2h|^2+\frac{|\mu|}{2\lambda}, \quad \frac{|\partial_2^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_1h|^2+\frac{|\mu|}{2\lambda} \end{align*} $$
 $$ \begin{align*} \frac{\langle \partial_1^{A_{\varepsilon}}u_{\varepsilon},\partial_2^{A_{\varepsilon}} u_{\varepsilon}\rangle }{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup -\partial_1h\partial_2h. \end{align*} $$
$$ \begin{align*} \frac{\langle \partial_1^{A_{\varepsilon}}u_{\varepsilon},\partial_2^{A_{\varepsilon}} u_{\varepsilon}\rangle }{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup -\partial_1h\partial_2h. \end{align*} $$
Proof Thanks to (1.8), the measures
![]() $\frac {|\partial _1^{A_{\varepsilon }}u_{\varepsilon }|^2}{h_{\operatorname {\mathrm {\text {ex}}}}^2}, \frac {|\partial _2^{A_{\varepsilon }}u_{\varepsilon }|^2}{h_{\operatorname {\mathrm {\text {ex}}}}^2} $
and
$\frac {|\partial _1^{A_{\varepsilon }}u_{\varepsilon }|^2}{h_{\operatorname {\mathrm {\text {ex}}}}^2}, \frac {|\partial _2^{A_{\varepsilon }}u_{\varepsilon }|^2}{h_{\operatorname {\mathrm {\text {ex}}}}^2} $
and
![]() $\frac {\langle \partial _1^{A_{\varepsilon }}u_{\varepsilon },\partial _2^{A_{\varepsilon }}u_{\varepsilon } \rangle }{h_{\operatorname {\mathrm {\text {ex}}}}^2} $
are bounded. Thus, there exist
$\frac {\langle \partial _1^{A_{\varepsilon }}u_{\varepsilon },\partial _2^{A_{\varepsilon }}u_{\varepsilon } \rangle }{h_{\operatorname {\mathrm {\text {ex}}}}^2} $
are bounded. Thus, there exist
![]() $\nu _1,\nu _2,\nu _3$
in
$\nu _1,\nu _2,\nu _3$
in
![]() ${\mathcal M}({{\Omega }})$
such that, in the sense of measures,
${\mathcal M}({{\Omega }})$
such that, in the sense of measures,
 $$ \begin{align*} \frac{|\partial_1^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_2h|^2+\nu_1, \quad \frac{|\partial_2^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_1h|^2+\nu_2, \quad \frac{\langle \partial_1^{A_{\varepsilon}}u_{\varepsilon},\partial_2^{A_{\varepsilon}} u_{\varepsilon}\rangle}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup -\partial_1h\partial_2h+\nu_3. \end{align*} $$
$$ \begin{align*} \frac{|\partial_1^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_2h|^2+\nu_1, \quad \frac{|\partial_2^{A_{\varepsilon}}u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_1h|^2+\nu_2, \quad \frac{\langle \partial_1^{A_{\varepsilon}}u_{\varepsilon},\partial_2^{A_{\varepsilon}} u_{\varepsilon}\rangle}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup -\partial_1h\partial_2h+\nu_3. \end{align*} $$
We use that from Corollary 2.6, we have that
![]() $\delta \mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon },\eta )=0$
for all
$\delta \mathrm {GL}_{\varepsilon }(u_{\varepsilon },A_{\varepsilon },\eta )=0$
for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, and this implies, thanks to the expressions in Proposition 2.2, that
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, and this implies, thanks to the expressions in Proposition 2.2, that
![]() $\frac {1}{h_{\operatorname {\mathrm {\text {ex}}}}^2}\mathrm {div} (T_{\varepsilon })=0$
in
$\frac {1}{h_{\operatorname {\mathrm {\text {ex}}}}^2}\mathrm {div} (T_{\varepsilon })=0$
in
![]() ${{\Omega }}$
, where
${{\Omega }}$
, where
![]() $T_{\varepsilon }$
is defined in (1.27). Then, by using (3.3), we pass to the limit when
$T_{\varepsilon }$
is defined in (1.27). Then, by using (3.3), we pass to the limit when
![]() ${\varepsilon } \to 0$
in the sense of distributions to find that
${\varepsilon } \to 0$
in the sense of distributions to find that
 $$ \begin{align} -\mathrm{div}(T_h)+\mathrm{div} \begin{pmatrix} \nu_1-\nu_2 & \nu_3 \\ \nu_3 & \nu_2-\nu_1 \end{pmatrix}=0, \end{align} $$
$$ \begin{align} -\mathrm{div}(T_h)+\mathrm{div} \begin{pmatrix} \nu_1-\nu_2 & \nu_3 \\ \nu_3 & \nu_2-\nu_1 \end{pmatrix}=0, \end{align} $$
where
![]() $(T_h)_{ij}= \partial _ih \partial _jh -\frac 12 (|\nabla h|^2+h^2)\delta _{ij}$
. But we can use Theorem 1.2 obtained in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32] to say that
$(T_h)_{ij}= \partial _ih \partial _jh -\frac 12 (|\nabla h|^2+h^2)\delta _{ij}$
. But we can use Theorem 1.2 obtained in [Reference Sandier and Serfaty31, Reference Sandier and Serfaty32] to say that
![]() $\mathrm {div} (T_h)=0$
and deduce that
$\mathrm {div} (T_h)=0$
and deduce that
 $\mathrm {div} \begin {pmatrix} \nu _1-\nu _2 & \nu _3 \\ \nu _3 & \nu _2-\nu _1 \end {pmatrix}=0$
. This equation can be rewritten as the Cauchy-Riemann system
$\mathrm {div} \begin {pmatrix} \nu _1-\nu _2 & \nu _3 \\ \nu _3 & \nu _2-\nu _1 \end {pmatrix}=0$
. This equation can be rewritten as the Cauchy-Riemann system
 $$ \begin{align*} \left\{ \begin{array}{@{}rcll} \partial_1(\nu_1-\nu_2)+\partial_2\nu_3 &=&0 \\ \partial_1 \nu_3 -\partial_2 (\nu_1-\nu_2) &=&0 \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{@{}rcll} \partial_1(\nu_1-\nu_2)+\partial_2\nu_3 &=&0 \\ \partial_1 \nu_3 -\partial_2 (\nu_1-\nu_2) &=&0 \end{array} \right. \end{align*} $$
or
![]() $\partial _{\bar {z}} (\nu _1-\nu _2-i\nu _3)=0$
, where
$\partial _{\bar {z}} (\nu _1-\nu _2-i\nu _3)=0$
, where
![]() $\partial _{\bar {z}}= \frac 12 (\partial _1+i\partial _2)$
. Since the operator
$\partial _{\bar {z}}= \frac 12 (\partial _1+i\partial _2)$
. Since the operator
![]() $\partial _{\bar {z}}$
is elliptic, we deduce that
$\partial _{\bar {z}}$
is elliptic, we deduce that
![]() $\nu _1-\nu _2-i\nu _3$
is holomorphic in
$\nu _1-\nu _2-i\nu _3$
is holomorphic in
![]() ${{\Omega }}$
. Now we can show that if
${{\Omega }}$
. Now we can show that if
![]() $\overline {{{\Omega }}}=\mathrm {supp\,} \mu $
, then h is constantly equal to
$\overline {{{\Omega }}}=\mathrm {supp\,} \mu $
, then h is constantly equal to
![]() $1$
. Indeed, by contradiction, if there exists
$1$
. Indeed, by contradiction, if there exists
![]() $x_0\in {{\Omega }}$
such that
$x_0\in {{\Omega }}$
such that
![]() $|\nabla h(x_0)|\neq 0$
, then from [Reference Rodiac27, Theorem 3.1]Footnote
4
there exists a neighbourhood
$|\nabla h(x_0)|\neq 0$
, then from [Reference Rodiac27, Theorem 3.1]Footnote
4
there exists a neighbourhood
![]() $\omega _{x_0}$
of
$\omega _{x_0}$
of
![]() $x_0$
in which we have
$x_0$
in which we have
![]() $\mu =\pm 2|\nabla h| \mathcal {H}^1_{\lfloor \mathrm {supp\,} \mu \cap \{ |\nabla h|>0\}}$
with
$\mu =\pm 2|\nabla h| \mathcal {H}^1_{\lfloor \mathrm {supp\,} \mu \cap \{ |\nabla h|>0\}}$
with
![]() $ \mathrm { supp\,} \mu \cap \{ |\nabla h|>0\}$
, which is a
$ \mathrm { supp\,} \mu \cap \{ |\nabla h|>0\}$
, which is a
![]() ${\mathcal C}^1$
curve. Hence, we find that
${\mathcal C}^1$
curve. Hence, we find that
![]() $|\mu |$
vanishes in a small ball included in
$|\mu |$
vanishes in a small ball included in
![]() $\omega _{x_0}$
and not intersecting this curve. This is a contradiction, and thus, we find that h is constant, and h being equal to
$\omega _{x_0}$
and not intersecting this curve. This is a contradiction, and thus, we find that h is constant, and h being equal to
![]() $1$
on
$1$
on
![]() $\partial {{\Omega }}$
, we conclude that
$\partial {{\Omega }}$
, we conclude that
![]() $h=1$
and
$h=1$
and
![]() $\mu =-\Delta h+h=1$
in
$\mu =-\Delta h+h=1$
in
![]() ${{\Omega }}$
.
${{\Omega }}$
.
Hence, if
![]() $h \neq 1$
, then
$h \neq 1$
, then
![]() $\mathrm {supp\,} \mu \neq \overline {{{\Omega }}}$
, and thus, there exists a ball
$\mathrm {supp\,} \mu \neq \overline {{{\Omega }}}$
, and thus, there exists a ball
![]() $B\subset {{\Omega }}$
such that
$B\subset {{\Omega }}$
such that
![]() ${|\mu |_{\lfloor B}=0}$
. We thus deduce from (3.2) that
${|\mu |_{\lfloor B}=0}$
. We thus deduce from (3.2) that
![]() $h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
converges strongly to h in B and
$h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
converges strongly to h in B and
![]() $\nu _1=\nu _2=0$
in B since
$\nu _1=\nu _2=0$
in B since
![]() $\nu _1+\nu _2=|\mu |/\lambda $
and
$\nu _1+\nu _2=|\mu |/\lambda $
and
![]() $\nu _1,\nu _2\geq 0$
.
$\nu _1,\nu _2\geq 0$
.
From (3.2), we also find that
![]() $\frac {|\nabla h_{\varepsilon }|^2}{h_{\operatorname {\mathrm {\text {ex}}}}^2|u_{\varepsilon }|^2}\rightharpoonup |\nabla h|^2$
in B. Since
$\frac {|\nabla h_{\varepsilon }|^2}{h_{\operatorname {\mathrm {\text {ex}}}}^2|u_{\varepsilon }|^2}\rightharpoonup |\nabla h|^2$
in B. Since
![]() $|\nabla h|^2 \mathrm {d} x$
does not charge the boundary
$|\nabla h|^2 \mathrm {d} x$
does not charge the boundary
![]() $\partial B$
from [Reference Evans and Gariepy15, Theorem 1.40], we deduce that
$\partial B$
from [Reference Evans and Gariepy15, Theorem 1.40], we deduce that
 $$\begin{align*}\int_B \frac{|\nabla h_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2|u_{\varepsilon}|^2} \rightarrow \int_B |\nabla h|^2.\end{align*}$$
$$\begin{align*}\int_B \frac{|\nabla h_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2|u_{\varepsilon}|^2} \rightarrow \int_B |\nabla h|^2.\end{align*}$$
Since
![]() $h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}} \rightarrow h $
in
$h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}} \rightarrow h $
in
![]() $H^1(B)$
, we can also assume that, up to a subsequence,
$H^1(B)$
, we can also assume that, up to a subsequence,
![]() $\nabla h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}} \rightarrow \nabla h$
a.e. in B. From the energy bound (1.8), we also know that
$\nabla h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}} \rightarrow \nabla h$
a.e. in B. From the energy bound (1.8), we also know that
![]() $ |u_{\varepsilon }|^2\rightarrow 1$
in
$ |u_{\varepsilon }|^2\rightarrow 1$
in
![]() $L^2({{\Omega }})$
, and hence, up to a subsequence,
$L^2({{\Omega }})$
, and hence, up to a subsequence,
![]() $|u_{\varepsilon }|\rightarrow 1$
a.e. Hence Brezis-Lieb’s lemma implies that
$|u_{\varepsilon }|\rightarrow 1$
a.e. Hence Brezis-Lieb’s lemma implies that
Now if we write, locally near a point where
![]() $u_{\varepsilon }$
does not vanish,
$u_{\varepsilon }$
does not vanish,
![]() $u_{\varepsilon }=\rho _{\varepsilon } e^{i\varphi _{\varepsilon }}$
, then
$u_{\varepsilon }=\rho _{\varepsilon } e^{i\varphi _{\varepsilon }}$
, then
and
Recalling that
![]() $-\nabla ^{\perp } h_{\varepsilon }= \rho _{\varepsilon }^2(\nabla \varphi _{\varepsilon }-A_{\varepsilon })$
, we arrive at
$-\nabla ^{\perp } h_{\varepsilon }= \rho _{\varepsilon }^2(\nabla \varphi _{\varepsilon }-A_{\varepsilon })$
, we arrive at
We use (3.3) to infer that
![]() $ \rho _{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}} \rightarrow 0$
strongly in
$ \rho _{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}} \rightarrow 0$
strongly in
![]() $H^1({{\Omega }})$
, and then we use this together with (3.12) to find that
$H^1({{\Omega }})$
, and then we use this together with (3.12) to find that
![]() $\frac {1}{h_{\operatorname {\mathrm {\text {ex}}}}^2}\langle \partial _1^{A_{\varepsilon }} u_{\varepsilon }, \partial _2^{A_{\varepsilon }} u_{\varepsilon } \rangle \rightarrow -\partial _2h \partial _1h$
in
$\frac {1}{h_{\operatorname {\mathrm {\text {ex}}}}^2}\langle \partial _1^{A_{\varepsilon }} u_{\varepsilon }, \partial _2^{A_{\varepsilon }} u_{\varepsilon } \rangle \rightarrow -\partial _2h \partial _1h$
in
![]() $L^1(B)$
. This implies that
$L^1(B)$
. This implies that
![]() $\nu _3=0$
in B.
$\nu _3=0$
in B.
We have thus obtained that
![]() $\nu _1-\nu _2-i\nu _3$
vanishes in the ball B. This quantity being holomorphic, the principle of isolated zeros implies that
$\nu _1-\nu _2-i\nu _3$
vanishes in the ball B. This quantity being holomorphic, the principle of isolated zeros implies that
![]() $\nu _1=\nu _2$
and
$\nu _1=\nu _2$
and
![]() $\nu _3=0$
everywhere in
$\nu _3=0$
everywhere in
![]() ${{\Omega }}$
. Since
${{\Omega }}$
. Since
![]() $\nu _1+\nu _2= |\mu |/\lambda $
, we find that
$\nu _1+\nu _2= |\mu |/\lambda $
, we find that
![]() $\nu _1=\nu _2=\frac {|\mu |}{2\lambda }$
and
$\nu _1=\nu _2=\frac {|\mu |}{2\lambda }$
and
![]() $\nu _3=0$
.
$\nu _3=0$
.
3.2 The case without magnetic field
In this section, we state the analogue of Proposition 3.1 and 3.2 in the case of the GL energy without magnetic field. Since the proofs require only minor adaptations of the previous paragraph, they are left to the reader.
Proposition 3.3 Let
![]() $ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
be a family of critical points of
$ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
be a family of critical points of
![]() $E_{\varepsilon }$
satisfying (1.21). We set
$E_{\varepsilon }$
satisfying (1.21). We set
![]() $\tilde {j}_{\varepsilon }=\langle iu_{\varepsilon },\nabla u_{\varepsilon }\rangle $
and
$\tilde {j}_{\varepsilon }=\langle iu_{\varepsilon },\nabla u_{\varepsilon }\rangle $
and
![]() $U_{\varepsilon }\in H^1({{\Omega }})$
the unique function such that
$U_{\varepsilon }\in H^1({{\Omega }})$
the unique function such that
![]() $\nabla ^{\perp } U_{\varepsilon }=\tilde {j}_{\varepsilon }$
and
$\nabla ^{\perp } U_{\varepsilon }=\tilde {j}_{\varepsilon }$
and
![]() ${\int _{{\Omega }} U_{\varepsilon } =0}$
.
${\int _{{\Omega }} U_{\varepsilon } =0}$
.
-
1) Up to a subsequence,
(3.13) $$ \begin{align} \frac{\mu(u_{\varepsilon})}{|\log {\varepsilon}|}:=\frac{\mathrm{curl\,} \tilde{j}_{\varepsilon}}{|\log {\varepsilon}|} \xrightarrow[{\varepsilon} \to 0]{} \mu \quad \text{ in } \left( {\mathcal C}^{0,\gamma}({{\Omega}})\right)^* \end{align} $$
$$ \begin{align} \frac{\mu(u_{\varepsilon})}{|\log {\varepsilon}|}:=\frac{\mathrm{curl\,} \tilde{j}_{\varepsilon}}{|\log {\varepsilon}|} \xrightarrow[{\varepsilon} \to 0]{} \mu \quad \text{ in } \left( {\mathcal C}^{0,\gamma}({{\Omega}})\right)^* \end{align} $$
for every
 $\gamma \in (0,1)$
and (3.14)
$\gamma \in (0,1)$
and (3.14)
with
 $-\nabla ^{\perp } U=\tilde {j}$
and
$-\nabla ^{\perp } U=\tilde {j}$
and
 $\mu =-\Delta U$
. Furthermore, (3.15)
$\mu =-\Delta U$
. Furthermore, (3.15) $$ \begin{align} \liminf_{{\varepsilon} \to 0} \frac{E_{\varepsilon}(u_{\varepsilon})}{|\log {\varepsilon}|^2}\geq \frac{|\mu|({{\Omega}})}{2}+\frac12 \int_{{\Omega}} |\nabla U|^2. \end{align} $$
$$ \begin{align} \liminf_{{\varepsilon} \to 0} \frac{E_{\varepsilon}(u_{\varepsilon})}{|\log {\varepsilon}|^2}\geq \frac{|\mu|({{\Omega}})}{2}+\frac12 \int_{{\Omega}} |\nabla U|^2. \end{align} $$
-
2) Let us assume that (H') holds. Then, if we set
 $e_{\varepsilon }(u):=\frac 12 \left (|\nabla u|^2+\frac {1}{2{\varepsilon }^2}(1-|u|^2)^2 \right )$
, then (3.16)
$e_{\varepsilon }(u):=\frac 12 \left (|\nabla u|^2+\frac {1}{2{\varepsilon }^2}(1-|u|^2)^2 \right )$
, then (3.16) $$ \begin{align} \frac{e_{\varepsilon}(u_{\varepsilon})}{|\log {\varepsilon}|^2} \rightharpoonup \frac{1}{2}|\mu|+\frac{1}{2}\left( |\nabla U|^2\right) \text{ in } {\mathcal M}({{\Omega}}), \end{align} $$
$$ \begin{align} \frac{e_{\varepsilon}(u_{\varepsilon})}{|\log {\varepsilon}|^2} \rightharpoonup \frac{1}{2}|\mu|+\frac{1}{2}\left( |\nabla U|^2\right) \text{ in } {\mathcal M}({{\Omega}}), \end{align} $$
 $\frac {|\nabla U_{\varepsilon }|^2}{|\log {\varepsilon }|^2}\rightharpoonup |\nabla U|^2+|\mu | \text { in } {\mathcal M}({{\Omega }})$
and
$\frac {|\nabla U_{\varepsilon }|^2}{|\log {\varepsilon }|^2}\rightharpoonup |\nabla U|^2+|\mu | \text { in } {\mathcal M}({{\Omega }})$
and
 $\frac {|\nabla U_{\varepsilon }|^2}{|u_{\varepsilon }|^2|\log {\varepsilon }|^2}\rightharpoonup |\nabla U|^2+|\mu | \text { in } {\mathcal M}({{\Omega }})$
.
$\frac {|\nabla U_{\varepsilon }|^2}{|u_{\varepsilon }|^2|\log {\varepsilon }|^2}\rightharpoonup |\nabla U|^2+|\mu | \text { in } {\mathcal M}({{\Omega }})$
.
Proposition 3.4 Let
![]() $ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
be a family of critical points of
$ \{u_{\varepsilon }\}_{{\varepsilon }>0}$
be a family of critical points of
![]() $E_{\varepsilon }$
. Let us assume that (H') holds, then, in the sense of measures,
$E_{\varepsilon }$
. Let us assume that (H') holds, then, in the sense of measures,
 $$ \begin{align} \frac{|\partial_1u_{\varepsilon}|^2}{|\log {\varepsilon}|^2} \rightharpoonup |\partial_2U|^2+\frac{|\mu|}{2}, \quad \frac{|\partial_2u_{\varepsilon}|^2}{|\log {\varepsilon}|^2} \rightharpoonup |\partial_1U|^2+\frac{|\mu|}{2} \end{align} $$
$$ \begin{align} \frac{|\partial_1u_{\varepsilon}|^2}{|\log {\varepsilon}|^2} \rightharpoonup |\partial_2U|^2+\frac{|\mu|}{2}, \quad \frac{|\partial_2u_{\varepsilon}|^2}{|\log {\varepsilon}|^2} \rightharpoonup |\partial_1U|^2+\frac{|\mu|}{2} \end{align} $$
 $$ \begin{align} \frac{\langle \partial_1u_{\varepsilon},\partial_2 u_{\varepsilon} \rangle}{|\log {\varepsilon}|^2} \rightharpoonup -\partial_1U \partial_2U. \end{align} $$
$$ \begin{align} \frac{\langle \partial_1u_{\varepsilon},\partial_2 u_{\varepsilon} \rangle}{|\log {\varepsilon}|^2} \rightharpoonup -\partial_1U \partial_2U. \end{align} $$
Proof The proof follows the same lines as the proof of Proposition 3.2. However, we use [Reference Rodiac26, Theorem 1.3]Footnote
5
to say that
![]() $\mu $
is locally supported on a union of curves instead of the results in [Reference Rodiac27, Theorem 3.1].
$\mu $
is locally supported on a union of curves instead of the results in [Reference Rodiac27, Theorem 3.1].
3.3 Proofs of the main theorems
We are now ready to prove Theorem 1.3.
Proof of Theorem 1.3
Let
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
. We want to understand the limit of
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
. We want to understand the limit of
 $$ \begin{align*} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2}&=\frac{1}{h_{\operatorname{\mathrm{\text{ex}}}}^2}\int_{{\Omega}} \Big(|(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta|^2-|\mathrm{D} u-u^{\perp} A^T|^2 \det \mathrm{D} \eta \\ & \quad +h^2 \left[ (\mathrm{div} \eta)^2-\det \mathrm{D} \eta \right] +\frac{1}{{\varepsilon}^2}(1-|u|^2)^2 \det \mathrm{D} \eta \Big). \end{align*} $$
$$ \begin{align*} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2}&=\frac{1}{h_{\operatorname{\mathrm{\text{ex}}}}^2}\int_{{\Omega}} \Big(|(\mathrm{D} u-u^{\perp} A^T)\mathrm{D} \eta|^2-|\mathrm{D} u-u^{\perp} A^T|^2 \det \mathrm{D} \eta \\ & \quad +h^2 \left[ (\mathrm{div} \eta)^2-\det \mathrm{D} \eta \right] +\frac{1}{{\varepsilon}^2}(1-|u|^2)^2 \det \mathrm{D} \eta \Big). \end{align*} $$
We note that
Now, since
![]() $|\nabla _A u|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2$
and
$|\nabla _A u|^2/h_{\operatorname {\mathrm {\text {ex}}}}^2$
and
![]() $(1-|u|^2)^2/h_{\operatorname {\mathrm {\text {ex}}}}^2$
are bounded sequences in
$(1-|u|^2)^2/h_{\operatorname {\mathrm {\text {ex}}}}^2$
are bounded sequences in
![]() $L^1({{\Omega }})$
, we can extract subsequences for which we have the following convergence in the sense of measures:
$L^1({{\Omega }})$
, we can extract subsequences for which we have the following convergence in the sense of measures:
 $$ \begin{align*} \frac{|\partial_1^{A_{\varepsilon}} u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_2h|^2 +\nu_1, \quad \frac{|\partial_2^{A_{\varepsilon}} u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2}\rightharpoonup |\partial_1h|^2 +\nu_2, \\ \frac{\langle \partial_1^{A_{\varepsilon}}u_{\varepsilon},\partial_2^{A_{\varepsilon}}u_{\varepsilon}\rangle }{h_{\operatorname{\mathrm{\text{ex}}}}^2}\rightharpoonup -\partial_1h \partial_2h+\nu_3, \quad \frac{(1-|u|^2)^2}{{\varepsilon}^2 h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup \nu_4, \end{align*} $$
$$ \begin{align*} \frac{|\partial_1^{A_{\varepsilon}} u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup |\partial_2h|^2 +\nu_1, \quad \frac{|\partial_2^{A_{\varepsilon}} u_{\varepsilon}|^2}{h_{\operatorname{\mathrm{\text{ex}}}}^2}\rightharpoonup |\partial_1h|^2 +\nu_2, \\ \frac{\langle \partial_1^{A_{\varepsilon}}u_{\varepsilon},\partial_2^{A_{\varepsilon}}u_{\varepsilon}\rangle }{h_{\operatorname{\mathrm{\text{ex}}}}^2}\rightharpoonup -\partial_1h \partial_2h+\nu_3, \quad \frac{(1-|u|^2)^2}{{\varepsilon}^2 h_{\operatorname{\mathrm{\text{ex}}}}^2} \rightharpoonup \nu_4, \end{align*} $$
with
![]() $\nu _1,\nu _2,\nu _3,\nu _4 \in \mathcal {M}({{\Omega }})$
. By using that
$\nu _1,\nu _2,\nu _3,\nu _4 \in \mathcal {M}({{\Omega }})$
. By using that
![]() $h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
is bounded in
$h_{\varepsilon }/h_{\operatorname {\mathrm {\text {ex}}}}$
is bounded in
![]() $H^1({{\Omega }})$
, we also have that, up to a subsequence
$H^1({{\Omega }})$
, we also have that, up to a subsequence
![]() $h_{\varepsilon } \rightarrow h$
strongly in
$h_{\varepsilon } \rightarrow h$
strongly in
![]() $L^2({{\Omega }})$
. Thus, we can pass to the limit and we find that
$L^2({{\Omega }})$
. Thus, we can pass to the limit and we find that
 $$ \begin{align*} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &\xrightarrow[{\varepsilon} \to 0]{} \int_{{\Omega}} \Big[ (|\partial_2 h|^2+\nu_1) |\nabla \eta_1|^2+(|\partial_1h|^2|+\nu_2) |\nabla \eta_2|^2\\ & -(2\partial_1h\partial_2h-2\nu_3) \nabla \eta_1\cdot \nabla \eta_2 \\ &+(|\nabla h|^2+\nu_1+\nu_2) \det \mathrm{D} \eta+h^2\left[(\mathrm{div} \eta)^2-\det \mathrm{D} \eta \right]+ \nu_4 \det \mathrm{D} \eta \Big]. \end{align*} $$
$$ \begin{align*} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &\xrightarrow[{\varepsilon} \to 0]{} \int_{{\Omega}} \Big[ (|\partial_2 h|^2+\nu_1) |\nabla \eta_1|^2+(|\partial_1h|^2|+\nu_2) |\nabla \eta_2|^2\\ & -(2\partial_1h\partial_2h-2\nu_3) \nabla \eta_1\cdot \nabla \eta_2 \\ &+(|\nabla h|^2+\nu_1+\nu_2) \det \mathrm{D} \eta+h^2\left[(\mathrm{div} \eta)^2-\det \mathrm{D} \eta \right]+ \nu_4 \det \mathrm{D} \eta \Big]. \end{align*} $$
Now, if we assume the convergence of energy (H), then (3.3) and Proposition 3.2 give that
![]() $\nu _1=\nu _2=|\mu |/2\lambda $
,
$\nu _1=\nu _2=|\mu |/2\lambda $
,
![]() $\nu _3=0$
and
$\nu _3=0$
and
![]() $\nu _4=0$
. This allows us to rewrite
$\nu _4=0$
. This allows us to rewrite
 $$ \begin{align*} \lim_{{\varepsilon} \to 0} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &= \int_{{\Omega}} \Big( |\partial_2 h|^2 |\nabla \eta_1|^2+|\partial_1h|^2| \nabla \eta_2|^2-2\partial_1h\partial_2h \nabla \eta_1\cdot \nabla \eta_2 \\ & +|\nabla h|^2 \det \mathrm{D} \eta +h^2\left[(\mathrm{div} \eta)^2-\det \mathrm{D} \eta \right]\Big)+\int_{{\Omega}} \left( \frac{|\mathrm{D} \eta|^2}{2}- \det \mathrm{D} \eta \right) \frac{\mathrm{d}|\mu|}{\lambda}. \end{align*} $$
$$ \begin{align*} \lim_{{\varepsilon} \to 0} \frac{\delta^2 \mathrm{GL}_{\varepsilon}(u_{\varepsilon},A_{\varepsilon},\eta)}{h_{\operatorname{\mathrm{\text{ex}}}}^2} &= \int_{{\Omega}} \Big( |\partial_2 h|^2 |\nabla \eta_1|^2+|\partial_1h|^2| \nabla \eta_2|^2-2\partial_1h\partial_2h \nabla \eta_1\cdot \nabla \eta_2 \\ & +|\nabla h|^2 \det \mathrm{D} \eta +h^2\left[(\mathrm{div} \eta)^2-\det \mathrm{D} \eta \right]\Big)+\int_{{\Omega}} \left( \frac{|\mathrm{D} \eta|^2}{2}- \det \mathrm{D} \eta \right) \frac{\mathrm{d}|\mu|}{\lambda}. \end{align*} $$
We can conclude since
![]() $ |\mathrm {D} \eta ^T \nabla ^{\perp } h|^2= |\partial _2 h|^2 |\nabla \eta _1|^2+|\partial _1h|^2| \nabla \eta _2|^2-2\partial _1h\partial _2h \nabla \eta _1\cdot \nabla \eta _2$
. To finish the proof, we need to show the validity of (1.17). This is a consequence of the link between inner and outer variations cf. Corollary 2.6, the definition of stability, and the limit of the second inner variation previously obtained.
$ |\mathrm {D} \eta ^T \nabla ^{\perp } h|^2= |\partial _2 h|^2 |\nabla \eta _1|^2+|\partial _1h|^2| \nabla \eta _2|^2-2\partial _1h\partial _2h \nabla \eta _1\cdot \nabla \eta _2$
. To finish the proof, we need to show the validity of (1.17). This is a consequence of the link between inner and outer variations cf. Corollary 2.6, the definition of stability, and the limit of the second inner variation previously obtained.
The proof of Theorem 1.4 follows the same lines by using Proposition 3.4 and is left to the reader.
4 Analyzing the limiting stability condition
As a consequence of Corollary 2.6 and Theorem 1.3, we can see that if
![]() $\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
is a family of stable critical points of
$\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
is a family of stable critical points of
![]() $\mathrm {GL}_{\varepsilon }$
, then
$\mathrm {GL}_{\varepsilon }$
, then
![]() $Q_h(\eta )\geq 0$
for every
$Q_h(\eta )\geq 0$
for every
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, with
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, with
![]() $Q_h$
defined in (1.16). We would like to analyze if this limiting stability condition implies more regularity on the limiting vorticity. In the case with magnetic field, we take a specific example of an admissible limiting vorticity supported on a line in the Lipschitz bounded domainFootnote
6
$Q_h$
defined in (1.16). We would like to analyze if this limiting stability condition implies more regularity on the limiting vorticity. In the case with magnetic field, we take a specific example of an admissible limiting vorticity supported on a line in the Lipschitz bounded domainFootnote
6
![]() ${{\Omega }}=(-L,L)^2$
, and we show that the associated limiting magnetic field h satisfies that
${{\Omega }}=(-L,L)^2$
, and we show that the associated limiting magnetic field h satisfies that
![]() $Q_h(\eta )\geq 0$
for every
$Q_h(\eta )\geq 0$
for every
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
if
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
if
![]() $L>0$
is small enough, whereas there exists
$L>0$
is small enough, whereas there exists
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
such that
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
such that
![]() $Q_h(\eta )<0$
for L large enough. This shows that the link between limiting stability of the vorticity measure and regularity might be subtle and may depend on other factors such as the size of the domain. In the case without magnetic field, the situation is even worse in a sense. Indeed, we can use a result of Iwaniec-Onninen [Reference Iwaniec and Onninen18] to prove that every limiting vorticity measure satisfies that
$Q_h(\eta )<0$
for L large enough. This shows that the link between limiting stability of the vorticity measure and regularity might be subtle and may depend on other factors such as the size of the domain. In the case without magnetic field, the situation is even worse in a sense. Indeed, we can use a result of Iwaniec-Onninen [Reference Iwaniec and Onninen18] to prove that every limiting vorticity measure satisfies that
![]() $\tilde {Q}_U(\eta )\geq 0$
for every
$\tilde {Q}_U(\eta )\geq 0$
for every
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, where
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, where
![]() $\tilde {Q}_U$
is defined in (1.26). This shows that no supplementary regularity can be obtained from our limiting stability condition in that case.
$\tilde {Q}_U$
is defined in (1.26). This shows that no supplementary regularity can be obtained from our limiting stability condition in that case.
4.1 The case with magnetic field
Proposition 4.1 Let
![]() ${{\Omega }}=(-L,L)^2$
. We set
${{\Omega }}=(-L,L)^2$
. We set
![]() $h(x,y)=e^{-|x|}$
for
$h(x,y)=e^{-|x|}$
for
![]() $ (x,y)\in {{\Omega }}$
. Then h satisfies
$ (x,y)\in {{\Omega }}$
. Then h satisfies
![]() $-\Delta h+h=\mu $
in
$-\Delta h+h=\mu $
in
![]() ${{\Omega }}$
with
${{\Omega }}$
with
![]() $\mu =-2\mathcal {H}^1_{\lfloor \{x=0\}}$
, and h satisfies (1.10). With
$\mu =-2\mathcal {H}^1_{\lfloor \{x=0\}}$
, and h satisfies (1.10). With
![]() $Q_h$
defined in (1.16), we have that
$Q_h$
defined in (1.16), we have that
-
1) if
 $L>0$
is small enough, then
$L>0$
is small enough, then
 $Q_h(\eta )\geq 0$
for all
$Q_h(\eta )\geq 0$
for all
 $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
, -
2) if
 $L>0$
is large enough, then
$L>0$
is large enough, then
 $Q_h(\eta )<0$
for
$Q_h(\eta )<0$
for
 $\eta =(\cos \frac {\pi x}{2L} \sin \frac {\pi y}{2L}, -\sin \frac {\pi x}{2L}\cos \frac {\pi y}{2L})^T$
.
$\eta =(\cos \frac {\pi x}{2L} \sin \frac {\pi y}{2L}, -\sin \frac {\pi x}{2L}\cos \frac {\pi y}{2L})^T$
.
Proof We can check by direct computation that
![]() $-\Delta h+h=-2\mathcal {H}^1_{\lfloor \{x=0\}}$
since the 1D function satisfies
$-\Delta h+h=-2\mathcal {H}^1_{\lfloor \{x=0\}}$
since the 1D function satisfies
![]() $-h"+h=-2\delta _{x=0}$
. Besides, the condition (1.10) is equivalent to
$-h"+h=-2\delta _{x=0}$
. Besides, the condition (1.10) is equivalent to
![]() $ (|h'|^2-h^2)'=0$
in
$ (|h'|^2-h^2)'=0$
in
![]() $(-L,L)$
since h is a function of one variable. But we have that
$(-L,L)$
since h is a function of one variable. But we have that
![]() $|h'|^2=|h|^2$
so (1.10) is satisfied. We now consider the stability/instability properties.
$|h'|^2=|h|^2$
so (1.10) is satisfied. We now consider the stability/instability properties.
-
1) We first observe that
(4.1)Hence, $$ \begin{align} |\det \mathrm{D} \eta|&=|\partial_1 \eta \wedge \partial_2\eta |\leq |\partial_1 \eta||\partial_2\eta| \leq \frac12 (|\partial_1 \eta|^2+|\partial_2 \eta|^2)=\frac{|\mathrm{D} \eta|^2}{2}. \end{align} $$
Then we show the following Poincaré type inequality: for every
$$ \begin{align} |\det \mathrm{D} \eta|&=|\partial_1 \eta \wedge \partial_2\eta |\leq |\partial_1 \eta||\partial_2\eta| \leq \frac12 (|\partial_1 \eta|^2+|\partial_2 \eta|^2)=\frac{|\mathrm{D} \eta|^2}{2}. \end{align} $$
Then we show the following Poincaré type inequality: for every $$ \begin{align*} Q_h(\eta)&\geq \int_{{\Omega}} \left[|\mathrm{D} \eta^T\nabla^{\perp} h|^2- (|\nabla h|^2+h^2)\det \mathrm{D} \eta+h^2(\mathrm{div}\ \eta)^2 \right] \\ &\geq \int_{{\Omega}} \left[ |h'|^2|\nabla \eta_2|^2-(|h'|^2+h^2)\det \mathrm{D} \eta+h^2 (\mathrm{div}\ \eta)^2 \right]. \end{align*} $$
$$ \begin{align*} Q_h(\eta)&\geq \int_{{\Omega}} \left[|\mathrm{D} \eta^T\nabla^{\perp} h|^2- (|\nabla h|^2+h^2)\det \mathrm{D} \eta+h^2(\mathrm{div}\ \eta)^2 \right] \\ &\geq \int_{{\Omega}} \left[ |h'|^2|\nabla \eta_2|^2-(|h'|^2+h^2)\det \mathrm{D} \eta+h^2 (\mathrm{div}\ \eta)^2 \right]. \end{align*} $$
 $\eta _1\in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R})$
, (4.2)Indeed, we write
$\eta _1\in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R})$
, (4.2)Indeed, we write $$ \begin{align} \int_{(-L,L)^2} e^{-2|x|}|\eta_1(x,y)|^2 \mathrm{d} x \mathrm{d} y \leq 2L(e^{2L}-1) \int_{ (-L,L)^2} e^{-2|x|} |\partial_1 \eta_1(x,y)|^2 \mathrm{d} x \mathrm{d} y. \end{align} $$
We notice that, since
$$ \begin{align} \int_{(-L,L)^2} e^{-2|x|}|\eta_1(x,y)|^2 \mathrm{d} x \mathrm{d} y \leq 2L(e^{2L}-1) \int_{ (-L,L)^2} e^{-2|x|} |\partial_1 \eta_1(x,y)|^2 \mathrm{d} x \mathrm{d} y. \end{align} $$
We notice that, since $$ \begin{align*} \int_{(-L,L)^2} h^2 |\eta_1|^2 &=\int_{ (-L,L)^2} h^2(x)\left( \int_{-L}^x \partial_1\eta_1(s,y) \mathrm{d} s \right)^2 \mathrm{d} x \mathrm{d} y \\ &\leq \int_{ (-L,L)^2} h^2(x) \int_{-L}^x|\partial_1\eta_1(s,y)|^2 \mathrm{d} s (x+L) \mathrm{d} x \mathrm{d} y \\ &\leq 2L \int_{-L}^L h^2(x) \mathrm{d} x \int_{(-L,L)^2} |\partial_1\eta_1(s,y)|^2 \mathrm{d} s \mathrm{d} y \\ &\leq 2L\int_{-L}^L h^2(x) \mathrm{d} x \times e^{2L} \times \int_{(-L,L)^2} e^{-2|s|}|\partial_1\eta_1(s,y)|^2 \mathrm{d} s \mathrm{d} y \\ &\leq 2L (1-e^{-2L})e^{2L} \int_{(-L,L)^2} e^{-2|s|}|\partial_1\eta_1(s,y)|^2 \mathrm{d} s \mathrm{d} y. \end{align*} $$
$$ \begin{align*} \int_{(-L,L)^2} h^2 |\eta_1|^2 &=\int_{ (-L,L)^2} h^2(x)\left( \int_{-L}^x \partial_1\eta_1(s,y) \mathrm{d} s \right)^2 \mathrm{d} x \mathrm{d} y \\ &\leq \int_{ (-L,L)^2} h^2(x) \int_{-L}^x|\partial_1\eta_1(s,y)|^2 \mathrm{d} s (x+L) \mathrm{d} x \mathrm{d} y \\ &\leq 2L \int_{-L}^L h^2(x) \mathrm{d} x \int_{(-L,L)^2} |\partial_1\eta_1(s,y)|^2 \mathrm{d} s \mathrm{d} y \\ &\leq 2L\int_{-L}^L h^2(x) \mathrm{d} x \times e^{2L} \times \int_{(-L,L)^2} e^{-2|s|}|\partial_1\eta_1(s,y)|^2 \mathrm{d} s \mathrm{d} y \\ &\leq 2L (1-e^{-2L})e^{2L} \int_{(-L,L)^2} e^{-2|s|}|\partial_1\eta_1(s,y)|^2 \mathrm{d} s \mathrm{d} y. \end{align*} $$
 $ |h'|^2=h^2=e^{-2|x|}$
, By using successively two Young’s inequalities, by observing that
$ |h'|^2=h^2=e^{-2|x|}$
, By using successively two Young’s inequalities, by observing that $$ \begin{align*} \int_{{\Omega}} \left( |h'|^2+h^2\right) \det \mathrm{D} \eta &= \frac12 \int_{{\Omega}} \left( |h'|^2+h^2\right) \mathrm{div} (\eta \wedge \partial_2\eta, \partial_1 \eta \wedge \eta) \\ &=-\frac12 \int_{{\Omega}} \left( |h'|^2+h^2\right)' \eta \wedge \partial_2 \eta =-\int (h^2)'(\eta_1\partial_2\eta_2-\eta_2\partial_2\eta_1) \\ &=-2\int_{{\Omega}} (h^2)'\eta_1\partial_2\eta_2=-4\int_{{\Omega}} h h' \eta_1\partial_2\eta_2. \end{align*} $$
$$ \begin{align*} \int_{{\Omega}} \left( |h'|^2+h^2\right) \det \mathrm{D} \eta &= \frac12 \int_{{\Omega}} \left( |h'|^2+h^2\right) \mathrm{div} (\eta \wedge \partial_2\eta, \partial_1 \eta \wedge \eta) \\ &=-\frac12 \int_{{\Omega}} \left( |h'|^2+h^2\right)' \eta \wedge \partial_2 \eta =-\int (h^2)'(\eta_1\partial_2\eta_2-\eta_2\partial_2\eta_1) \\ &=-2\int_{{\Omega}} (h^2)'\eta_1\partial_2\eta_2=-4\int_{{\Omega}} h h' \eta_1\partial_2\eta_2. \end{align*} $$
 $ |h'|^2=|h^2|=e^{-2|x|}$
, and by employing the former Poincaré’s inequality (4.2), we find that Now we choose first
$ |h'|^2=|h^2|=e^{-2|x|}$
, and by employing the former Poincaré’s inequality (4.2), we find that Now we choose first $$ \begin{align*} Q_h(\eta) &\geq \int_{{\Omega}} |h'|^2 |\nabla \eta_2|^2+4hh'\eta_1\partial_2\eta_2+h^2(\partial_1\eta_1+\partial_2\eta_2)^2 \\ & \geq \int_{{{\Omega}}} |h'|^2 |\nabla \eta_2|^2-2\alpha^2h^2 |\eta_1|^2-2|h'|^2\frac{|\partial_2\eta_2|^2}{\alpha^2} \\ & \quad +h^2 (|\partial_1\eta_1|^2+|\partial_2 \eta_2|^2-\beta^2|\partial_1\eta_1|^2-\frac{|\partial_2 \eta_2|^2}{\beta^2} \\ & \geq \int_{{\Omega}} |h'|^2 \Big[ |\partial_2\eta_2|^2(2-\frac{2}{\alpha^2}-\frac{1}{\beta^2})+|\partial_1 \eta_2|^2 \\ & \quad +|\partial_1\eta_1|^2\left(1-\beta^2-4\alpha^2L(e^{2L}-1) \right)\Big]. \end{align*} $$
$$ \begin{align*} Q_h(\eta) &\geq \int_{{\Omega}} |h'|^2 |\nabla \eta_2|^2+4hh'\eta_1\partial_2\eta_2+h^2(\partial_1\eta_1+\partial_2\eta_2)^2 \\ & \geq \int_{{{\Omega}}} |h'|^2 |\nabla \eta_2|^2-2\alpha^2h^2 |\eta_1|^2-2|h'|^2\frac{|\partial_2\eta_2|^2}{\alpha^2} \\ & \quad +h^2 (|\partial_1\eta_1|^2+|\partial_2 \eta_2|^2-\beta^2|\partial_1\eta_1|^2-\frac{|\partial_2 \eta_2|^2}{\beta^2} \\ & \geq \int_{{\Omega}} |h'|^2 \Big[ |\partial_2\eta_2|^2(2-\frac{2}{\alpha^2}-\frac{1}{\beta^2})+|\partial_1 \eta_2|^2 \\ & \quad +|\partial_1\eta_1|^2\left(1-\beta^2-4\alpha^2L(e^{2L}-1) \right)\Big]. \end{align*} $$
 $\beta $
so that
$\beta $
so that
 $1-\beta ^2>0$
and
$1-\beta ^2>0$
and
 $2-\frac {1}{\beta ^2}>0$
. This amounts to take
$2-\frac {1}{\beta ^2}>0$
. This amounts to take
 $ 1/\sqrt {2}<\beta <1$
. Then we choose
$ 1/\sqrt {2}<\beta <1$
. Then we choose
 $\alpha $
big enough so that
$\alpha $
big enough so that
 $ 2-\frac {2}{\alpha ^2}-\frac {1}{\beta ^2}>0$
, and it remains to adjust L to have
$ 2-\frac {2}{\alpha ^2}-\frac {1}{\beta ^2}>0$
, and it remains to adjust L to have
 $1-\beta ^2-4\alpha ^2L(e^{2L}-1)>0$
. Thus. the first point is proved.
$1-\beta ^2-4\alpha ^2L(e^{2L}-1)>0$
. Thus. the first point is proved.
-
2) Let
 $\eta =(\cos \frac {\pi x}{2L} \sin \frac {\pi y}{2L}, -\sin \frac {\pi x}{2L}\cos \frac {\pi y}{2L})^T$
. We can compute that Thus,
$\eta =(\cos \frac {\pi x}{2L} \sin \frac {\pi y}{2L}, -\sin \frac {\pi x}{2L}\cos \frac {\pi y}{2L})^T$
. We can compute that Thus, $$\begin{align*}\mathrm{D} \eta =\frac{\pi}{2L}\begin{pmatrix} -\sin \frac{\pi x}{2L}\sin \frac{\pi y}{2L} & \cos \frac{\pi x}{2L}\cos \frac{\pi y}{2L} \\ -\cos \frac{\pi x}{2L}\cos \frac{\pi y}{2L} & \sin \frac{\pi x}{2L}\sin \frac{\pi y}{2L}. \end{pmatrix}\end{align*}$$
$$\begin{align*}\mathrm{D} \eta =\frac{\pi}{2L}\begin{pmatrix} -\sin \frac{\pi x}{2L}\sin \frac{\pi y}{2L} & \cos \frac{\pi x}{2L}\cos \frac{\pi y}{2L} \\ -\cos \frac{\pi x}{2L}\cos \frac{\pi y}{2L} & \sin \frac{\pi x}{2L}\sin \frac{\pi y}{2L}. \end{pmatrix}\end{align*}$$
 $ \frac {|\mathrm {D} \eta |^2}{2}=\frac {\pi ^2}{4L^2}(\sin ^2 \frac {\pi x}{2L}\sin ^2 \frac {\pi y}{2L}+\cos ^2 \frac {\pi x}{2L}\cos ^2 \frac {\pi y}{2L})$
and
$ \frac {|\mathrm {D} \eta |^2}{2}=\frac {\pi ^2}{4L^2}(\sin ^2 \frac {\pi x}{2L}\sin ^2 \frac {\pi y}{2L}+\cos ^2 \frac {\pi x}{2L}\cos ^2 \frac {\pi y}{2L})$
and
 $\det \mathrm {D} \eta = \frac {\pi ^2}{4L}(-\sin ^2 \frac {\pi x}{2L}\sin ^2 \frac {\pi y}{2l}+\cos ^2 \frac {\pi x}{2L}\cos ^2 \frac {\pi y}{2L})$
. Thus, we see that However, direct computations show that
$\det \mathrm {D} \eta = \frac {\pi ^2}{4L}(-\sin ^2 \frac {\pi x}{2L}\sin ^2 \frac {\pi y}{2l}+\cos ^2 \frac {\pi x}{2L}\cos ^2 \frac {\pi y}{2L})$
. Thus, we see that However, direct computations show that $$ \begin{align*} \int_{{\Omega}} \left(\frac{|\mathrm{D} \eta|^2}{2}-\det \mathrm{D} \eta \right) \mathrm{d} |\mu|= \frac{\pi^2}{4L^2}\int_{-L}^L 2\sin^2(0) \sin^2\frac{\pi y}{2L} \mathrm{d} y =0. \end{align*} $$
and
$$ \begin{align*} \int_{{\Omega}} \left(\frac{|\mathrm{D} \eta|^2}{2}-\det \mathrm{D} \eta \right) \mathrm{d} |\mu|= \frac{\pi^2}{4L^2}\int_{-L}^L 2\sin^2(0) \sin^2\frac{\pi y}{2L} \mathrm{d} y =0. \end{align*} $$
and $$ \begin{align*} \int_{{\Omega}} |h'|^2|\nabla \eta_2|^2&= \frac{\pi^2}{4L^2}\int_{(-L,L)^2} |h'|^2(\cos^2\frac{\pi x}{2L}\cos^2 \frac{\pi y}{2L}+\sin^2\frac{\pi x}{2L}\sin^2 \frac{\pi y}{2L}) \\ &= \frac{\pi^2}{4L^2}\times L \times \int_{-L}^L e^{-2|x|} =\frac{\pi^2 (1-e^{-2L})}{4L}, \end{align*} $$
We also observe that
$$ \begin{align*} \int_{{\Omega}} |h'|^2|\nabla \eta_2|^2&= \frac{\pi^2}{4L^2}\int_{(-L,L)^2} |h'|^2(\cos^2\frac{\pi x}{2L}\cos^2 \frac{\pi y}{2L}+\sin^2\frac{\pi x}{2L}\sin^2 \frac{\pi y}{2L}) \\ &= \frac{\pi^2}{4L^2}\times L \times \int_{-L}^L e^{-2|x|} =\frac{\pi^2 (1-e^{-2L})}{4L}, \end{align*} $$
We also observe that $$ \begin{align*} \int_{{\Omega}} (|h'|^2+h^2)\det \mathrm{D} \eta= &\frac{\pi^2}{4L}\int_{-L}^L 2e^{-2|x|} \left( \cos^2\frac{\pi x}{2L}-\sin^2\frac{\pi x}{2 L}\right) =\frac{\pi^2}{2L} \int_{-L}^L e^{-2|x|}\cos \frac{\pi x}{L}\\ &=\frac{\pi^2}{L} \int_{0}^L e^{-2x}\cos \frac{\pi x}{L}=\frac{\pi^2}{L}\text{Re} \int_0^L e^{-2x+\frac{i \pi x}{L}} \\ &=\frac{2\pi^2 L^2 (1+e^{-2L})}{(4L^2+\pi^2)L} =\frac{2\pi^2 L (1+e^{-2L})}{(4L^2+\pi^2)}. \end{align*} $$
$$ \begin{align*} \int_{{\Omega}} (|h'|^2+h^2)\det \mathrm{D} \eta= &\frac{\pi^2}{4L}\int_{-L}^L 2e^{-2|x|} \left( \cos^2\frac{\pi x}{2L}-\sin^2\frac{\pi x}{2 L}\right) =\frac{\pi^2}{2L} \int_{-L}^L e^{-2|x|}\cos \frac{\pi x}{L}\\ &=\frac{\pi^2}{L} \int_{0}^L e^{-2x}\cos \frac{\pi x}{L}=\frac{\pi^2}{L}\text{Re} \int_0^L e^{-2x+\frac{i \pi x}{L}} \\ &=\frac{2\pi^2 L^2 (1+e^{-2L})}{(4L^2+\pi^2)L} =\frac{2\pi^2 L (1+e^{-2L})}{(4L^2+\pi^2)}. \end{align*} $$
 $\mathrm {div} \eta =0$
. Hence, It is easily seen that when L is large enough, this quantity is negative.
$\mathrm {div} \eta =0$
. Hence, It is easily seen that when L is large enough, this quantity is negative. $$ \begin{align*} Q_h(\eta)&= \frac{\pi^2 (1-e^{-2L})}{4L}-\frac{2\pi^2L (1+e^{-2L})}{(4L^2+\pi^2)} \\ &= \frac{\pi^2}{4L(4L^2+\pi^2)}\left[ (4L^2+\pi^2)(1-e^{-2L})-8L^2 (1+e^{-2L}) \right] \\ &= \frac{\pi^2}{4L(4L^2+\pi^2)} \left[ -4L^2+\pi^2-e^{-2L}(12L^2+\pi^2)\right]. \end{align*} $$
$$ \begin{align*} Q_h(\eta)&= \frac{\pi^2 (1-e^{-2L})}{4L}-\frac{2\pi^2L (1+e^{-2L})}{(4L^2+\pi^2)} \\ &= \frac{\pi^2}{4L(4L^2+\pi^2)}\left[ (4L^2+\pi^2)(1-e^{-2L})-8L^2 (1+e^{-2L}) \right] \\ &= \frac{\pi^2}{4L(4L^2+\pi^2)} \left[ -4L^2+\pi^2-e^{-2L}(12L^2+\pi^2)\right]. \end{align*} $$
4.2 The case without magnetic field
In the case without magnetic field, the limiting stability condition never implies any further regularity on the limiting vorticity measure
![]() $\mu $
.
$\mu $
.
Proposition 4.2 Let
![]() $\mu $
be in
$\mu $
be in
![]() $H^{-1}({{\Omega }})$
and U be in
$H^{-1}({{\Omega }})$
and U be in
![]() $H^1({{\Omega }})$
satisfying (1.25), then
$H^1({{\Omega }})$
satisfying (1.25), then
![]() $\tilde {Q}_U(\eta )\geq 0$
for every
$\tilde {Q}_U(\eta )\geq 0$
for every
![]() $\eta $
in
$\eta $
in
![]() ${\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
; with
${\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
; with
![]() $\tilde {Q}_U$
defined in (1.26).
$\tilde {Q}_U$
defined in (1.26).
Proof By using (4.1), we find that for every
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {R}^2)$
,
 $$ \begin{align*} \tilde{Q}_U(\eta)&\geq \int_{{\Omega}} |\mathrm{D} \eta^T\nabla^{\perp} U|^2-|\nabla U|^2 \det \mathrm{D} \eta \\ & =\int_{{\Omega}} \nabla^{\perp} U \otimes \nabla^{\perp} U: \mathrm{D} \eta \mathrm{D} \eta^T -|\nabla U|^2 \det \mathrm{D} \eta \\ &=\int_{{\Omega}} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2}{2}\mathrm{Id}\right): \mathrm{D} \eta \mathrm{D} \eta^T +\int_{{\Omega}} |\nabla U|^2 \left(\frac{|\mathrm{D} \eta|^2}{2}- \det \mathrm{D} \eta \right) \\ &=\int_{{\Omega}} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2}{2}\mathrm{Id}\right) :\left(\mathrm{D} \eta \mathrm{D} \eta^T-\frac{|\mathrm{D} \eta|^2 }{2}\mathrm{Id}\right) \\ & \quad \quad +\int_{{\Omega}} |\nabla U|^2 \left(\frac{|\mathrm{D} \eta|^2 }{2}- \det \mathrm{D} \eta \right). \end{align*} $$
$$ \begin{align*} \tilde{Q}_U(\eta)&\geq \int_{{\Omega}} |\mathrm{D} \eta^T\nabla^{\perp} U|^2-|\nabla U|^2 \det \mathrm{D} \eta \\ & =\int_{{\Omega}} \nabla^{\perp} U \otimes \nabla^{\perp} U: \mathrm{D} \eta \mathrm{D} \eta^T -|\nabla U|^2 \det \mathrm{D} \eta \\ &=\int_{{\Omega}} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2}{2}\mathrm{Id}\right): \mathrm{D} \eta \mathrm{D} \eta^T +\int_{{\Omega}} |\nabla U|^2 \left(\frac{|\mathrm{D} \eta|^2}{2}- \det \mathrm{D} \eta \right) \\ &=\int_{{\Omega}} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2}{2}\mathrm{Id}\right) :\left(\mathrm{D} \eta \mathrm{D} \eta^T-\frac{|\mathrm{D} \eta|^2 }{2}\mathrm{Id}\right) \\ & \quad \quad +\int_{{\Omega}} |\nabla U|^2 \left(\frac{|\mathrm{D} \eta|^2 }{2}- \det \mathrm{D} \eta \right). \end{align*} $$
In the last equality, we have used that
![]() $ \left (\nabla ^{\perp } U \otimes \nabla ^{\perp } U-\frac {|\nabla U|^2}{2}\mathrm {Id}\right ):\mathrm {Id}=\mathrm {tr} (\nabla ^{\perp } U \otimes \nabla ^{\perp } U-\frac {|\nabla U|^2}{2}\mathrm {Id})=0$
. Now we remark that
$ \left (\nabla ^{\perp } U \otimes \nabla ^{\perp } U-\frac {|\nabla U|^2}{2}\mathrm {Id}\right ):\mathrm {Id}=\mathrm {tr} (\nabla ^{\perp } U \otimes \nabla ^{\perp } U-\frac {|\nabla U|^2}{2}\mathrm {Id})=0$
. Now we remark that
![]() $(\nabla ^{\perp } U \otimes \nabla ^{\perp } U-\frac {|\nabla U|^2}{2}\mathrm {Id})=-\left ( \nabla U\otimes \nabla U-\frac {|\nabla U|^2}{2}\mathrm {Id}\right )$
.
$(\nabla ^{\perp } U \otimes \nabla ^{\perp } U-\frac {|\nabla U|^2}{2}\mathrm {Id})=-\left ( \nabla U\otimes \nabla U-\frac {|\nabla U|^2}{2}\mathrm {Id}\right )$
.
We take advantage of the complex structure of
![]() $\mathbb {R}^2\simeq \mathbb {C}$
and, by denoting
$\mathbb {R}^2\simeq \mathbb {C}$
and, by denoting
![]() $\partial _z=(\partial _1-i\partial _2)/2$
and
$\partial _z=(\partial _1-i\partial _2)/2$
and
![]() $\partial _{\bar {z}}=(\partial _1+i\partial _2)/2$
, we can prove that
$\partial _{\bar {z}}=(\partial _1+i\partial _2)/2$
, we can prove that
 $$ \begin{align} \int_{{\Omega}} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2 }{2}\mathrm{Id}\right) :\left(\mathrm{D} \eta \mathrm{D} \eta^T-\frac{|\mathrm{D} \eta|^2 }{2}\mathrm{Id}\right) =8\text{Re} \int_{{\Omega}} \partial_zU \overline {(\partial_{\bar{z}}U)} \partial_z \eta \partial_{\bar{z}} \eta \end{align} $$
$$ \begin{align} \int_{{\Omega}} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2 }{2}\mathrm{Id}\right) :\left(\mathrm{D} \eta \mathrm{D} \eta^T-\frac{|\mathrm{D} \eta|^2 }{2}\mathrm{Id}\right) =8\text{Re} \int_{{\Omega}} \partial_zU \overline {(\partial_{\bar{z}}U)} \partial_z \eta \partial_{\bar{z}} \eta \end{align} $$
 $$ \begin{align} \int_{{\Omega}} |\nabla U|^2\left(\frac{|\mathrm{D} \eta|^2 }{2}- \det \mathrm{D} \eta \right)=4 \int_{{\Omega}} (|\partial_z U|^2+|\partial_{\bar{z}}U|^2)|\partial_{\bar{z}}\eta|^2. \end{align} $$
$$ \begin{align} \int_{{\Omega}} |\nabla U|^2\left(\frac{|\mathrm{D} \eta|^2 }{2}- \det \mathrm{D} \eta \right)=4 \int_{{\Omega}} (|\partial_z U|^2+|\partial_{\bar{z}}U|^2)|\partial_{\bar{z}}\eta|^2. \end{align} $$
Indeed, on the one hand,
 $$ \begin{align*} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2 }{2}\mathrm{Id}\right) :\left(\mathrm{D} \eta \mathrm{D} \eta^T-\frac{|\mathrm{D} \eta|^2 }{2}\mathrm{Id}\right) \\ = \begin{pmatrix} \frac{|\partial_2U|^2-|\partial_1U|^2}{2} & -\partial_2U\partial_1U \\ -\partial_2U\partial_1U & \frac{|\partial_1U|^2-|\partial_2U|^2}{2} \end{pmatrix}: \begin{pmatrix} \frac{|\nabla \eta_1|^2-|\nabla \eta_2|^2}{2} & \nabla \eta_1\cdot \nabla \eta_2 \\ \nabla \eta_1\cdot \nabla \eta_2 & \frac{|\nabla \eta_2|^2-|\nabla \eta_1|^2}{2} \end{pmatrix}\\ = \frac12 (|\partial_2U|^2-|\partial_1U|^2)(|\nabla \eta_1|^2-|\nabla \eta_2|^2)-2 \partial_1U \partial_2U \nabla \eta_1\cdot \nabla \eta_2, \end{align*} $$
$$ \begin{align*} \left(\nabla^{\perp} U \otimes \nabla^{\perp} U-\frac{|\nabla U|^2 }{2}\mathrm{Id}\right) :\left(\mathrm{D} \eta \mathrm{D} \eta^T-\frac{|\mathrm{D} \eta|^2 }{2}\mathrm{Id}\right) \\ = \begin{pmatrix} \frac{|\partial_2U|^2-|\partial_1U|^2}{2} & -\partial_2U\partial_1U \\ -\partial_2U\partial_1U & \frac{|\partial_1U|^2-|\partial_2U|^2}{2} \end{pmatrix}: \begin{pmatrix} \frac{|\nabla \eta_1|^2-|\nabla \eta_2|^2}{2} & \nabla \eta_1\cdot \nabla \eta_2 \\ \nabla \eta_1\cdot \nabla \eta_2 & \frac{|\nabla \eta_2|^2-|\nabla \eta_1|^2}{2} \end{pmatrix}\\ = \frac12 (|\partial_2U|^2-|\partial_1U|^2)(|\nabla \eta_1|^2-|\nabla \eta_2|^2)-2 \partial_1U \partial_2U \nabla \eta_1\cdot \nabla \eta_2, \end{align*} $$
and on the other hand,
 $$ \begin{align*} &16\text{Re} \left( \partial_zU \overline{(\partial_{\bar{z}} U)} \partial_z\eta\partial_{\bar{z}}\eta \right) \\ &=\text{Re} \Big\{ (\partial_1U-i\partial_2U) (\partial_1U-i\partial_2U) \left(\partial_1(\eta_1+i\eta_2)-i\partial_2(\eta_1+i\eta_2)\right) \left(\partial_1(\eta_1+i\eta_2)+i\partial_2(\eta_1+i\eta_2)\right)\Big\}\\ &=\text{Re} \Big\{ (|\partial_1U|^2-|\partial_2U|^2-2i\partial_1U\partial_2U) \Big[ (\partial_1\eta_1+\partial_2\eta_2)(\partial_1\eta_1-\partial_2\eta_2) -(\partial_1\eta_2-\partial_2\eta_1)(\partial_1\eta_2+\partial_2\eta_1) \\ & \quad \quad +i\Big( (\partial_1\eta_2-\partial_2\eta_1)(\partial_1\eta_1-\partial_2\eta_2)+(\partial_1\eta_1+\partial_2\eta_2)(\partial_1\eta_2+\partial_2\eta_1) \Big) \Big] \Big\} \\ &=\text{Re} \Big\{ \left(|\partial_1U|^2-|\partial_2U|^2-2i\partial_1U\partial_2U \right) \left( |\nabla \eta_1|^2-|\nabla \eta_2|^2+2i \nabla \eta_1\cdot \nabla \eta_2 \right) \Big\} \\ &=-\left[(|\partial_2U|^2-|\partial_1U|^2)(|\nabla \eta_1|^2-|\nabla \eta_2|^2)-4 \partial_1U \partial_2U \nabla \eta_1\cdot \nabla \eta_2\right]. \end{align*} $$
$$ \begin{align*} &16\text{Re} \left( \partial_zU \overline{(\partial_{\bar{z}} U)} \partial_z\eta\partial_{\bar{z}}\eta \right) \\ &=\text{Re} \Big\{ (\partial_1U-i\partial_2U) (\partial_1U-i\partial_2U) \left(\partial_1(\eta_1+i\eta_2)-i\partial_2(\eta_1+i\eta_2)\right) \left(\partial_1(\eta_1+i\eta_2)+i\partial_2(\eta_1+i\eta_2)\right)\Big\}\\ &=\text{Re} \Big\{ (|\partial_1U|^2-|\partial_2U|^2-2i\partial_1U\partial_2U) \Big[ (\partial_1\eta_1+\partial_2\eta_2)(\partial_1\eta_1-\partial_2\eta_2) -(\partial_1\eta_2-\partial_2\eta_1)(\partial_1\eta_2+\partial_2\eta_1) \\ & \quad \quad +i\Big( (\partial_1\eta_2-\partial_2\eta_1)(\partial_1\eta_1-\partial_2\eta_2)+(\partial_1\eta_1+\partial_2\eta_2)(\partial_1\eta_2+\partial_2\eta_1) \Big) \Big] \Big\} \\ &=\text{Re} \Big\{ \left(|\partial_1U|^2-|\partial_2U|^2-2i\partial_1U\partial_2U \right) \left( |\nabla \eta_1|^2-|\nabla \eta_2|^2+2i \nabla \eta_1\cdot \nabla \eta_2 \right) \Big\} \\ &=-\left[(|\partial_2U|^2-|\partial_1U|^2)(|\nabla \eta_1|^2-|\nabla \eta_2|^2)-4 \partial_1U \partial_2U \nabla \eta_1\cdot \nabla \eta_2\right]. \end{align*} $$
This proves (4.3), and (4.4) is proved in a similar way.
We are thus led to prove that
Since U is real-valued, it satisfies that
![]() $(\partial _zU)^2=(\partial _zU)\overline {(\partial _{\bar {z}}U)}$
, and from equation (1.25) (see also [Reference Sandier and Serfaty31, Theorem 3] or [Reference Sandier and Serfaty32, Theorem 13.2]), we know that
$(\partial _zU)^2=(\partial _zU)\overline {(\partial _{\bar {z}}U)}$
, and from equation (1.25) (see also [Reference Sandier and Serfaty31, Theorem 3] or [Reference Sandier and Serfaty32, Theorem 13.2]), we know that
![]() $(\partial _zU)^2$
is holomorphic in
$(\partial _zU)^2$
is holomorphic in
![]() ${{\Omega }}$
. We can invoke Theorem 1.10 in [Reference Iwaniec and Onninen18] to conclude that (4.5) is true. Note that in the statement of Theorem 1.10 in [Reference Iwaniec and Onninen18], the quantity appearing is
${{\Omega }}$
. We can invoke Theorem 1.10 in [Reference Iwaniec and Onninen18] to conclude that (4.5) is true. Note that in the statement of Theorem 1.10 in [Reference Iwaniec and Onninen18], the quantity appearing is
But the proof of the nonnegativity of this quantity for U such that
![]() $ (\partial _zU)\overline {(\partial _{\bar {z}}U)}$
is holomorphic and for all
$ (\partial _zU)\overline {(\partial _{\bar {z}}U)}$
is holomorphic and for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {C})$
adapts with the minus sign (i.e., for the quantity appearing in (4.5)). Indeed, the proof of this fact rests upon the inequality
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {C})$
adapts with the minus sign (i.e., for the quantity appearing in (4.5)). Indeed, the proof of this fact rests upon the inequality
valid for U satisfying that
![]() $ (\partial _zU)\overline {(\partial _{\bar {z}}U)}$
is holomorphic and for all
$ (\partial _zU)\overline {(\partial _{\bar {z}}U)}$
is holomorphic and for all
![]() $\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {C})$
, cf. Lemma 1.11 in [Reference Iwaniec and Onninen18], and then we use
$\eta \in {\mathcal C}^{\infty }_c({{\Omega }},\mathbb {C})$
, cf. Lemma 1.11 in [Reference Iwaniec and Onninen18], and then we use
instead of
in the proof of Theorem 1.10 in [Reference Iwaniec and Onninen18] to arrive at (4.5).
5 Conclusion and perspectives
We have shown, in a certain regime of applied magnetic field (1.9) and for solutions satisfying the energy bound (1.8), how to pass to the limit in the second inner variations of the energy
![]() $\mathrm {GL}_{\varepsilon }$
if we assume the convergence of energies (H). Since the
$\mathrm {GL}_{\varepsilon }$
if we assume the convergence of energies (H). Since the
![]() $\Gamma $
- limit
$\Gamma $
- limit
![]() $E^\lambda $
of the sequence of energies
$E^\lambda $
of the sequence of energies
![]() $\mathrm {GL}_{\varepsilon }$
is convex, whereas the energies
$\mathrm {GL}_{\varepsilon }$
is convex, whereas the energies
![]() $\mathrm {GL}_{\varepsilon }$
are not convex, it is not direct to guess a limiting criticality condition (respectively a limiting stability condition) for solutions to (1.4), (respectively stable solutions) to (1.1). In particular, whereas limiting vorticity measures of solutions to (1.4) satisfy
$\mathrm {GL}_{\varepsilon }$
are not convex, it is not direct to guess a limiting criticality condition (respectively a limiting stability condition) for solutions to (1.4), (respectively stable solutions) to (1.1). In particular, whereas limiting vorticity measures of solutions to (1.4) satisfy
![]() $-\Delta h+h=\mu $
in
$-\Delta h+h=\mu $
in
![]() ${{\Omega }}$
with h which is stationary (i.e., critical for the inner variations) for
${{\Omega }}$
with h which is stationary (i.e., critical for the inner variations) for
![]() $\mathcal {L}(h)=\int _{{\Omega }} (|\nabla h|^2+h^2)$
, it is not true that stable limiting vorticities of stable solutions verify that the second inner variation of
$\mathcal {L}(h)=\int _{{\Omega }} (|\nabla h|^2+h^2)$
, it is not true that stable limiting vorticities of stable solutions verify that the second inner variation of
![]() $\mathcal {L}$
is nonnegative since this second inner variation can be computed to be equal to
$\mathcal {L}$
is nonnegative since this second inner variation can be computed to be equal to
The right limiting stable condition is given by (1.17)–(1.16). The example analyzed in Section 4 tends to show that the stability condition does not prevent limiting vorticity measures to concentrate on curves and that no further regularity for stable limiting vorticity could be deduced. This is definitely the case for the GL equations without magnetic field as shown by Proposition 4.2.
As for [Reference Sandier and Serfaty31, Theorem 1], our result Theorem 1.3 is interesting only if the total number of vortices
![]() $N_{\varepsilon }=\sum _{i=1}^{M_{\varepsilon }} |d_i^{\varepsilon }|$
appearing in (1.11) is of the same order as
$N_{\varepsilon }=\sum _{i=1}^{M_{\varepsilon }} |d_i^{\varepsilon }|$
appearing in (1.11) is of the same order as
![]() $h_{\operatorname {\mathrm {\text {ex}}}}$
. As explained in [Reference Sandier and Serfaty31, Theorem 2], for
$h_{\operatorname {\mathrm {\text {ex}}}}$
. As explained in [Reference Sandier and Serfaty31, Theorem 2], for
![]() $\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
a family of solutions to (1.4), if
$\{(u_{\varepsilon },A_{\varepsilon })\}_{{\varepsilon }>0}$
a family of solutions to (1.4), if
![]() $ N_{\varepsilon } \gg h_{\operatorname {\mathrm {\text {ex}}}}$
, then
$ N_{\varepsilon } \gg h_{\operatorname {\mathrm {\text {ex}}}}$
, then
![]() $\mu (u_{\varepsilon },A_{\varepsilon })/N_{\varepsilon }$
converges to zero in the sense of measures, whereas if
$\mu (u_{\varepsilon },A_{\varepsilon })/N_{\varepsilon }$
converges to zero in the sense of measures, whereas if
![]() $ N_{\varepsilon }\ll h_{\operatorname {\mathrm {\text {ex}}}}$
, then
$ N_{\varepsilon }\ll h_{\operatorname {\mathrm {\text {ex}}}}$
, then
![]() $\mu (u_{\varepsilon },A_{\varepsilon })/N_{\varepsilon }\rightharpoonup \mu $
with
$\mu (u_{\varepsilon },A_{\varepsilon })/N_{\varepsilon }\rightharpoonup \mu $
with
![]() $\mu \nabla h_0=0$
and
$\mu \nabla h_0=0$
and
![]() $h_0$
the solution to
$h_0$
the solution to
![]() $-\Delta h_0+h_0=0$
in
$-\Delta h_0+h_0=0$
in
![]() ${{\Omega }}$
with
${{\Omega }}$
with
![]() $h=1$
on
$h=1$
on
![]() $\partial {{\Omega }}$
, and hence, the support of
$\partial {{\Omega }}$
, and hence, the support of
![]() $\mu $
is included in the set of critical points of
$\mu $
is included in the set of critical points of
![]() $h_0$
. For minimizers, it was proved in [Reference Sandier and Serfaty30, Reference Sandier and Serfaty32] that vortices accumulate near minimizing points of
$h_0$
. For minimizers, it was proved in [Reference Sandier and Serfaty30, Reference Sandier and Serfaty32] that vortices accumulate near minimizing points of
![]() $h_0$
. We can also ask if there exist supplementary conditions in the limit
$h_0$
. We can also ask if there exist supplementary conditions in the limit
![]() ${\varepsilon }\to 0$
for stable solutions with
${\varepsilon }\to 0$
for stable solutions with
![]() $ N_{\varepsilon }\ll h_{\operatorname {\mathrm {\text {ex}}}}$
such as vortices accumulating toward stable critical points of
$ N_{\varepsilon }\ll h_{\operatorname {\mathrm {\text {ex}}}}$
such as vortices accumulating toward stable critical points of
![]() $h_0$
in
$h_0$
in
![]() ${{\Omega }}$
. However, this seems to require different techniques than the ones used in this paper.
${{\Omega }}$
. However, this seems to require different techniques than the ones used in this paper.
Appendix
Here, we recall two results used in the proof of main theorems. These results aim at describing the limiting vorticities near regular points of the limiting field h. Note that we can define regular and critical points of h since it is proved in [Reference Sandier and Serfaty32, Theorem 13.1] that
![]() $|\nabla h|^2$
is continuous in
$|\nabla h|^2$
is continuous in
![]() ${{\Omega }}$
.
${{\Omega }}$
.
Theorem 5.1 [Reference Rodiac27, Theorem 3.1]
Let
![]() $h\in H^1({{\Omega }})$
and
$h\in H^1({{\Omega }})$
and
![]() $\mu \in \mathcal {M}({{\Omega }})$
be such that
$\mu \in \mathcal {M}({{\Omega }})$
be such that
![]() $-\Delta h+h=\mu $
and
$-\Delta h+h=\mu $
and
![]() $\sum _{j=1}^2 \partial _j\left [ 2\partial _i h\partial _j h-\left ( |\nabla h|^2+h^2\right ) \delta _{ij}\right ]=0$
in
$\sum _{j=1}^2 \partial _j\left [ 2\partial _i h\partial _j h-\left ( |\nabla h|^2+h^2\right ) \delta _{ij}\right ]=0$
in
![]() ${{\Omega }}$
for
${{\Omega }}$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $x_0\in \mathrm {supp\,} \mu $
be such that
$x_0\in \mathrm {supp\,} \mu $
be such that
![]() $|\nabla h(x_0)|\neq 0$
. Then there exists
$|\nabla h(x_0)|\neq 0$
. Then there exists
![]() $R>0$
and
$R>0$
and
![]() $H\in {\mathcal C}^{1,\alpha }(B(x_0,R))$
for every
$H\in {\mathcal C}^{1,\alpha }(B(x_0,R))$
for every
![]() $0<\alpha <1$
such that
$0<\alpha <1$
such that
and
![]() $\nabla H(x)\neq 0$
for every
$\nabla H(x)\neq 0$
for every
![]() $x\in B(x_0,R)$
. Furthermore,
$x\in B(x_0,R)$
. Furthermore,
![]() $\mu _{\lfloor B(x_0,R)}=+2|\nabla h|\mathcal {H}^1_{\lfloor \Gamma }$
or
$\mu _{\lfloor B(x_0,R)}=+2|\nabla h|\mathcal {H}^1_{\lfloor \Gamma }$
or
![]() $\mu _{\lfloor B(x_0,R)}=-2|\nabla h|\mathcal {H}^1_{\lfloor \Gamma }$
.
$\mu _{\lfloor B(x_0,R)}=-2|\nabla h|\mathcal {H}^1_{\lfloor \Gamma }$
.
Theorem 5.2 [Reference Rodiac26, Theorem 1.3]
Let
![]() $h\in H^1({{\Omega }})$
and
$h\in H^1({{\Omega }})$
and
![]() $\mu \in \mathcal {M}({{\Omega }})$
be such that
$\mu \in \mathcal {M}({{\Omega }})$
be such that
![]() $\Delta h=\mu $
and
$\Delta h=\mu $
and
![]() $\sum _{j=1}^2 \partial _j\left [ 2\partial _i h\partial _j h- |\nabla h|^2 \delta _{ij}\right ]=0$
in
$\sum _{j=1}^2 \partial _j\left [ 2\partial _i h\partial _j h- |\nabla h|^2 \delta _{ij}\right ]=0$
in
![]() ${{\Omega }}$
for
${{\Omega }}$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $x_0\in \mathrm {supp\,} \mu $
be such that
$x_0\in \mathrm {supp\,} \mu $
be such that
![]() $|\nabla h(x_0)|\neq 0$
. Then there exists
$|\nabla h(x_0)|\neq 0$
. Then there exists
![]() $R>0$
and H a harmonic function in
$R>0$
and H a harmonic function in
![]() $B(x_0,R)$
such that
$B(x_0,R)$
such that
and
![]() $\nabla H(x)\neq 0$
for every
$\nabla H(x)\neq 0$
for every
![]() $x\in B(x_0,R)$
. Furthermore,
$x\in B(x_0,R)$
. Furthermore,
![]() $\mu _{\lfloor B(x_0,R)}=+2|\nabla h|\mathcal {H}^1_{\lfloor \tilde {\Gamma }}$
or
$\mu _{\lfloor B(x_0,R)}=+2|\nabla h|\mathcal {H}^1_{\lfloor \tilde {\Gamma }}$
or
![]() $\mu _{\lfloor B(x_0,R)}=-2|\nabla h|\mathcal {H}^1_{\lfloor \tilde {\Gamma }}$
.
$\mu _{\lfloor B(x_0,R)}=-2|\nabla h|\mathcal {H}^1_{\lfloor \tilde {\Gamma }}$
.