Article contents
Sommes friables d'exponentielles et applications
Published online by Cambridge University Press: 20 November 2018
Abstract
An integer is said to be 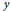 $y$-friable if its greatest prime factor is less than
$y$-friable if its greatest prime factor is less than 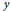 $y$. In this paper, we obtain estimates for exponential sums over
$y$. In this paper, we obtain estimates for exponential sums over 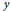 $y$-friable numbers up to
$y$-friable numbers up to 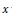 $x$ which are non-trivial when
$x$ which are non-trivial when 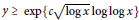 $y\,\ge \,\exp \left\{ c \right.\sqrt{\log \,x\,}\log \,\log \,\left. x \right\}$. As a consequence, we obtain an asymptotic formula for the number of
$y\,\ge \,\exp \left\{ c \right.\sqrt{\log \,x\,}\log \,\log \,\left. x \right\}$. As a consequence, we obtain an asymptotic formula for the number of 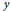 $y$-friable solutions to the equation
$y$-friable solutions to the equation 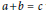 $a\,+\,b\,=\,c$ which is valid unconditionally under the same assumption. We use a contour integration argument based on the saddle point method, as developped in the context of friable numbers by Hildebrand and Tenenbaum, and used by Lagarias, Soundararajan and Harper to study exponential and character sums over friable numbers.
$a\,+\,b\,=\,c$ which is valid unconditionally under the same assumption. We use a contour integration argument based on the saddle point method, as developped in the context of friable numbers by Hildebrand and Tenenbaum, and used by Lagarias, Soundararajan and Harper to study exponential and character sums over friable numbers.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 1
- Cited by


