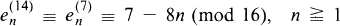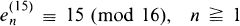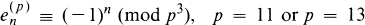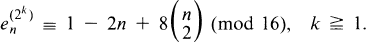Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gessel, Ira M
1990.
Symmetric functions and P-recursiveness.
Journal of Combinatorial Theory, Series A,
Vol. 53,
Issue. 2,
p.
257.
Smith, John Howard
1993.
Combinatorial congruences fromp-subgroups of the symmetric group.
Graphs and Combinatorics,
Vol. 9,
Issue. 2-4,
p.
293.
Guo, Victor J.W.
and
Zeng, Jiang
2006.
Some arithmetic properties of the q-Euler numbers and q-Salié numbers.
European Journal of Combinatorics,
Vol. 27,
Issue. 6,
p.
884.
Mendes, Anthony
Remmel, Jeffrey B.
and
Riehl, Amanda
2010.
Permutation Patterns.
p.
259.
Fuller, Evan
and
Remmel, Jeffrey
2011.
Quasi-symmetric functions and up–down compositions.
Discrete Mathematics,
Vol. 311,
Issue. 16,
p.
1754.
Reineke, Markus
2011.
Cohomology of quiver moduli, functional equations, and integrality of Donaldson–Thomas type invariants.
Compositio Mathematica,
Vol. 147,
Issue. 3,
p.
943.
Straub, Armin
2014.
Multivariate Apéry numbers and supercongruences of rational functions.
Algebra & Number Theory,
Vol. 8,
Issue. 8,
p.
1985.
Osburn, Robert
Sahu, Brundaban
and
Straub, Armin
2016.
Supercongruences for sporadic sequences.
Proceedings of the Edinburgh Mathematical Society,
Vol. 59,
Issue. 2,
p.
503.
Zhang, Yong
and
Yuan, Peisen
2021.
Proof of a Dwork-type supercongruence by induction.
AIMS Mathematics,
Vol. 6,
Issue. 10,
p.
11568.
Zhang, Yong
2022.
Some conjectural supercongruences related to Bernoulli and Euler numbers.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 3,
Mao, Guo-Shuai
Li, Danrui
and
Ma, Xinmin
2023.
On some congruences involving Apéry-like numbers Sn.
Journal of Difference Equations and Applications,
Vol. 29,
Issue. 2,
p.
181.
Straub, Armin
2024.
Gessel–Lucas congruences for sporadic sequences.
Monatshefte für Mathematik,
Vol. 203,
Issue. 4,
p.
883.
Alinquant, Brendan
and
Osburn, Robert
2024.
On sporadic sequences.
Monatshefte für Mathematik,
Vol. 205,
Issue. 2,
p.
217.
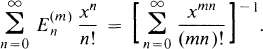
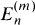 is zero unless m divides n, we shall write
is zero unless m divides n, we shall write 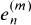 for
for 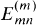 . Leeming and MacLeod [12] recently gave some congruences for these numbers. They found congruences (mod 16) for
. Leeming and MacLeod [12] recently gave some congruences for these numbers. They found congruences (mod 16) for 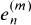 where m = 3, 6, 8, 12, and 16. Thus for m = 3, their congruence is
where m = 3, 6, 8, 12, and 16. Thus for m = 3, their congruence is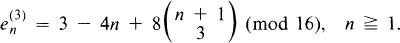
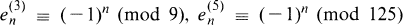 , and
, and 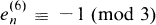 , and they made several conjectures which may be stated as follows:
, and they made several conjectures which may be stated as follows: