Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T16:28:21.113Z Has data issue: false hasContentIssue false
  • English
  • Français

The Seven Dimensional Perfect DelaunayPolytopes and Delaunay Simplices

Published online by Cambridge University Press:  20 November 2018

Mathieu Dutour Sikirić
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a lattice $L$ of 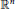${{\mathbb{R}}^{n}}$, a sphere 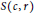$S\left( c,r \right)$ of center $c$ and radius $r$ is called empty if for any 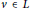$v\,\in \,L$ we have 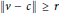$\parallel v\,-\,c\parallel \,\,\ge \,r$. Then the set 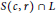$S\left( c,r \right)\,\cap \,L$ is the vertex set of a 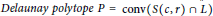$Delaunay\,polytope\,P\,=\,\text{conv}\left( S\left( c,r \right)\cap L \right)$. A Delaunay polytope is called perfect if any affine transformation 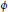$\phi $ such that 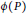$\phi \left( P \right)$ is a Delaunay polytope is necessarily an isometry of the space composed with an homothety.

Perfect Delaunay polytopes are remarkable structures that exist only if 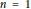$n\,=\,1$ or 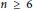$n\,\ge \,6$, and they have shown up recently in covering maxima studies. Here we give a general algorithm for their enumeration that relies on the Erdahl cone. We apply this algorithm in dimension seven, which allows us to find that there are only two perfect Delaunay polytopes: 321, which is a Delaunay polytope in the root lattice 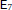${{\text{E}}_{7}}$, and the Erdahl Rybnikov polytope.

We then use this classification in order to get the list of all types of Delaunay simplices in dimension seven and found that there are eleven types.

Keywords

11H0611H31Delaunay polytopeenumerationpolyhedral methods
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 5 , 01 October 2017 , pp. 1143 - 1168
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Avis, D., The 1rs program. 2015 http://cgm.cs. mcgill.ca/~avis/C/lrslib/USERGUIDE.html Google Scholar
[2] Baranovskiĭ, E. P., The conditions for a simplex of 6-dimensional lattice to be l-simplex. (Russian), Ivan. Univ. 2(1999), no. 3,18–24.Google Scholar
[3] Barvinok, A., A course in convexity. Graduate Studies in Mathematics, 54, American Mathematical Society, Providence, RI, 2002.Google Scholar
[4] Bremner, D., Dutour Sikiric, M., D. Pasechnik, V., Rehn, T., and Schiirmann, A., Computing symmetry groups of polyhedra. LMS J. Comput. Math. 17(2014), no. 1, 565–581,http://dx.doi.Org/10.1112/S14611 57014000400 Google Scholar
[5] Bremner, D., Dutour Sikiric, M., and Schiirmann, A., Polyhedral representation conversion up to symmetries. In: Polyhedral computation, CRM Proc. Lecture Notes, 48, American Mathematical Society, Providence, RI, 2009, pp. 45–71.Google Scholar
[6] Christof, T. and Reinelt, G., Combinatorial optimization and smallpolytopes. Top 4(1996), no. 1, 1–64 http://dx.doi.org/10.1007/BF02568602 Google Scholar
[7] De Loera, J. A., Rambau, J., and Santos, F., Triangulations. Algorithms and Computations in Mathematics, 25, Springer-Verlag, Berlin, 2010.http://dx.doi.org/10.1007/978-3-642-12971-1 Google Scholar
[8] Deza, M. and Dutour, M., The hypermetric cone on seven vertices. Experiment. Math. 12(2003), no. 4,433–440.http://dx.doi.org/10.1080/10586458.2003.10504511 Google Scholar
[9] Deza, M. and Dutour Sikirić, M., Enumeration of the facets of cut polytopes over some highly symmetric graphs. Int. Trans. Oper. Res., to appear. Google Scholar
[10] Deza, M., V. Grishukhin, P., and Laurent, M., The symmetries of the cut polytope and of some relatives. In: Applied geometry and discrete mathematics, DIMACS Ser. Discrete Math. Theoret. Comput. Sci., 4, American Mathematical Society, Providence, RI, 1991, pp. 205–220.Google Scholar
[11] Deza, M., Grishukhin, V. P., and Laurent, M., Extreme hypermetrics and L-polytopes. In: Sets, graphs and numbers (Budapest, 1991), Colloq. Math. Soc. János Bolyai, 60, North-Holland, Amsterdam, 1992, pp. 157–209.Google Scholar
[12] Deza, M. M. and Laurent, M., Geometry of cuts and metrics. Algorithms and Combinatorics, 15, Springer, Heidelberg, 2010.http://dx.doi.org/10.1007/978-3-642-04295-9 Google Scholar
[13] Dutour, M., The six-dimensional Delaunay polytopes. European J. Combin. 25(2004), no. 4, 535–548.http://dx.doi.Org/10.1016/j.ejc.2003.07.004 Google Scholar
[14] Dutour, M., Infinite series of extreme Delaunay polytopes. European J. Combin. 26(2005), no. 1, 129–132.http://dx.doi.Org/10.1016/j.ejc.2 003.11.002 Google Scholar
[15] Dutour, M., Erdahl, R. M., and Rybnikov, K., Perfect Delaunay polytopes in low dimensions. Integers 7(2007), A39, 49.Google Scholar
[16] Dutour, M. and Rybnikov, K., A new algorithm in geometry of numbers. Proceedinga of 4th International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2007), IEEE computer society, 2009, pp. 182–188.Google Scholar
[17] Dutour Sikirić, M., Polyhedral. 2015.http://mathieudutour.altervista.org/Polyhedral/index.html Google Scholar
[18] Dutour Sikirić, M. and Grishukhin, V. P., How to compute the rank of a Delaunay polytope. European J. Combin. 28(2007), no. 3, 762–773.http://dx.doi.Org/10.1016/j.ejc.2005.12.007 Google Scholar
[19] Dutour Sikirić, M. and Rybnikov, K., Perfect but not generating delaunay polytopes. Symmetry Culture and Science, Tesselation II, 22, Symmetrion, 2011, pp. 317–325.Google Scholar
[20] Dutour Sikirić, M., Schiirmann, A., and Vallentin, F., A generalization ofVoronoi-s reduction theory and its application. Duke Math. J. 142(2008), no. 1,127–164.Google Scholar
[21] Dutour Sikirić, M., Schiirmann, A., and Vallentin, F., Complexity and algorithms for computing Voronoi cells of lattices. Math. Comp. 78(2009), no. 267,1713–1731. http://dx.doi.org/10.1090/S002 5-5718-09-02224-8 Google Scholar
[22] Dutour Sikirić, M., Schiirmann, A., and Vallentin, F., Inhomogeneous extreme forms. Ann. Inst. Fourier (Grenoble) 62(2012), no. 6, 2227–2255.http://dx.doi.org/10.5802/aif.2748 Google Scholar
[23] Erdahl, R. M., A cone of inhomogeneous second-order polynomials. Discrete Comput. Geom. 8(1992), no. 4, 387–416.http://dx.doi.org/10.1007/BF02293055 Google Scholar
[24] Erdahl, R. M. and Rybnikov, K., An infinite series of perfect quadratic forms and big Delaunay simplices in . Tr. Mat. Inst. Steklova 239(2002), Diskret. Geom. i Geom. Chisel, 170–178.Google Scholar
[25] Erdahl, R. M., Voronoi-Dickson hypothesis on perfect forms and L-types. In: Rendiconti del Circolo Matematiko di Palermo, Serie II, LII, part I, Symmetrion, 2002, pp. 279–296.Google Scholar
[26] Fukuda, K., The cdd program. 2015.http://www.ifor.math.ethz.ch/n-fukuda/cddnhome/cdd.html Google Scholar
[27] Grishukhin, V. P., Infinite series of extreme Delaunay polytopes. European J. Combin. 27(2006), no. 4, 481–495.http://dx.doi.Org/10.1016/j.ejc.2005.02.002 Google Scholar
[28] The GAP group, GAP—groups, algorithms, and permutations, version 4.4.6. 2015. http://www.gap-system.org Google Scholar
[29] Hans-Gill, R. J., Raka, M., and Sehmi, R., On conjectures of Minkowski and Woods for n = 7. J. Number Theory 129(2009), no. 5,1011–1033. http://dx.doi.Org/10.1016/j.jnt.2008.10.020 Google Scholar
[30] Hans-Gill, R. J., Estimates on conjectures of Minkowski and Woods. Indian J. Pure Appl. Math. 41(2010), no. 4, 595–606.http://dx.doi.org/10.1007/s13226-010-0034-9 Google Scholar
[31] Hans-Gill, R. J., Estimates on conjectures of Minkowski and Woods II. Indian J. Pure Appl. Math. 42(2011), no. 5, 307–333.http://dx.doi.org/10.1007/s13226-011-0021-9 Google Scholar
[32] Hans-Gill, R. J., On conjectures of Minkowski and Woods for n = 8. Acta Arith. 147(2011), no. 4, 337–385.http://dx.doi.Org/10.4064/aa147-4-3 Google Scholar
[33] Keller, W., Martinet, J., and Schürmann, A., On classifying Minkowskian sublattices. Math. Comp. 81(2012), no. 278, 1063–1092.http://dx.doi.org/10.1090/S0025-5718-2011-02528-7 Google Scholar
[34] Koksma, J. F., Diophantische Approximationen. Springer-Verlag, Berlin-New York, 1974.Google Scholar
[35] Martinet, J., Perfect lattices in Euclidean spaces. Grundlehren der Mathematischen Wissenschaften, 327, Springer-Verlag, Berlin, 2003.http://dx.doi.org/10.1007/978-3-662-05167-2 Google Scholar
[36] McKay, B. D. and Piperno, A., nauty and traces, http://cs.anu.edu.au/people/bdm/nauty/ Google Scholar
[37] McMullen,, C. T. Minkowski's conjecture, well-rounded lattices and topological dimension. J. Amer. Math. Soc. 18(2005), no. 3, 711–734.http://dx.doi.Org/10.1090/S0894-0347-05-00483-2 Google Scholar
[38] Ryskov, S. S. and Baranovskiĭ, E. P., Repartitioning complexes in n-dimensional lattices (with full description for n ≥ 6). In: Voronoi impact on modern science, Institute of Mathematics, Kyiv, 1998, pp. 115–124.Google Scholar
[39] Santos, F., Schürmann, A., and Vallentin, F., Lattice Delone simplices with super-exponential volume. European J. Combin. 28(2007), no. 3, 801–806. http://dx.doi.Org/10.1016/j.ejc.2005.12.003 Google Scholar
[40] Schrijver, A., Theory of linear and integer programming. Wiley-Interscience Series in Discrete Mathematics, John Wiley & Sons, Ltd., Chichester, 1986, A Wiley-Interscience Publication. Google Scholar
[41] Schürmann, A., Computational geometry of positive definite quadratic forms. University Lecture Series, 48, American Mathematical Society, Providence, RI, 2009.Google Scholar
[42] Shapiraand, U. Weiss, B., On stable lattices and the diagonal group. arxiv:1309.4025 Google Scholar
[43] M. D.|Sikirić, A. Schiirmann, and F. Vallentin, Classification of eight-dimensional perfect forms. Electron. Res. Announc. Amer. Math. Soc. 13(2007), 21–32.http://dx.doi.Org/10.1090/S1079-6762-07-001 71-0 Google Scholar
[44] Voronoi, G., Nouvelles applications des paramètres continues à la théorie des formes quadratiques 1: Sur quelques propriétés des formes quadratiques positives parfaites. J. Reine Angew. Math 133(1908), no. 1, 97–178.Google Scholar
[45] Voronoi, G., Nouvelles applications des paramètres continus à la théorie des formes quadratiques 2: Recherches sur les parallélloèdres primitifs. J. Reine Angew. Math 134(1908), no. 1,198–287.Google Scholar
[46] Ziegler, G. M., Lectures on polytopes. Graduate Texts in Mathematics, 152, Springer-Verlag, New York, 1995.http://dx.doi.org/10.1007/978-1-4613-8431-1 Google Scholar