Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bochnak, Jacek
and
Kucharz, Wojciech
1979.
Sur les germes d’applications differentiables à singularités isolées.
Transactions of the American Mathematical Society,
Vol. 252,
Issue. 0,
p.
115.
Guimarães, Luiz Carlos
1980.
Functional Differential Equations and Bifurcation.
Vol. 799,
Issue. ,
p.
140.
Bekka, K.
and
Koike, S.
1998.
The Kuo condition, an inequality of Thom's type and (C)-regularity.
Topology,
Vol. 37,
Issue. 1,
p.
45.


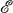 (respectively
(respectively 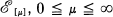 ) denote the ring of germs at 0 ∈
) denote the ring of germs at 0 ∈ 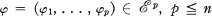 where
where 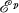 is the space of all germs of
is the space of all germs of 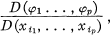
 Let
Let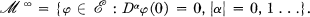
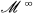 is an ideal in
is an ideal in  where
where 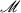 is the (unique) maximal ideal of
is the (unique) maximal ideal of 