Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-02T23:40:55.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of the Fundamental Group of an 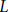$L$–Punctured Sphere Generated by Products of Lagrangian Involutions

Published online by Cambridge University Press:  20 November 2018

Florent Schaffhauser
Florent Schaffhauser*
Affiliation:
Institut de Mathématiques, Université Pierre et Marie Curie-Paris 6, 4, place Jussieu F-75252 Paris Cedex 05 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we characterize unitary representations of 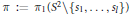$\pi \text{ }:=\text{ }\pi {{\text{ }}_{1}}({{S}^{2}}\backslash \{{{s}_{1}},\ldots ,{{s}_{l}}\})$ whose generators 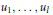${{u}_{1}},\,\ldots ,\,{{u}_{l}}$ (lying in conjugacy classes fixed initially) can be decomposed as products of two Lagrangian involutions 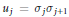${{u}_{j}}\,=\,{{\sigma }_{j}}{{\sigma }_{j+1}}$ with 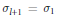${{\sigma }_{l+1}}\,=\,{{\sigma }_{1}}$. Our main result is that such representations are exactly the elements of the fixed-point set of an anti-symplectic involution defined on the moduli space 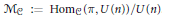${{\mathcal{M}}_{C}}\,:\,=\,\text{Ho}{{\text{m}}_{C}}(\pi ,\,U(n))\,/\,U(n)$. Consequently, as this fixed-point set is non-empty, it is a Lagrangian submanifold of 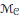${{\mathcal{M}}_{C}}$. To prove this, we use the quasi-Hamiltonian description of the symplectic structure of 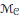${{\mathcal{M}}_{C}}$ and give conditions on an involution defined on a quasi-Hamiltonian 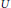$U$-space 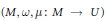$(M,\,\omega ,\,\mu :\,M\to \,U)$ for it to induce an anti-symplectic involution on the reduced space 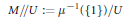$M//U:=\,{{\mu }^{-1}}\,(\{1\})/U$.

Keywords

53D2053D30momentum mapsmoduli spacesLagrangian submanifoldsanti-symplectic involutionsquasi-Hamiltonian
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 4 , 01 August 2007 , pp. 845 - 879
Copyright
Copyright © Canadian Mathematical Society 2007

References

[AW] Agnihotri, S. and Woodward, C., Eigenvalues of products of unitary matrices and quantum Schubert calculus. Math. Res. Lett. 5(1998), no. 6, 817–836.Google Scholar
[AKM] Alekseev, A., Kosmann-Schwarzbach, Y., and Meinrenken, E., Quasi-Poisson manifolds. Canad. J. Math. 54(2002), no. 1, 3–29.Google Scholar
[AM] Alekseev, A. and Malkin, A., Symplectic structure of the moduli space of flat connection[s] on a Riemann surface. Comm. Math. Phys. 169(1995), no. 1, 99–119.Google Scholar
[AMM] Alekseev, A., Malkin, A., and Meinrenken, E., Lie group valued moment maps. J. Differential Geom. 48(1998), no. 3, 445–495.Google Scholar
[AMW] Alekseev, A., Meinrenken, E., and Woodward, C., Linearization of Poisson actions and singular values of matrix products. Ann. Inst. Fourier (Grenoble) 51(2001), no. 6, 1691–1717.Google Scholar
[At] Atiyah, M. F., Convexity and commuting Hamiltonians. Bull. London Math. Soc. 14(1982), no. 1, 1–15.Google Scholar
[AB] Atiyah, M. F. and Bott, R., The Yang-Mills equations over Riemann surfaces. Philos. Trans. Roy. Soc. London Ser. A 308(1983), no. 1505, 523–615.Google Scholar
[Be] Belkale, P., Local systems on ℙ1\S for S a finite set. Compositio Math. 129(2001), no. 1, 67–86.Google Scholar
[Bi1] Biswas, I., A criterion for the existence of a parabolic stable bundle of rank two over the projective line. Internat. J. Math. 9(1998), no. 5, 523–533.Google Scholar
[Bi2] Biswas, I., On the existence of unitary flat connections over the punctured sphere with given local monodromy around the punctures. Asian J. Math. 3(1999), no. 2, 333–344.Google Scholar
[Du] Duistermaat, J. J., Convexity and tightness for restrictions of Hamiltonian functions to fixed point sets of an antisymplectic involution. Trans. Amer. Math. Soc. 275(1983), no. 1, 417–429.Google Scholar
[EL] Evens, S. and Lu, J. H., Thompson's conjecture for real semi-simple Lie groups. In: The Breadth of Symplectic and Poisson Geometry. Prog.Math. 232, Birkhäuser Boston, Boston, MA, 2005, pp. 121–137.Google Scholar
[Fa] Falbel, E., Finite groups generated by involutions on Lagrangian planes in ℂ2 . Canad. Math. Bull. 44(2001), no. 4, 408–419.Google Scholar
[FMS] Falbel, E., Marco, J. P., and Schaffhauser, F., Classifying triples of Lagrangians in a Hermitian vector space. Topology Appl. 144(2004), no. 1-3, 1–27.Google Scholar
[FW] Falbel, E. and R.Wentworth, Eigenvalues of products of unitary matrices and Lagrangian involutions. Topology 45(2006), no. 1, 65–9.Google Scholar
[FH] Foth, P. and Hu, Y., Toric degenerations of weight varieties and applications. In: Travaux mathématiques 16. Université du Luxembourg, Luxembourg, 2005, pp. 87–105.Google Scholar
[Fu] Fulton, W., Eigenvalues of sums of Hermitian matrices (after A. Klyachko). Astérisque no. 252 (Exp. no. 845), 255–269, 1998.Google Scholar
[Ga] Galitzer, A. J., On the moduli space of closed polygonal linkages on the 2-sphere. Ph.D. thesis, University of Maryland, 1997.Google Scholar
[Go] Goldman, W. M., The symplectic nature of fundamental groups of surfaces. Adv. in Math. 54(1984), no. 2, 200–225.Google Scholar
[GHJW] Guruprasad, K., Huebschmann, J., Jeffrey, L., and Weinstein, A., Group systems, groupoids, and moduli spaces of parabolic pundles. Duke Math. J. 89(1997), no. 2, 377–412.Google Scholar
[He] Helgason, S., Differential Geometry, Lie Groups and Symmetric Spaces. Graduate Series in Mathematics 34, American Mathematical Society, Providence, RI, 2001.Google Scholar
[Je] Jeffrey, L., Extended moduli spaces of flat connections on Riemann surfaces. Math. Ann. 298(1994), no. 4, 667–692.Google Scholar
[JW] Jeffrey, L. and Weitsman, J., Bohr-Sommerfeld orbits in the moduli space of flat connections and the Verlinde dimension formula. Comm. Math. Phys. 150(1992), no. 3, 593–630.Google Scholar
[KM] Kapovich, M. and Millson, J., On the moduli space of a spherical polygonal linkage. Canad. Math. Bull. 42(1999), no. 3, 307–320.Google Scholar
[Kn] Knutson, A., The symplectic and algebraic geometry of Horn's problem. Linear Algebra Appl. 319(2000), no. 1-3, 61–81.Google Scholar
[Lo] Loos, O., Symmetric Spaces. II. Compact Spaces and Classification. W. A. Benjamin, New York, 1969.Google Scholar
[LR91] Lu, J. H. and Ratiu, T., On the nonlinear convexity theorem of Kostant. J. Amer. Math. Soc. 4(1991), no. 2, 349–363.Google Scholar
[Mo] Morita, S., Geometry of Differential Forms. Translations of Mathematical Monographs 201, American Mathematical Society, Providence, RI, 2001.Google Scholar
[MW] Meinrenken, E. and Woodward, C., Cobordism for Hamiltonian loop group actions and flat connections on the punctured two-sphere. Math. Z. 231(1999), no. 1, 133–168.Google Scholar
[Ni] Nicas, A. J., Classifying pairs of Lagrangians in a Hermitian vector space. Topology Appl. 42(1991), no. 1, 71–81.Google Scholar
[OS] O’Shea, L. and Sjamaar, R., Moment maps and Riemannian symmetric pairs. Math. Ann. 317(2000), no. 3, 415–457.Google Scholar
[Sc1] Schaffhauser, F., Un théorème de convexité réel pour les applications moment à valeurs dans un group de lie. http://arXiv.org/abs.math.SG/0609517. Google Scholar
[Sc2] Schaffhauser, F., Decomposable representations and Lagrangian submanifolds of moduli spaces associated to surface groups. Ph.D. thesis, Université Pierre et Marie Curie-Paris 6, 2005 http://www.institut.math.jussieu.fr/theses/2005/schaffhauser. Google Scholar
[SL] Sjamaar, R. and Lerman, E., Stratified symplectic spaces and reduction. Ann. of Math. 134(1991), no. 2, 375–422.Google Scholar
[Tr] Treloar, T., The symplectic geometry of polygons in the 3-sphere. Canad. J. Math. 54(2002), no. 1, 30–54.Google Scholar