Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T20:30:50.708Z Has data issue: false hasContentIssue false
  • English
  • Français

A Regular Singular Functional

Published online by Cambridge University Press:  20 November 2018

A. D. Martin
A. D. Martin*
Affiliation:
Washington University, St. Louis and Institute for Advanced Study
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. In a joint paper with Leighton (2), the author considered quadratic functionals of the type

1.1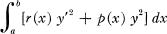 (0 < a < b)

in which x = 0 is a singular point of the functional which is otherwise regular on [0, b]. The hypothesis on a regular functional includes the assumption that r is continuous and positive on a closed interval [0, b].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 8 , 1956 , pp. 53 - 68
Copyright
Copyright © Canadian Mathematical Society 1956

References

1. Leighton, Walter, Principal quadratic functionals, Trans. Amer. Math. Soc, 67 (1949), 253–274.Google Scholar
2. Leighton, Walter and Martin, A. D., Quadratic functionals with a singular endpoint, Trans. Amer. Math. Soc, 78 (1955), 98–128.Google Scholar
3. Morse, Marston, The calculus of variations in the large (Amer. Math. Soc. Colloquium Publications, 18, New York, 1934).Google Scholar
4. Morse, Marston and Leighton, Walter, Singular quadratic functionals, Trans. Amer. Math. Soc, 40 (1936), 252–286.Google Scholar
5. Morse, Marston and Transue, William, A characterization of the bilinear sums associated with the classical second variation, Annali Matematica (4), 28 (1949), 25–68.Google Scholar