Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T06:30:17.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Proof, Disproof and Advances Concerning Certain Conjectures on Real Quadratic Fields

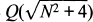
Published online by Cambridge University Press:  20 November 2018

R. A. Mollin  and
H. C. Williams
R. A. Mollin
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta, T2N1N4 e-mail: [email protected]
H. C. Williams
Affiliation:
Computer Science Department, University of Manitoba, Winnipeg, Manitoba, R3T 2N2 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to address conjectures raised in [2]. We show that one of the conjectures is false and we advance the proof of another by proving it for an infinite set of cases. Furthermore, we give hard evidence as to why the conjecture is true and show what remains to be done to complete the proof. Finally, we prove a conjecture given by S. Louboutin, for Mathematical Reviews, in his discussion of the aforementioned paper.

Keywords

11R1111R2911J70
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 5 , 01 October 1995 , pp. 1023 - 1036
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Hecke, E., Eine neue art von Zetafunctionen und ihre Beziehungen zur Verteilung der Primzahlen,, Math. Z. 6(1920), 11–51.Google Scholar
2. Leu, M.G., On a Criterion for the Quadratic Fields to be of Class Number Two, Bull. London Math. Soc. 24(1992), 309–312.Google Scholar
3. Leu, M.G., On a Problem of Ono and quadratic Non-Residues, Nagoya Math. J. 115(1989), 185–198.Google Scholar
4. Mollin, R.A., Class Number One Criteria for Real Quadratic Fields I, Proc. Japan Acad. Ser. A 63(1987), 121–125.Google Scholar
5. Mollin, R.A. and Williams, H.C., Prime-Producing quadratic Polynomials and Real Quadratic Fields of Class Number One. In: Number Theory (ed. Dekoninck, J.M. and Levesque, C.), Walter de Gruyter, Berlin, 1989. 654–663.Google Scholar
6. Mollin, R.A., Solution of the Class Number One Problem for Real Quadratic Fields of Extended Richaud- Degert Type (with one possible exception). In: Number Theory (ed. Mollin, R.A.), Walter de Gruyter, Berlin, New York, 1990. 417–425.Google Scholar
7. Mollin, R.A., On a Solution of a Class Number Two Problem for a Family of Real Quadratic Fields. In: Computational Number Theory, (ed. Pethö, A. et al), Walter de Gruyter, Berlin, New York, 1991. 95–101.Google Scholar
8. Mollin, R.A., A Conjecture of S. Chowla Via the Generalized Riemann Hypothesis, Proc. Amer. Math. Soc. 102(1988), 794-796.Google Scholar
9. Mollin, R.A., Computation of the Class Number of a Real Quadratic Field, Utilitas Math. 41(1992), 259–308.Google Scholar
10. Mollin, R.A., On Real Quadratic Fields of Class Number Two, Math. Comp. 59(1992), 625–632.Google Scholar
11. Mollin, R.A., On a Determination of Real Quadratic Fields of Class Number One and Related Continued Fraction Period Length Less Than 25, Proc. Japan Acad. Ser. A. 67(1991), 20–25.Google Scholar
12. Mollin, R.A., Classification and Enumeration of Real Quadratic Fields Having Exactly One Non-Inert Prime Less Than a Minkowski Bound, Canad. Math. Bull. 36(1993), 108–115.Google Scholar
13. Mollin, R.A. and van, A.J. der Poorten, A note on symmetry and Ambiguity, Bull. Austral. Math. Soc, to appear.Google Scholar
14. Mollin, R.A., Zhang, L.-C. and Kemp, P., A Lower Bound For the Class Number of a Real Quadratic Field of ERD-type, Canad. Math. Bull. 37(1994), 90–96.Google Scholar
15. Tatuzawa, T., On a Theorem ofSiegel, Japan J. Math. 21(1951), 163–178.Google Scholar
16. Williams, H.C. and Wunderlich, M.C., On the Parallel Generation of the Residue for the Continued Fraction Factoring Algorithm, Math. Comp. 177(1987), 405–423.Google Scholar