Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T20:41:04.703Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointed Torsors

Published online by Cambridge University Press:  20 November 2018

J. F. Jardine
J. F. Jardine*
Affiliation:
Mathematics Department, University of Western Ontario, London, ON N6A 5B7 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper gives a characterization of homotopy fibres of inverse image maps on groupoids of torsors that are induced by geometric morphisms, in terms of both pointed torsors and pointed cocycles, suitably defined. Cocycle techniques are used to give a complete description of such fibres, when the underlying geometric morphism is the canonical stalk on the classifying topos of a profinite group 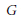$G$. If the torsors in question are defined with respect to a constant group 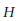$H$, then the path components of the fibre can be identified with the set of continuous maps from the profinite group 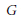$G$ to the group 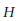$H$. More generally, when 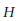$H$ is not constant, this set of path components is the set of continuous maps from a pro-object in sheaves of groupoids to 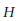$H$, which pro-object can be viewed as a “Grothendieck fundamental groupoid”.

Keywords

18G5014F3555B30pointed torsorspointed cocycleshomotopy fibres
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 6 , 01 December 2011 , pp. 1345 - 1363
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Revêtements étales et groupe fondamental. Exposés I à XIII. Séminaire de géométrie algébrique du Bois Marie 1960/61 (SGA 1), dirigé par Alexander Grothendieck. Augmenté de deux exposés de M. Raynaud. Lecture Notes in Mathematics, 224, Springer-Verlag, Berlin-New York, 1971.Google Scholar
[2] Friedlander, E. M., Étale homotopy of simplicial schemes. Annals of Mathematics Studies, 104, Princeton University Press, Princeton, NJ, 1982.Google Scholar
[3] Goerss, P. G. and Jardine, J. F., Localization theories for simplicial presheaves. Canad. J. Math. 50(1998), no. 5, 1048–1089. doi:10.4153/CJM-1998-051-1Google Scholar
[4] Goerss, P. G. and Jardine, J. F., Simplicial homotopy theory. Progress in Mathematics, 174, Birkhäuser Verlag, Basel, 1999.Google Scholar
[5] Hovey, M., Model categories. Mathematical Surveys and Monographs, 63, American Mathematical Society, Providence, RI, 1999.Google Scholar
[6] Jardine, J. F., Simplicial presheaves. J. Pure Appl. Algebra 47(1987), no. 1, 35–87. doi:10.1016/0022-4049(87)90100-9Google Scholar
[7] Jardine, J. F., Generalized étale cohomology theories. Progress in Mathematics, 146, Birkhäuser Verlag, Basel, 1997.Google Scholar
[8] Jardine, J. F., Cocycle categories. In: Algebraic topology, Abel Symp., 4, Springer, Berlin, 2009, pp. 185–218.Google Scholar
[9] Milne, J. S., Étale cohomology. Princeton Mathematical Series, 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar