Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-08T05:32:24.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Outer Derivations and Classical-Albert-Zassenhaus lie Algebras

Published online by Cambridge University Press:  20 November 2018

David J. Winter
David J. Winter*
Affiliation:
University of Michigan, Ann Arbor, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the structure of the derivation algebra Der L of the Lie algebra L with split Cartan subalgebra H. The Fitting decomposition

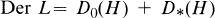
of Der L with respect to ad ad H leads to a decomposition

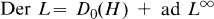
where

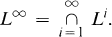
This decomposition is studied in detail in Section 2, where the centralizer of ad L∞ in D0(H) is shown to be

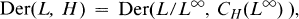
which is Hom(L/L2, Center L) when H is Abelian. When the root-spaces La (a nonzero) are one-dimensional, this leads to the decomposition of Der L as

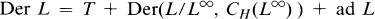
where T is any maximal torus of D0(H).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 6 , 01 December 1984 , pp. 961 - 972
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Albert, A. A. and Frank, M. S., Simple Lie algebras of characteristic p, Univ. e Politec. Torino, Rend. Sem. Mat. 14 (1954-5), 117–139.Google Scholar
2. Block, R., On Lie algebras of rank 1, Trans. A.M.S. 112 (1964), 19–31.Google Scholar
3. Block, R., On the Mills-Seligman axioms for Lie algebras of classical type, Trans. A.M.S. Soc. 121 (1966), 378–392.Google Scholar
4. Block, R., Trace forms in Lie algebras, Can. J. Math. 14 (1962), 553–564.Google Scholar
5. Mills, W., Classical type Lie algebras of characteristics 5 and 7, J. Math. Mech. 6 (1957), 559–566.Google Scholar
6. Mills, W. and Seligman, G., Lie algebras of classical type, J. Math. Mech. 6 (1957), 519–548.Google Scholar
7. Schenkman, E., A theory of subinvariant Lie algebras, Am. J. Math. 173 (1951), 453–474.Google Scholar
8. Seligman, G., Modular Lie algebras, Ergebnisse der Math. u. ihrer Grenzegebiete Bd. 40 (Springer-Verlag, Berlin, 1967).CrossRefGoogle Scholar
9. Winter, D. J., On the toral structure of Lie p-algebras, Acta Math. 123 (1969), 70–81.Google Scholar
10. Winter, D. J., Symmetric Lie algebras. CrossRefGoogle Scholar
11. Winter, D. J., Symmetrysets, J. of Alg. 73 (1981), 238–247.Google Scholar