Hostname: page-component-66644f4456-kglw6 Total loading time: 0 Render date: 2025-02-12T16:03:53.861Z Has data issue: true hasContentIssue false
  • English
  • Français

Ordered Groups Satisfying the Maximal Condition Locally

Published online by Cambridge University Press:  20 November 2018

R. J. Hursey  and
A. H. Rhemtulla
R. J. Hursey
Affiliation:
East Carolina University, Greenville, North Carolina
A. H. Rhemtulla
Affiliation:
The University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 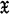denote the class of all (fully) ordered groups satisfying the maximal condition on subgroups, and let 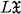denote the class of all locally 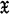groups. In this paper we investigate the family of convex subgroups of 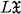groups.

It is well known (see [1, pp. 51, 54]) that every convex subgroup of an 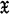is normal in G, and for any jump D –< C in the family of convex subgroups, [G′, C] ⊆ D. We observe that these properties are also true for any 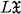group and record, without proof, the following.

THEOREM 1. Any convex subgroup of an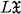group G is normal in G, and for any jump D –< C in the family of convex subgroups, [G′, C] ⊆ D.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 753 - 758
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Fuchs, L., Partially ordered algebraic systems (Addison-Wesley, Reading, Massachusetts, 1963).Google Scholar
2. Neumann, B. H., On ordered groups, Amer. J. Math. 71 (1949), 1–18.Google Scholar
3. Ree, R., On ordered, finitely generated, solvable groups, Trans. Roy. Soc. Canada (3) 48 (1954), 39–42.Google Scholar
4. Ree, R., The existence of outer automorphisms of some groups. II, Proc. Amer. Math. Soc. 9 (1958), 105–109.Google Scholar
5. Teh, H. H., Construction of orders in abelian groups, Proc. Cambridge Philos. Soc. 57 (1961) 476–482.Google Scholar