Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T16:09:54.105Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Tensor Products of JW-Algebras

Published online by Cambridge University Press:  20 November 2018

Fatmah B. Jamjoom
Fatmah B. Jamjoom*
Affiliation:
Department of Mathematics, King Saud University, Riyadh, Saudi Arabia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we introduce and develop a theory of tensor products of JW-algebras. Since JW-algebras are so close to W*-algebras, one can expect that the W*-algebra tensor product theory will be actively involved. It is shown that if Mand N are JW-algebras with centres Z1 and Z2 respectively, then Z1 ⊗ Z2 is not the centre of the JW-tensor product JW(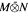) (see below for notation) ofMand N, in general. Also, the type decomposition of JW(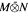) has been determined in terms of the type decomposition of the JW-algebras M and N which, essentially, rely on the relationship between the types of the JW-algebra and the types of its universal enveloping Von Neumann algebra.

Keywords

46L1046L0546D25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 4 , 01 August 1995 , pp. 786 - 800
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Ajupov, S.A., Extensions of traces and type criterions of Jordan algebras of self-adjoint operators, Math. Z. 181(1982), 253–268.Google Scholar
2. Alfsen, E.M., W, F. Shultz and Hanche-Olsen, H., State spaces of C -algebras, Acta Math. 144(1980), 267–305.Google Scholar
3. Bunce, L.J. and Wright, J.D.W., Introduction to the K-theory of Jordan C*-algebras, Quart. J. Math. Oxford Ser. (2) 40(1989), 377–398.Google Scholar
4. Jamjoom, F., The connection between the universal enveloping C* -algebra and the universal enveloping Von Neumann algebra of a W-algebra, Math. Proc. Cambridge Philos. Soc. 112(1992), 575–579.Google Scholar
5. Jamjoom, F., On the tensor products ofiC-algebras, Quart. J. Math. Oxford Ser. (2) 45(1994), 77–90.Google Scholar
6. Jamjoom, F., On the tensor product of simple JC-algebras, Michigan Math. J. 41(1994), 289–295.Google Scholar
7. Gil, J. de Lamadrid, Measures and tensors, Trans. Amer. Math. Soc. 127(1967), 312–315.Google Scholar
8. Hanche-Olsen, H., On the structure and tensor products of JC-algebras, Canad. J. Math. 35(1983), 1059–1074.Google Scholar
9. Hanche-Olsen, H. and Stormer, E., Jordan operator algebras, Pitman, 1984.Google Scholar
10. Jacobson, N., Structures and representations of Jordan algebras, Amer. Math. Soc. Colloq. Publ. 39, Providence, 1968.Google Scholar
11. Kadison, R.V. and Ringrose, J.R., Fundamentals of the theory of operator algebras II, Academic Press, 1986.Google Scholar
12. Karoubi, M., K-Theory, Springer-Verlag, 1978.Google Scholar
13. Pedersen, G.K., C* -algebras and their automorphism groups, Academic Press, 1979.Google Scholar
14. Sakai, S., On the tensor product of W*-algebras, Amer. J. Math. 90(1968), 335–341.Google Scholar
15. Sakai, S., C* -algebras and W* -algebras, Springer-Verlag, 1971.Google Scholar
16. Stacey, P.J., The structure of Type IJWN-algebras, Math. Proc. Cambridge Philos. Soc. 90(1981), 477–482.Google Scholar
17. Stacey, P.J., Type h JBW-algebras, Quart. J. Math. Oxford (2) 33(1982), 115–127.Google Scholar
18. Stormer, E., On the Jordan structure of C*-algebras, Trans. Amer. Math. Soc. 120(1965), 438–447.Google Scholar
19. Stormer, E., Irreducible Jordan algebras of self adjoint operators, Trans. Amer. Math. Soc. 130(1968), 153–166.Google Scholar
20. Takesaki, M., Theory of operator algebras I, Springer-Verlag, 1979.Google Scholar
21. Topping, D.M., Jordan algebras of self adjoint operators, Mem. Amer. Math. Soc. 53(1965).Google Scholar